Вывод формул для определения градиентов ошибок на входе выходного нейрона и нейрона j скрытого слоя n.
(3
)
где под yj, подразумевается выход нейрона j, а под sj– взвешенная
сумма его входных сигналов (PSP), т. е. аргумент активационной функции. Так как множитель dyj /dsj является производной этой функции по ее
аргументу, следовательно, производная активационной функции должна быть определена на всей оси абсцисс. Поэтому функция единичного
скачка и прочие активационные функции с неоднородностями не подходят для рассматриваемой нейронной сети и данной методики обучения. Как правило, применяются такие гладкие функции, как гиперболическая или
логистическая. В случае гиперболического тангенса:
(4
)
В случае логистической функции:
(5
)
Третий множитель |
в формуле 3 равен выходу |
нейрона |
предыдущего слоя :
(6
)
Первый множитель формулы 3 раскладывается следующим образом:
, |
(7 |
|
) |
где суммирование по k выполняется среди нейронов слоя n+1 и :
(8
)
Введем переменную |
, |
(9 |
|
|
|
|
|
) |
которая называется градиентом ошибки на входе нейрона j слоя n.
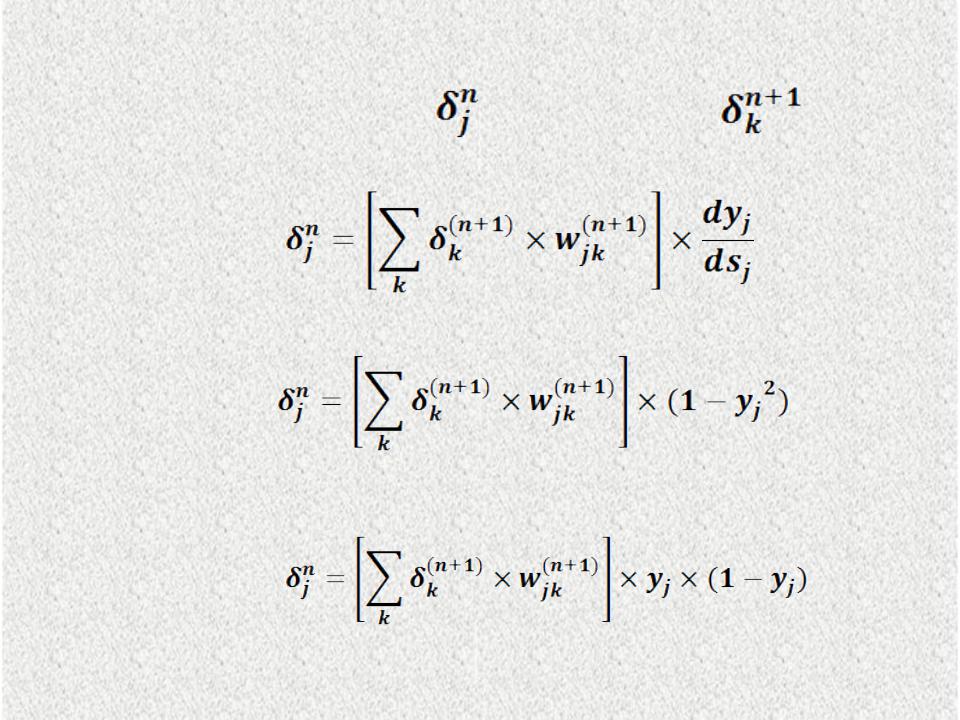
Подставляя в формулу 9 вторую часть формулы 7, получим рекурсивную
формулу для расчётов величин |
слоя n из величин |
более |
старшего слоя n+1 : |
|
|
(10
)
С учётом формул 4 и 5 получим при гиперболической функции активации нейрона j слоя n:
(11
)
при логистической функции активации нейрона j слоя n:
(12
)
Для выходного слоя при гиперболической функции активации нейрона:
(13
)
Для выходного слоя при логистической функции активации нейрона:
(14
)
где L - номер нейрона в выходном слое.
Подставляя выражения 9 и 6 в формулу 3, а выражение 3 в формулу 1 (формулу для приращения веса), получим формулу 1 в виде:
(15
)
Для придания процессу коррекции весов инерционности, сглаживающей резкие скачки при перемещении по поверхности целевой функции, формула 15 дополняется значением изменения веса на предыдущей итерации:
(16
)
Пошаговое описание алгоритма обратного распространения ошибок
Рассматриваем нейронную сеть рис.4. Считаем, что все нейроны имеют
логистическую функцию активации.
Шаг 1. Весам сети присваиваются небольшие начальные значения, например значениями из диапазона между -0.3 и +0.3, полученные с помощью генератора случайных чисел, распределённых по нормальному, равномерному или иному закону.
Шаг 2. Выбирается очередная обучающая пара (X,Y) из обучающего множества; вектор X подаётся на вход сети. C каждым входным образцом X связывается целевой выходной образец Y.
Шаг 3. Вычисляется результат на каждом j-м выходе сети.
Шаг 4. Вычисляется разность между требуемым d (целевым Y) и реальным y (вычисленным) выходом сети, т.е. каждый из выходов сети вычитается из соответствующего компонента целевого вектора (выходного образца) с целью получения ошибки. После этого вычисляется локальный градиент ошибки для каждого элемента сети, кроме входных. Для выходных элементов используется формула (14):
а для элементов внутренних слоёв – формула (12):
Шаг 5. Веса сети корректируются так, чтобы минимизировать ошибку (формула 2). Вычисление приращения веса выполняется по формуле (16):
Если момент инерции выбрать равным 0, то формула 16 переходит в формулу 15:
Таким образом, новый вес на шаге t определяется как сумма веса на шаге (t-1) и приращения на шаге t:
wij t wij t wij (t 1)
(17
)
Шаги со 2-го по 5-й повторяются для каждой пары тренировочного множества до тех пор, пока не выполнится условие останова. . Например, обучение продолжается до тех пор, пока изменение квадратичной ошибки не окажется меньше некоторого допустимого значения при переходе от одной эпохи к следующей (или не выполнится другое условие останова). Шаги 2 и 3 можно рассматривать как «проход вперёд», так как сигнал распространяется по сети от входа к выходу. Шаги 4 и 5 составляют «обратный проход», поскольку здесь вычисляемый сигнал ошибки распространяется обратно по сети и используется для подстройки весов.
2
3
1
-1
Прямой
проход
-1 |
0.99606 |
|
7 |
||
|
||
|
5.532739 |
23
Целевым является |
значение |
0.8, |
|
||
поэтому |
ошибка для выходного |
||||
элемента |
равна |
|
|
|
|
(0.800 - 0.99606) x |
0.99606 |
|
|
||
x (1 - 0.99606) = -0.00077 |
|
|
|||
|
|
-1 |
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-0.00077 |
|
|
Ошибка предыдущего |
|
|
|
|
|
|
|
|
|
|
|
слоя, умноженная на |
|
2 |
|
3 |
|
весовые значения |
|
|
|||
0.778713 0.991771 
5 6 
1.258181 4.791865
1 |
2 |
0,598688 |
0,731059 |
3 |
4 |
0.4 |
1 |
22
0.2 |
0.8 |
1 |
2 |
-2 |
2 |
Фактическая ошибка 
0.778713 x(1- 0.778713 ) x -0.00154
3 |
3 |
1 |
1 |
2 |
-1 |
|
-0.00154 |
-0.00231 |
5 |
6 |
-0.00027 |
-0.000019 |
1 |
2 |
-0.00083 |
-0.0006 |
3 |
4 |
-0.0002 |
-0.00012 |
2 |
2 |
0.2 |
0.8 |
1 |
2 |
-2
3
1
2
Входные элементы с линейной функцией активации передают входной сигнал
на свои выходы без изменений. Они также не имеют порогов. Совокупный входной |
||||||
сигнал будем считать по формуле . |
|
n |
|
|
||
s j |
xi |
wij |
w0 j |
|||
|
|
|||||
Для третьего элемента w(0,3)=1, w(1,3)=-1, w(2,3)=2, i 1 |
|
|
||||
S3 |
= (-1*0.2) + (2*0.8) - (1*1) = 0.4 |
|
|
|
|
|
Выходной сигнал третьего элемента рассчитаем по формуле (2) |
|
|||||
Y3 |
= 1/(1 + exp(-0.4))= 0,598688 |
|
|
|
|
|
Выполним подобные вычисления для остальных элементов сети |
|
|||||
S4 |
= (2 * 0.2) + (2 * 0.8) - (1*1) = 1 |
|
|
|
|
|
Y4 |
= 1/(1+exp(-3)) = 0,731059 |
|
|
|
|
|
S5 |
= (3 * 0,598688) + (2 * 0,731059 ) - (2 * 1) = 1.258181 |
|
|
|||
Y5 |
= 1/(1+exp(- 1.258181)) = 0.778713 |
|
|
|
|
|
S6 |
= (1 * 0,598688) + (3 * 0,731059 ) - (-2*1) = 4.791865 |
|
|
|||
Y6 |
= 1/(1+exp(- 4.791865)) = 0.991771 |
|
|
|
|
|
S7 |
= (2* 0.778713 ) + (3 * 0.991771) - ( -1*1) = 5.532739 |
|
|
|||
Y7 |
= 1/(1+exp(- 5.532739)) = 0.99606 |
|
|
|
|
|
Градиент ошибки выходного элемента рассчитаем по формуле (14) δ7 = 0.99606 * (1 – 0.99606) * (0.8 – 0.99606) = -0.00077.
Градиенты ошибок скрытых элементов рассчитаем по формуле (12) δ6 = 0.991771 * (1 – 0.991771 ) * (3 * - 0.00077) = -0.000019 δ5 = 0.778713 * (1 – 0.778713 ) * (2*- 0.00077) = -0.00027
δ4 = 0.731059*(1- 0.731059)*(2* -0.00027 +3*- 0.000019) = -0.00012 δ3 = 0.598688*(1- 0.598688)*(3*-0.00027+1*-0.000019) = -0.0002
Вычислим значения приращений весовых коэффициентов по формуле (15), когда момент инерции µ равен нулю. Такая ситуация характерна для первого образца из обучающей выборки, поскольку для этого образца нет изменения предыдущего веса.
Δw(0,7) = 0.07 * (-0.00077) = -0.0000539
Δw(5,7) = 0.07 * (-0.00077) * 0.778713 = -0.000042 Δw(6,7) = 0.07 * (-0.00077) * 0.991771 = -0.000053 Δw(0,6) = 0.07 * (-0.000019) * 1 = -0.000001
Δw(3,6) = 0.07 * (-0.000019) * 0.598688 = -0.00000008 Δw(4,6) = 0.07 * (-0.000019) * 0.731059 = -0.00000001 Δw(0,5) = 0.07 * (-0.00027) * 1 =- 0.0000019
Δw(3,5) = 0.07 * (-0.00027) * 0.598688 = -0.000011 Δw(4,5) = 0.07 * (-0.00027) * 0.731059 = -0.000014 Δw(0,4) = 0.07 * (-0.00012) * 1 = -0.0000084 Δw(1,4) = 0.07 * (-0.00012) * 0.2 = -0.0000017 Δw(2,4) = 0.07 * (-0.00012) * 0.8 = -0.0000067 Δw(0,3) = 0.07 * (-0.0002) * 1 = -0.000014
Δw(1,3) = 0.07 * (-0.0002) * 0.2 = -0.0000028 Δw(2,3) = 0.07 * (-0.0002) * 0.8 = -0.000011
Вычислим новые значения весовых коэффициентов по формуле (17)
w(0,7) = -1 + -0.0000539 = -1.0000539 w(5,7) = 2 + -0.000042 = 1.999958 w(6,7) = 3 + -0.000053 = 2.999947 w(0,6) = -2 + -0.000001 = -2.000001 w(3,6) = 1 + -0.00000008 = 0.99999992 w(4,6) = 3 + -0.00000001 = 2.99999999 w(0,5) = 2 + - 0.0000019 = 1.9999981 w(3,5) = 3 + -0.000011 = 2.999989 w(4,5) = 2 + -0.000014 = 1.999986 w(0,4) = 1 + -0.0000084 = 0.999986 w(1,4) = 2 + -0.0000017 = 1.9999972 w(2,4) = 2 + -0.0000067 = 1.9999983 w(0,3) = 1 + -0.000014 = 0.999986 w(1,3) = -1 + -0.0000028 = -1.0000028 w(2,3) = 2 + -0.000011 = 1.999989