лица 2. 1.Виды активационных функций F
Название
линейная
полулинейная
логистическая
(сигмоидальная)
гиперболический тангенс (сигмоидальная)
Экспоненциальная
Синусоидальная
Сигмоидальная
(рациональная)
Шаговая (линейная с насыщением)
Пороговая
функция
f(s)= ks
f(s)= ks , s > 0 f(s)= 0 , s <= 0
f(s)= 1/(1+e-as)
f(s)= (eas-e-as) / (eas+e-as)
f(s) = e-as f(s) = sin(s)
f(s) = s / (a+|s|)
f(s) = -1, s <= -1 f(s) = 0, -1 < s < 1 f(s) = 1, s >= 1
f(s) = 0, s < 0 f(s) = 1, s >= 0
Область
значений (- )
(0, )
(0,1)
(-1,1)
(0, )
(-1,1)
(-1,1)
(-1,1)
(0,1)
Продолжение таблицы 2.1. Виды активационных функций F
Название |
функция |
Область |
|
значений |
|||
|
|
Модульная |
f(s) = |s| |
(0, |
Знаковая |
f(s) = sgn(s), s!=0 |
(-1,1) |
|
(сигнатурная) |
f(s) = -1, s = 0 |
||
|
Квадратичная |
f(s) = s2 |
|
|
|
(-1,1) |
||||
|
|
|
|
|
|
( X |
|
) |
|
|
f (s) |
2 e |
X |
|
|||||
|
|
|
|
|
|||||
Радиально-базисная |
|
|
1 |
|
|
2 2 |
(-∞,∞) |
||
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
||
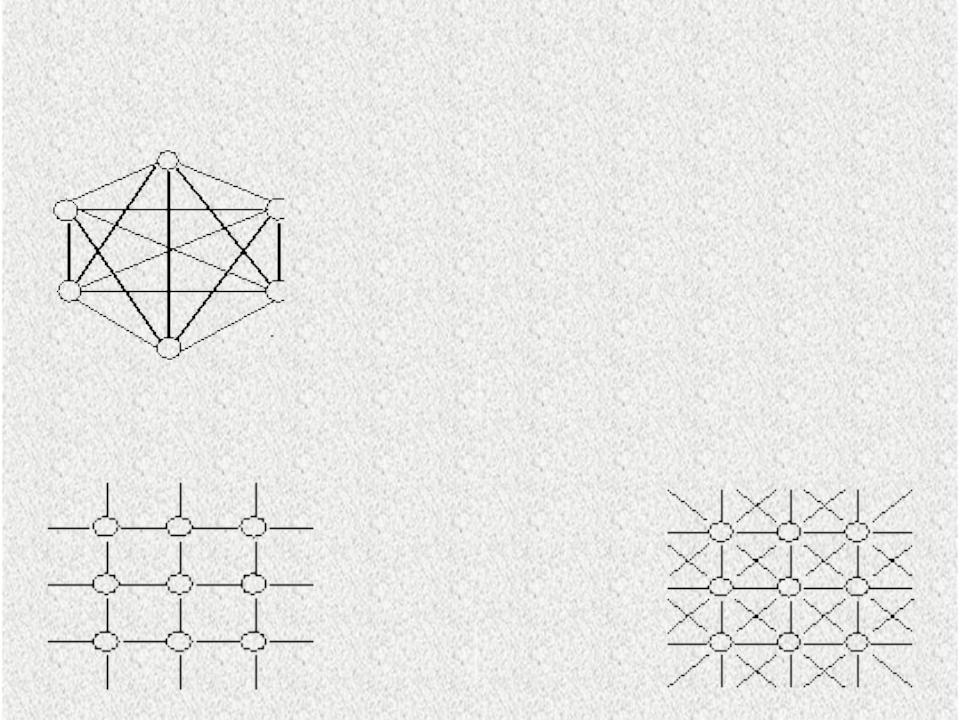
Классификация нейронных сетей
1 Классификация по количеству связей и тополог
1.1 Полносвязанная сеть. Каждый нейрон передает свой выходной сигнал всем остальным нейронам в сети, включая самого себя.
1.2 Неполносвязанные сети разделяются по топологии: 1.2.1 Сети без обратных связей:
1.2.1.1Слабосвязанные сети:
Вслабосвязанных сетях нейроны
располагаются в узлах прямоугольной или
гексагональной
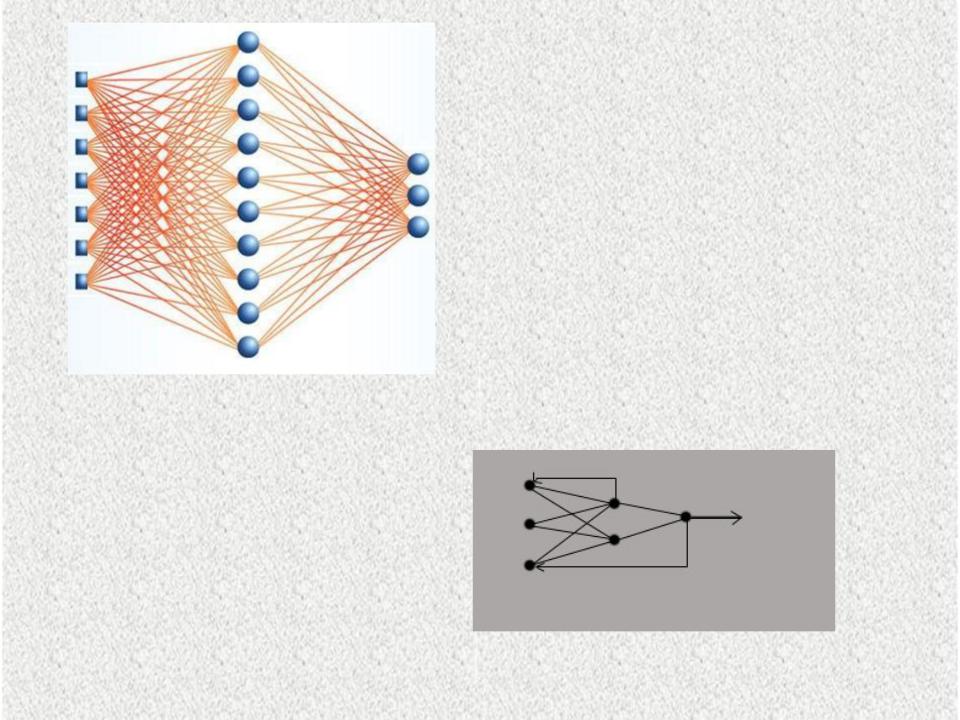
1.2.2.2 Сети прямого распространения:
1.2.1 Сети с обратными связями (рекуррентные):
№2 Классификация по типам структур:
2.1 Гомогенные: |
2.2 Гетерогенные |
Нейроны одного типа |
|
с единой функцией активации. |
Нейроны с различными функциями |
|
активации. |
№3 Классификация по типу сигнала:
Бинарные - двоичный сигнал |
Аналоговые. |
№4 Классификация по типу работы
4.1 Синхронные |
4.2 Асинхронные |
В момент времени t, лишь один |
Группа нейронов |
|
меняет свое состояние. |
нейрон меняет свое состояние. |
Как правило, группа |
|
означает весь слой. |
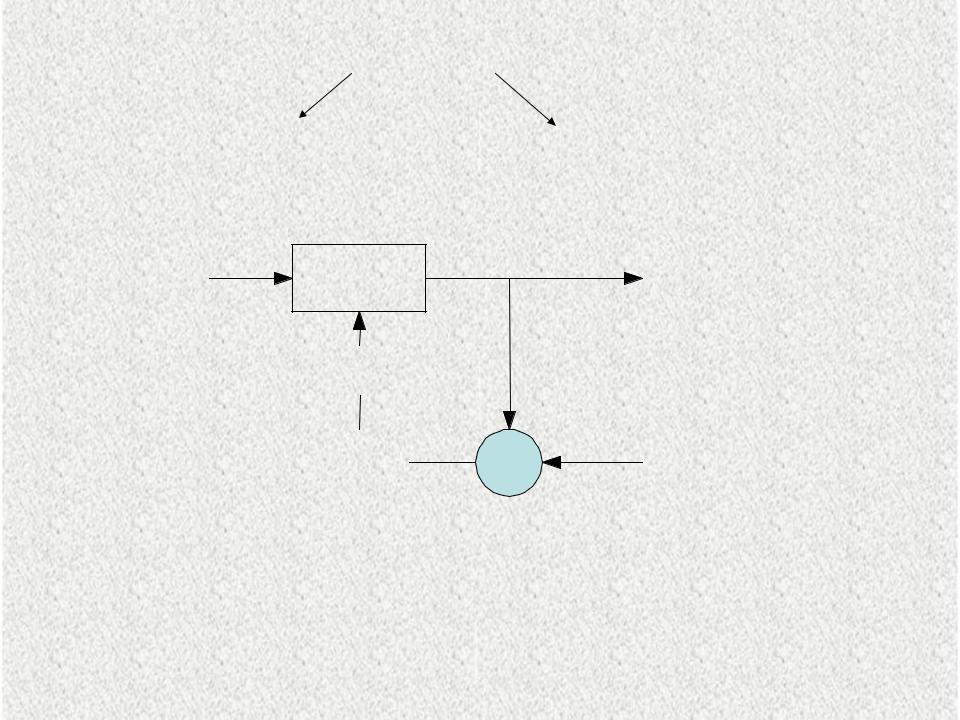
Методы обучения НС делятся на
обучение “с учителем" |
"без учителя" |
Входная |
Нейронная |
Выходной вектор |
|
обучающая |
|||
сеть |
нейронной сети |
||
выборка |
|||
|
|
||
|
Изменение |
|
|
|
весов |
|
|
|
Ошибка |
Известные |
|
|
сети |
значения |
Рис 2.2. Схема обучения НС с учителем
Обучение с учителем предполагает, что для каждого
входного вектора существует целевой вектор, представляющий собой требуемый выход. Вместе они
называются представительской или обучающей выборкой.
Входная |
|
|
|
Выходной |
обучающ |
Нейронная сеть |
|
||
|
вектор |
|||
ая |
|
|
|
|
|
|
|
нейронной |
|
выборка |
|
|
|
|
Параметр |
|
|
сети |
|
|
|
|
||
|
ы сети |
Изменени |
|
|
|
|
|
||
|
|
е весов |
|
|
Ошибка
сети
Рис.2.3 Схема обучения НС без учителя
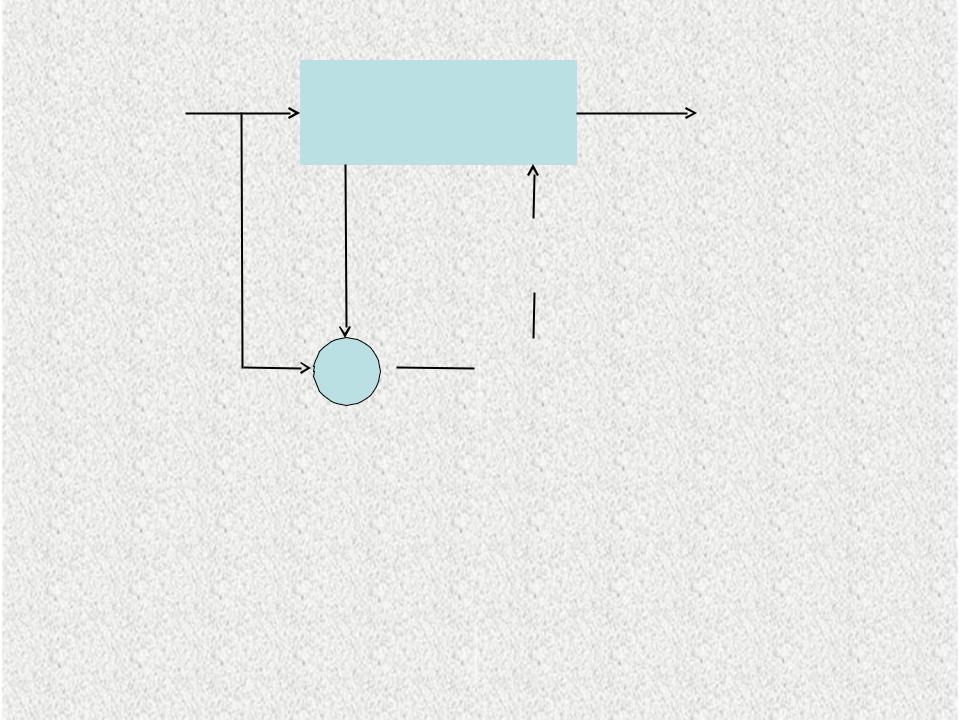
Нейронной сети предъявляются только входные сигналы, а выходы сети формируются самостоятельно с учетом только входных и производных от них сигналов.
Нейронные сети прямого распространения:
1.
ПЕРЦЕПТРОН
Розенблатта
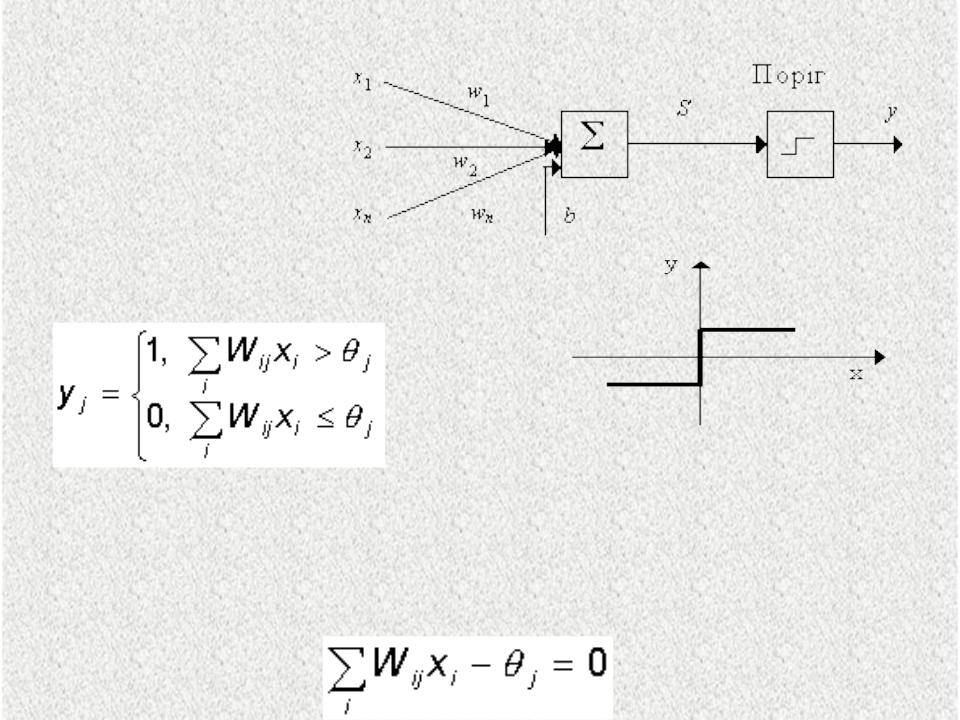
Рис.2.4.Структура перцептрона Розенблатта
Рис.2.5.Функция активации перцептрона Розенблатта
При заданных значениях весов и порогов, нейрон имеет определенное значение выходной активности для каждого возможного вектора входов. Множество входных векторов, при которых нейрон активен (y=1), отделено от множества векторов, на которых нейрон пассивен (y=0) гиперплоскостью, уравнение которой :
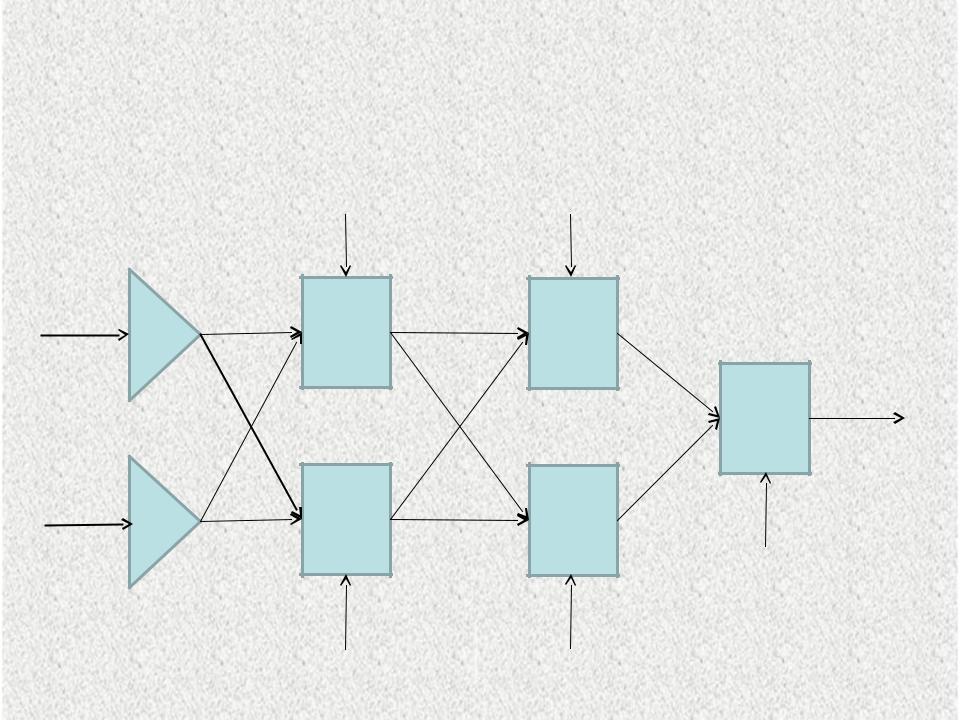
2.Многослойный перцептрон - один из наиболее
распространенных видов нейронных сетей, являющийся многослойной структурой, в которой каждый нейрон произвольного слоя связан со всеми аксонами нейронов предыдущего слоя, или в случае первого слоя нейронов со всеми входами нейронной сети.
X1
X2
W1_h1#
1
W1_h1#
2W2_h1#
1
W2_h1#
2
Wh1#
1Wh1#1_h2#
h1#1 1
Wh1#1_h2#
W2 h1#2_h2#
1
h1#2
Wh1#2_h2#
Wh1#2
Wh2#
1
Wh2#1_3#1
h2#1
Y1
3#1
h2#2 Wh2#2_3#1 W3#1
Wh2#
Рис.2.6. Четырёхслойный перцептрон с двумя2 скрытыми слоями по
2
два нейрона в каждом и одним нейроном в выходном слое.
Методики обучения нейронных сетей
Для обучения нейронной сети необходимо выбрать критерий обучения сети и алгоритм обучения.
Процесс обучения заключается в подборе весов нейронной сети заданной архитектуры. Архитектура нейронной сети определяется её структурой и заданными функциями активации.
Для многослойных перцептронов наиболее распространённым критерием обучения является критерий минимума суммы квадратов ошибок между полученными и целевыми значениями на выходе перцептрона. Наиболее распространённым алгоритмом обучения перцептрона является алгоритм обратного распространения ошибки.
Эта методика обучения нейронной сети относится к методикам градиентного спуска в пространстве ошибок.
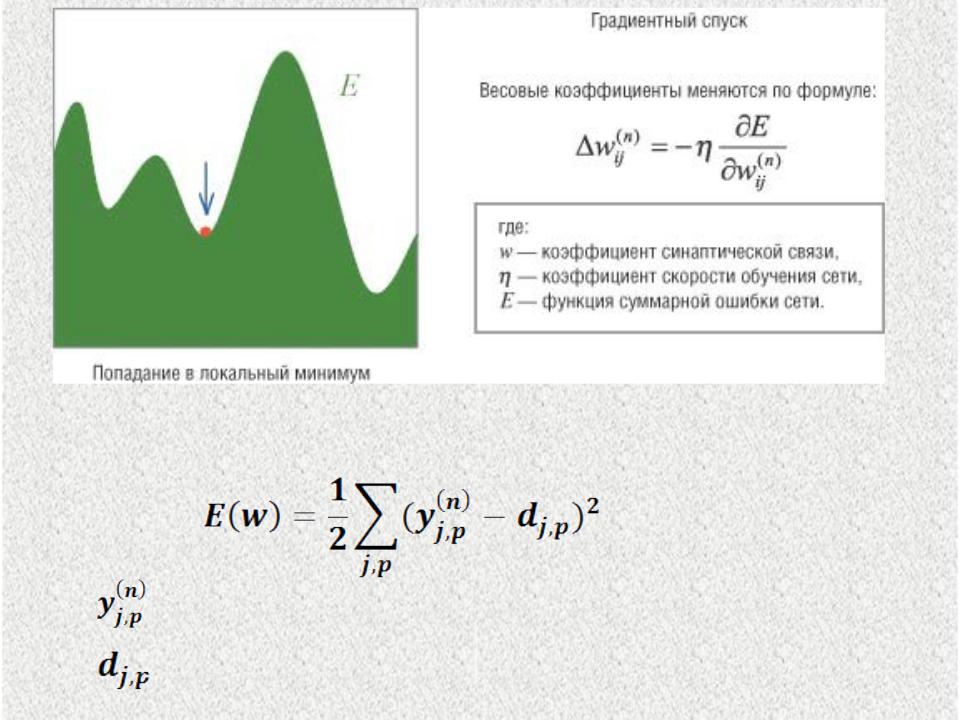
(1
)
Рис.2.7.
Согласно методу наименьших квадратов минимизируемой целевой функцией ошибки нейронной сети является:
(2
)
где реальное выходное состояние j нейрона n –го выходного слоя нейронной сети при подаче на
ее входы p-го образа;
целевое выходное состояние этого нейрона.