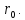Рассмотрим равновесие шатуна ав

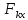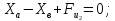
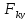∑= 0;

∑= 0;

∑

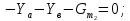
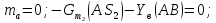
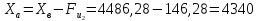
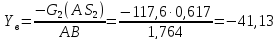
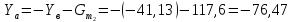
3.4 Определение уравновешивающей силы по методу н.В. Жуковского

Рычагом Жуковского называется повернутый на 90^° план скоростей механизма в данный момент времени. К этому плану нужно приложить все силы которые действуют в одноименных точках реального механизма.

Составляют уравнения моментов всех сил относительно полюса плана скоростей. Сумма моментов должна равняться нулю. Из данного уравнения определяют значение уравновешивающей силы и сравнивают ее со значением полученным при силовом расчете.

Отклонение в результатах должно получиться не более 3%.

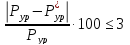
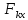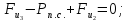
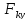∑= 0;

∑= 0;

∑

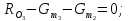
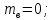
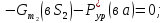
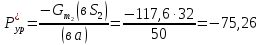
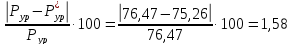
4. Синтез кулачкового механизма

Кулачковым называ­ется механизм, в состав которого входит кулачок. Кулачковые меха­низмы подразделяются по видам движения входных и выходных звеньев, способу замыкания высшей пары, виду элемента высшей пары выходного звена и др.

Задача синтеза кулачковых механизмов заключается в опреде­лении основных размеров и профиля кулачка по заданным кинема­тическим и динамическим параметрам.

Входными параметрами являются: структурная схема механиз­ма; закон движения входного и выходного звеньев; максимальное перемещение выходного звена (линейное h или угловое φ); фазовые углы: удаления φ_у, дальнего стояния φ_д.с, приближения φ_п. Задается также максимальный (допускаемый) угол давления.

4.1 Построение диаграмм движения толкателя. Косинусоидальный закон. Диаграмма перемещения

Строим оси координат s=f(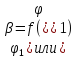. По оси ординат откладываем отрезок h=22 мм, соответствующий максимальному ходу толкателя, а по оси 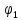отрезки, пропорциональные фазовыми углами 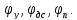Делим эти отрезки на равное число частей (в нашем случае на 8). Проводим полуокружность радиусом

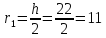мм

и делим ее на 8 равных частей. Из точек деления проводим прямые, параллельные ос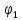и , до пересечения их с соответствующими ординатами.

Диаграмма 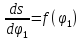. Из начала координат радиусом

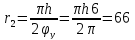мм

проводим четверть окружности, которую делим на 4 равные части. Из точек деления проводим прямые, параллельные оси , до пересечения с соответствующими ординатами. Для фазы приближения построения аналогичные, только радиус другой,

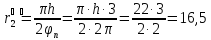мм

Углы 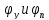в формулы для определения 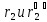подставляют в радианах.

Диаграмма 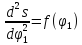. Из начала координат для фазы удаления и из точки 17 для фазы приближения проводим полуокружности радиусами

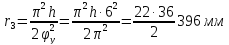
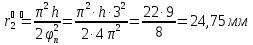
Делим эти полуокружности на 8 равных частей. Точки деления сносим параллельно оси 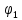до пересечения с соответствующими ординатами. Масштабы всех диаграмм при таких построениях будут одинаковыми и равными, μ_s= 2:1, т.е. 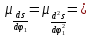μ_s .

4.2 Определение минимального радиуса кулачка

Задано: диаграмма перемещения толкателя s=f(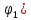, диаграмма второй производной от перемещения толкателя по углу поворота кулачка

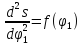, угол давления θ=0. Определить минимальный радиус кулачка .

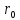Cтроим диаграмму перемещения в функции второй производной от перемещения по углу поворота кулачка, т.е. s=f(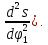Проводим взаимно перпендикулярные оси. Ось ординат обозначим через s, а ось абцисс – через 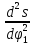. На оси s от начала координат откладываем отрезки (0-1), (0-2) … (0-17), равные ординатам (1-1^*), (2-2^*) … (16-16^*) диаграммы s=f(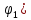. Через точки 1, 2, 3 и т.д. проводим перпендикуляры к оси s. На этих перпендикулярах отложим отрезки (1-1⁰), (2-2⁰) … (16-17⁰), равные ординатам 1-1˝,2-2” … 16-16^˝ диаграммы 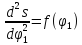. Соединяем полученные точки 1⁰,

2⁰ … 17⁰ плавной кривой. К отрицательной части диаграммы s = f(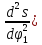 (левый квадрант) проводим касательную под углов 45° до пересечения ее с осью ординат. Получаем точку О ́. Задаемся минимальным радиусом кривизны кулачка. Пусть ρ_min=10 … 15 мм. Отложим ρ_min в масштабе μ_s=2:1 вниз от точки О ́. Получим точку О₁. Тогда расстояние О₁О – есть минимальный радиус кулачка