4. Закон Джоуля-Ленца в интегральной и дифференциальной формах
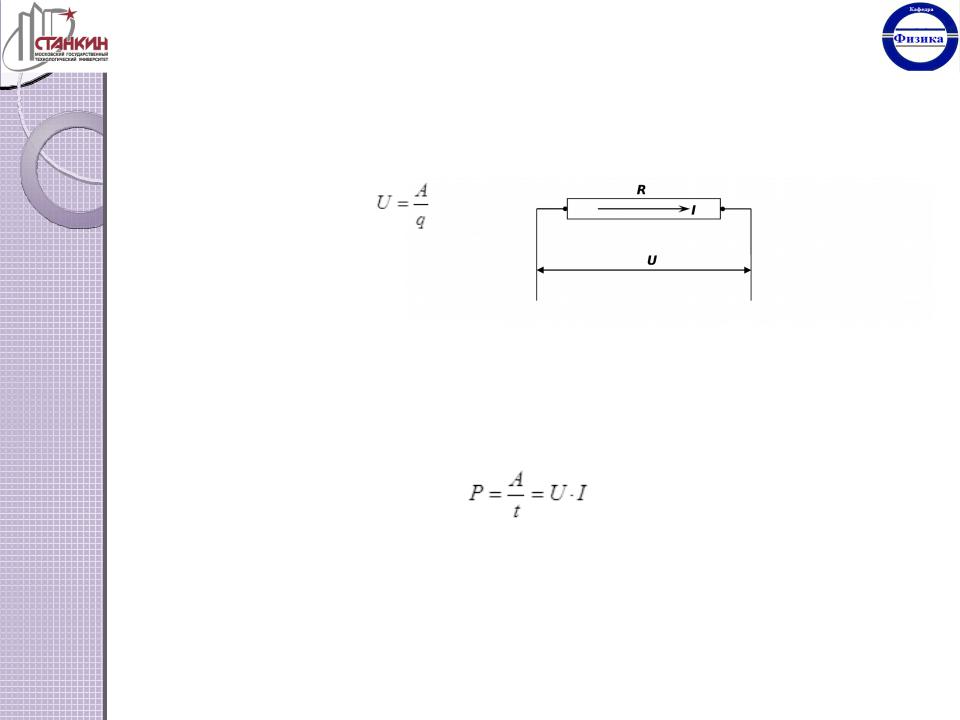
Пусть на участке электрической цепи протекает постоянный ток I (рис. 6.7.). Напряжение U на концах этого участка численно равно работе, совершаемой электрическими силами при перемещении единичного положительного заряда по этому участку:
Рис. 6.7.
Отсюда работа A = q U. За время t по участку будет перенесён заряд q = I t и при этом
будет совершена работа: A = q U = U I t. (6.14)
Это выражение работы электрического тока справедливо для любых проводников.
Работа, совершаемая в единицу времени называется мощностью электрического тока:
В системе СИ мощность измеряется в ваттах:
1 Вт = 1 Дж/1 с = 1 В 1 А.
Если химическое действие и механическая работа при течении тока не производятся, то вся работа электрического тока расходуется только на нагревание проводника:
Q = A = U I t = I2 R t. |
(6.15) |
Закон о тепловом эффекте электрического тока был экспериметально установлен независимо английским учёным Д. Джоулем и русским академиком Э.Х. Ленцем. Формула (6.15) называется законом Джоуля-Ленца в интегральной форме. Она позволяет вычислить количество теплоты, выделяющейся в проводнике.
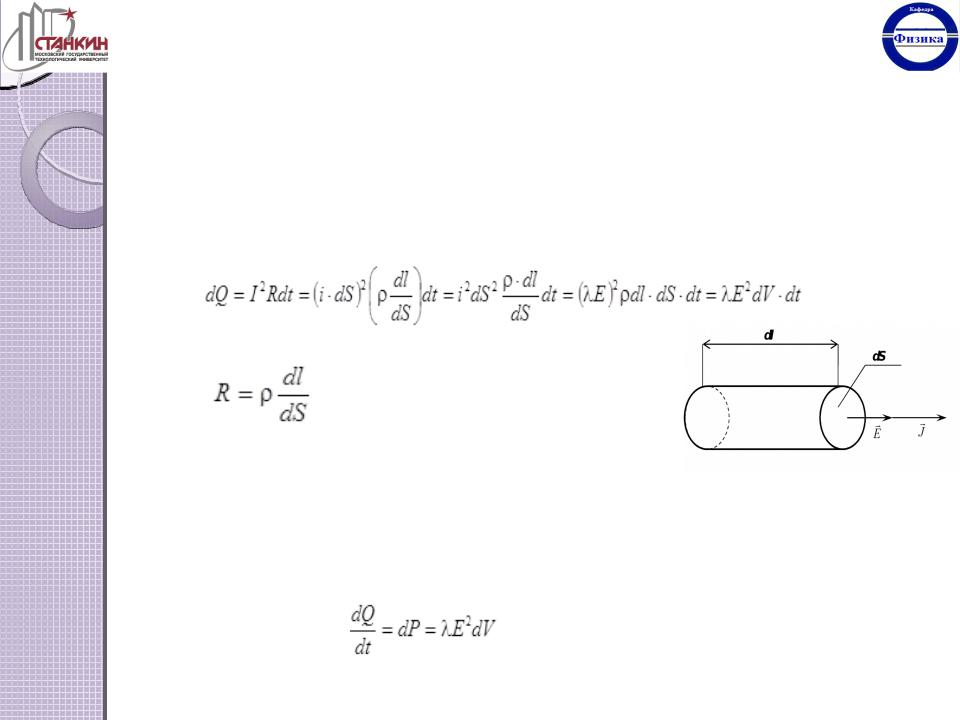
Для того, чтобы характеризовать тепловой эффект тока в различных точках проводника, выделим в нём элементарный участок трубки тока (рис. 6.8.). Запишем для этого элемента закон Джоуля-Ленца:
Здесь мы использовали хорошо известные соотношения:
—сопротивление участка цепи;
i = E — закон Ома в дифференциальной форме; dV = dl dS — объём выделенного элемента трубки тока.
Рис. 6.8.
Разделив количество выделившейся теплоты dQ на время dt, получим
тепловую мощность электрического тока:
Вт Джс
Отнеся эту величину к объёму элемента трубки тока, придём к удельной тепловой мощности:
|
(6.16) |
Формула (6.16) называется законом Джоуля – Ленца в дифференциальной форме.
Учитывая, что i = E = , это выражение можно записать в виде: