«Постоянный электрический ток»

1.Электрический ток. Характеристики электрического тока

2.Действия электрического тока

3.Законы Ома для участка цепи

3.1.Закон Ома в интегральной форме

3.2.Закон Ома в дифференциальной форме

4.Пример расчёта силы тока в проводящей среде

5.Закон Джоуля-Ленца в дифференциальной и интегральной формах

1. Электрический ток. Характеристики электрического тока

Электрическим током называется упорядоченное движение заряженных частиц, при котором происходит перенос электрического заряда.

В металлическом проводнике такими частицами являются свободные электроны. Они находятся в постоянном тепловом движении. Это движение происходит с высокой средней скоростью, но в силу его хаотичности не сопровождается переносом заряда. Выделим мысленно в проводнике элемент поверхности dS. За любой промежуток времени число электронов преодолевших эту поверхность слева направо в среднем будет равно числу частиц прошедших через эту поверхность в обратном направлении. Поэтому заряд, перенесённый через эту поверхность, окажется равным нулю.

Ситуация изменится, если в проводнике появится электрическое поле. Теперь носители заряда будут участвовать не только в хаотическом тепловом, но и в упорядоченном, направленном движении. Положительно заряженные носители будут двигаться по направлению поля, а отрицательные — в противоположном направлении.

В общем случае в переносе заряда могут принимать участие носители обоих знаков (например, положительные и отрицательные ионы в электролите). Скорость их движения будет складываться из скорости теплового и направленного движений. Хаотичность теплового движения приводит к тому, что среднее значение вектора скорости этого движения равно нулю, поэтому среднее значение результирующей скорости частиц будет равно средней скорости направленного движения.

Основной количественной характеристикой электрического тока является

сила тока.

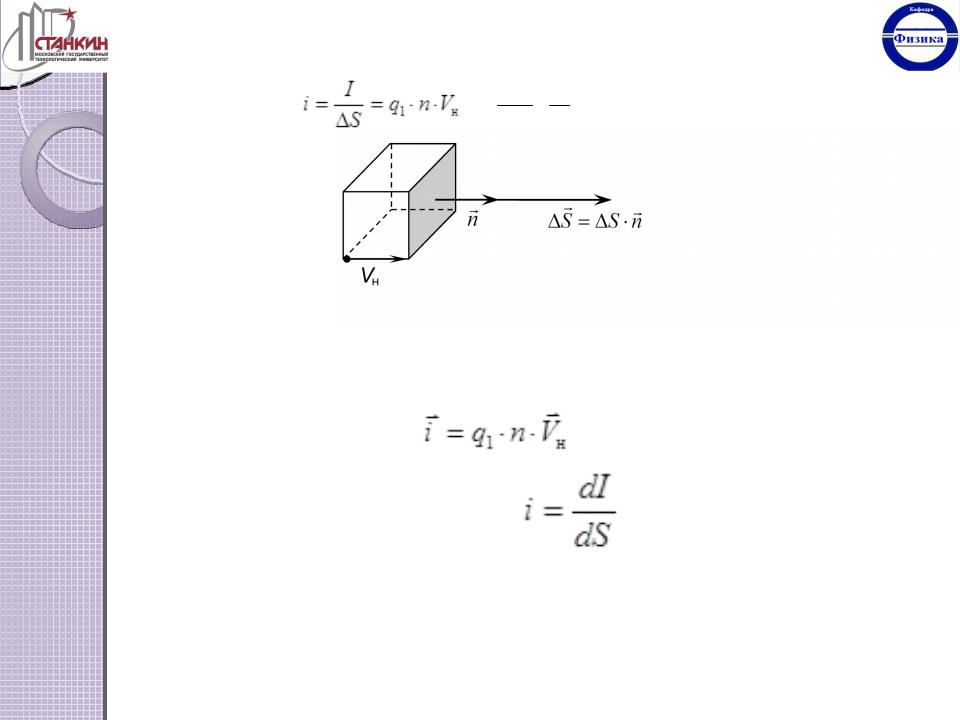
заряд, который протекает за единицу времени через единичную площадку, то есть плотность тока:

Рис. 6.1.

Поскольку скорость направленного движения заряженных частиц — векторная величина, это выражение записывают в векторном виде:

(6.3)

Модуль вектора плотности тока равен

(6.4)

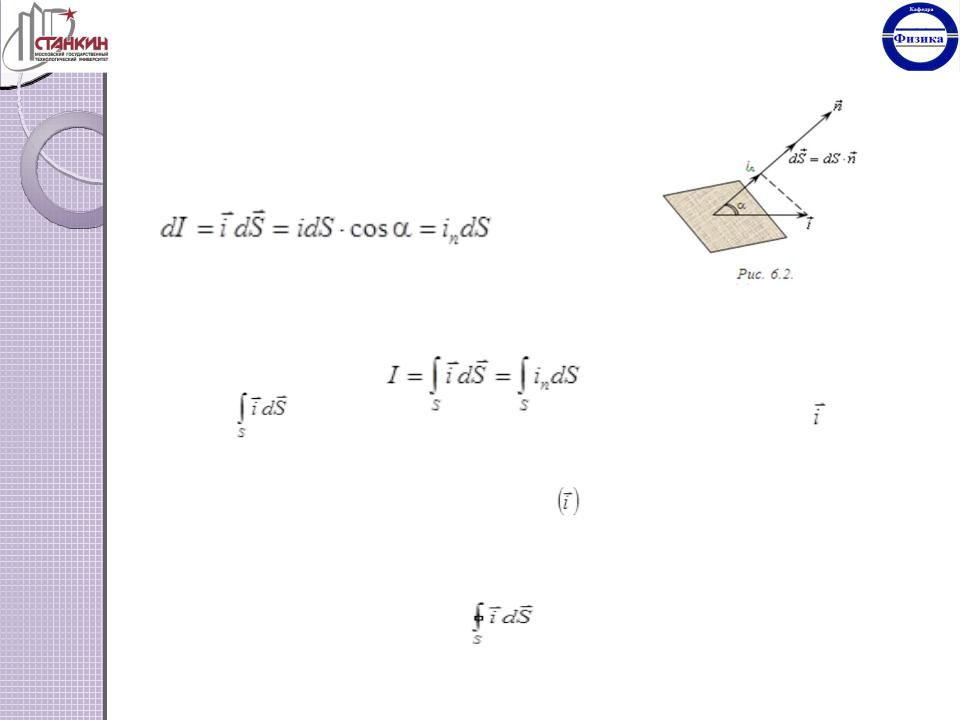
а направление совпадает с направлением скорости движения частиц , то естьили направлением напряжённости электрического поля в данной точке. Силу

тока, протекающего через элементарную площадку dS теперь можно записать в виде скалярного произведения двух векторов (рис. 6.2.):

Для того, чтобы вычислить силу тока через макроскопическое сечение S, нужно просуммировать все токи, протекающие через элементы этого сечения, то есть взять интеграл:

две основные характеристики электрического тока связаны между собой: сила тока равна потоку вектора плотности тока.

Продолжим разговор о потоке вектора Для этого в проводящей среде выделим замкнутую поверхность S (рис. 6.3.). Если известен вектор плотности тока в каждой точке этой поверхности, то легко вычислить заряд, покидающий объём, ограниченный этой поверхностью, в единицу времени:

Пусть внутри поверхности S находится заряд q, тогда за единицу времени он уменьшится на величину

Изменение заряда связано с его истечением из объёма, то есть: (6.7)

Это уравнение называется уравнением непрерывности. Оно представляет собой математическую запись закона сохранения электрического заряда.

3. Законы Ома для участка цепи

3.1. Закон Ома в интегральной форме

U, называется электрической проводимостью. Величина, обратная

проводимости называется электрическим сопротивлением проводника

Сопротивление зависит от материала проводника, его формы, размеров и состояния. Например, сопротивление цилиндрического проводника (проволоки):

R Sl

Здесь: — удельное сопротивление вещества, из которого сделан проводник, l и S — длина и площадь поперечного сечения проводника.

Сопротивление измеряется в омах. 1 Ом — это сопротивление такого проводника, в котором течёт ток I = 1 А при напряжении U = 1 В:

Удельное сопротивление в системе СИ измеряется в Ом   м:

.

Удельное сопротивление вещества зависит от температуры. В не слишком

широком диапазоне температур удельное сопротивление многих проводников является линейной функцией температуры:

Здесь: 0 — удельное электрическое сопротивление вещества при 0 С;— температурный коэффициент сопротивления.

Для всех чистых металлов = 0.037, то есть температурный

коэффициент их удельного сопротивления близок к температурному коэффициенту расширения идеальных газов. Температурный коэффициент сопротивления проводников 1 рода (металлов) I > 0, а II рода (электролитов)II < 0. Это означает, что с понижением температуры удельное сопротивление

металлов уменьшается, а электролитов — растёт.

При температурах близких к абсолютному нулю (0.2 20 К) сопротивление

многих металлов и их сплавов скачком уменьшается до нуля. Это состояние вещества называется сверхпроводящим. Впервые явление сверхпроводимости было обнаружено для ртути в 1911 году голландским физиком Камерлинг- Оннесом.

Рассмотренный закон пропорциональности тока в проводнике и напряжения: (6.11)

называется законом Ома в интегральной форме.

3.2. Закон Ома в дифференциальной форме

Представим себе электрический ток не в привычном для нас проводнике, а в однородной изотропной проводящей среде. При направленном

движении носители заряда перемещаются по траекториям, которые называются линии тока. Выделим в среде небольшую поверхность S. Линии тока, коснувшиеся границы

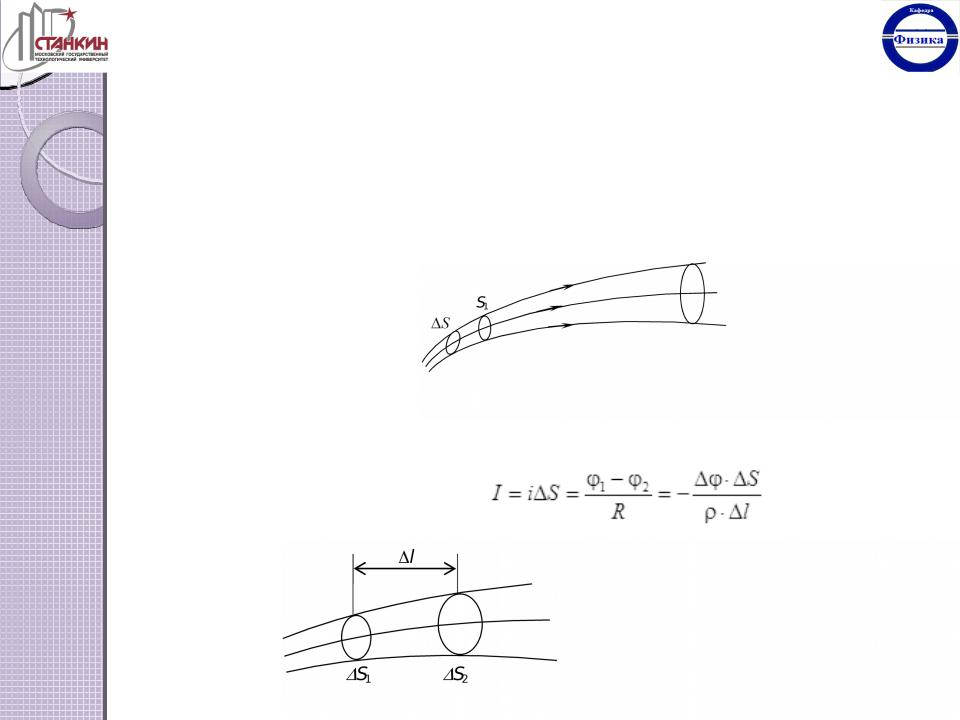
этой поверхности, в дальнейшем вырезают в пространстве трубку тока (рис. 6.4.). Особенность этой трубки состоит в том, что заряженные частицы, движущиеся внутри трубки тока, не пересекают её боковую поверхность, то есть они никогда не покидают свою трубку тока.

Рис. 6.4.

Выделим в трубке тока два эквипотенциальных сечения S1 и S2, отстоящие друг от друга на расстоянии l (рис. 6.5.). Потенциалы этих сечений 1 и

2 = 1 + . Для выделенного элемента трубки тока запишем закон Ома.

Рис. 6.5.

Сократив на S и введя удельную электропроводимость = , получим:

Этот результат становится точным, если перейти к пределу, устремив l к нулю. ТогдаS = S1 = S2, так как трубка становится цилиндрической. Кроме того:

Учитывая этот результат, плотность тока запишем как i = E,

или в векторном виде:

Это уравнение называется законом Ома в дифференциальной форме. В этом закон связываются две «локальные» характеристики тока: плотность тока в произвольной точке пространства и напряжённость электрического поля в той же точке.