
Синтез кулачковых механизмов.лист 3
.pdfотрезки +t от начала системы координат по направлению оси абсцисс (t) [3]:
+t1 =+t2 =+t3 = ... =+tn =+t.
Данные отрезки соответствуют шагу дифференцирования функции (шагу
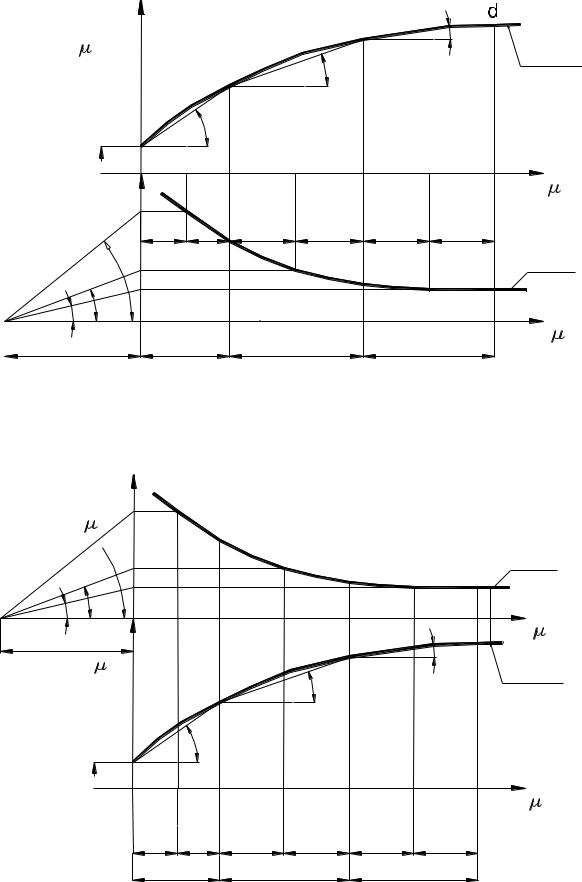
интегрирования). Из концов каждого отрезка +t проводят прямые, параллельные оси ординат S до пересечения с графиком функции перемещения. На кривой отмечают
точки a, b, c, d... Указанные точки соединяются отрезками прямых - хордами ab, bc, cd,.... В результате кривая S = f (t) заменяется ломаной линией abcd...
Система координат V, t строится под системой координат S, t так, чтобы их оси
S и V лежали на одной прямой линии (рис. 5.1). В системе координат V, t слева от точки OV откладывают произвольный отрезок POV, называемый полюсным расстоянием (постоянной дифференцирования или интегрирования). Из точки Р
(полюса) до пересечения с осью V проводят луч РВ под углом α , равным углу
наклона хорды ab к оси абсцисс, т. е. луч РВ должен быть параллелен хорде ab. Через точку В проводят горизонталь ВС до пересечения с ординатой середины отрезка +t . Точка С принадлежит искомой функции V = f '(t) = dS / dt . Повторяя по-
добные графические построения для каждого из участков ломаной линии abcd...,
получим для кривой V = f '(t) столько точек, сколько участков +t отложено по оси
абсцисс в системе координат S, t. Найденные точки соединяются плавной кривой линией.
При интегрировании функций графические построения выполняются в обратной последовательности. Строят системы координат S, t, V, t и график функции V = f '(t) . На оси абсцисс в системе координат S, t откладывают равные отрезки +t
(рис. 5.2). Из концов этих отрезков вверх проводятся ординаты до пересечения с
графиком функции V = f '(t) . Каждый полученный интервал делят пополам и
отмечают средние точки С, Е, G, Н,... на кривой V = f '(t) . Из этих точек проводят
горизонтали до пересечения с осью V. В системе координат V, t слева от точки OV на оси абсцисс откладывают произвольный отрезок POV. Точки В, D, F пересечения го-
ризонталей с осью ординат V соединяют с точкой Р (проводят семейство лучей для
средних точек отрезков +t ). По оси S в системе координат S, t откладывают начальное перемещение (для большинства решаемых задач S0 = 0). Из точки a
( yS = S0 ) на первом участке +t1 проводят хорду ab, параллельную лучу РВ,
проведенному из точки Р.
На втором участке из точки b проводят хорду bс, параллельную лучу PD.
Построения повторяют для всех участков +t . Полученная ломаная линия abсd...
заменяется плавной кривой линией функции S = f (t) .
S
S=
a
S0
V
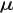 V=
V=
 α
α
θ β
hV
|
|
|
c |
θ |
S=f (t) |
|
|
β |
|
||
b |
|
|
|
||
|
|
|
|
||
|
|
|
|
|
|
α |
|
|
|
|
|
OS |
|
|
|
|
t |
C |
|
|
|
|
t = ... |
|
|
|
|
|
|
∆t/2 ∆t/2 |
∆t/2 |
∆t/2 |
∆t/2 |
∆t/2 |
|
D |
|
E |
|
|
V=f '(t) |
F |
|
G |
|
t |
|
OV |
|
|
|
||
∆t |
|
∆t |
∆t |
|
t = ... |
|
|
|
Рис. 5.1
V
V=
 α
α
θ β
hV S
S=
a
S0
C |
|
|
|
|
D |
E |
|
H |
V=f '(t) |
F |
|
G |
t |
|
OV |
|
|
||
|
|
c |
d |
t = ... |
|
|
θ |
S=f (t) |
|
|
β |
|
||
b |
|
|
||
|
|
|
||
|
|
|
|
|
α |
|
|
|
|
OS |
|
|
|
t |
|
|
|
|
t = ... |
∆t/2 ∆t/2 ∆t/2 |
∆t/2 |
∆t/2 |
∆t/2 |
|
∆t |
∆t |
|
∆t |
|
Рис. 5.2
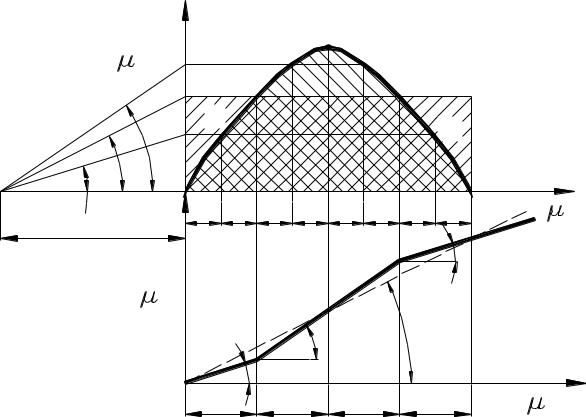
Ординаты yS интегральной функции S = f (t) полюсному расстоянию hV= POV. В связи с этим, выбирать так, чтобы максимальная ордината ys max
прямо пропорциональны POV полюсное расстояние следует функции S = f (t) получилась в
поле чертежа. Для этого откладывают максимальную ординату ys max (точка G) в
системе координат S, t (рис. 5.3). Затем проводят диагональ GOS. Площадь,
ограниченная кривой V = f '(t) заменяется равновеликим прямоугольником OVBCD.
Из точки В проводят луч РВ, параллельный диагонали GOS. Пересечение луча РВ с осью абсцисс t определяет положение полюса Р, тем самым, полюсное расстояние hV. Это построение базируется на следующей интегральной зависимости [4]:
D
yS max = ∫ yV dt = пл.OV EC ' HH 'C '' D = пл.OV BCD .
OV
При графическом интегрировании функции все точки (точки К и F на рис. 5.3) пересечение горизонталей (FE и КН) с осью V в системе координат V, t соединяют с
полюсом. В системе координат S, t на соответствующих им участках проводят хорды кривой S = f(t), параллельные лучам РК и PF.
Графики функций S = f (t) и V = f '(t) строят в заданных системах координат
при определенных значениях масштабных коэффициентов: S , V , t , соотношения между которыми находят из следующих зависимостей.
V
|
V= |
K |
|
H |
H' |
|
|
|
|
|
B |
C' |
|
C'' |
|
|
|||
|
|
|
|
C |
|
||||
|
|
F E |
|
|
|
|
|
||
|
|
|
|
|
E' |
|
|
||
P |
α |
α2 |
|
|
|
|
|
D |
t |
|
OV |
|
|
|
|
|
|
||
α1 |
|
|
∆t/2 |
∆t/2 |
∆t/2 ∆t/2 |
∆t/2 ∆t/2 |
∆t/2 ∆t/2 |
|
t = ... |
hV |
|
|
|
|
|
|
d |
G |
|
|
|
S |
|
|
|
|
|
||
|
|
|
|
|
|
α2 |
|
||
|
|
S= |
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
α2 |
α |
|
|
|
|
|
|
|
|
|
t |
|
||
|
|
OS |
|
α1 |
b |
|
|
|
|
|
|
∆t |
∆t |
∆t |
|
t = ... |
|||
|
|
|
|
∆t |
|
||||
|
|
|
|
|
Рис. 5.3 |
|
|
|
|
В общем виде скорость V является первой производной функции: |
|
||||||||
Vi = dSi |
/ dt, |
|
|
|
|
|
|
(5.1) |
|
где Si - текущее перемещение, которое связано с отрезком, изображающим это перемещение на чертеже, выражением:
Si = µS |
yS i , |
(5.2) |
|||||
где yS i - отрезок на чертеже, изображающий данное перемещение, мм; |
|||||||
S - масштабный коэффициент перемещения (4.12), |
м мм−1 ; |
||||||
t - время перемещения. Его величина на чертеже определяется по формуле: |
|||||||
t = µt Xt , |
(5.3) |
||||||
где Xt - отрезок на чертеже, изображающий время перемещения; |
|||||||
t |
- масштабный коэффициент времени, с мм−1. |
|
|||||
С учетом формул (5.2) и (5.3) выражение (5.1) примет вид |
|
||||||
V = |
|
µS |
dyS i |
, |
(5.4) |
||
|
|
|
|
||||
i |
|
|
µt |
dxi |
|
||
|
|
|
|
||||
где dyS i / dxi = tgα . |
|
||||||
Из прямоугольного треугольника POVB (рис. 5.1) получим: |
|
||||||
tgα = yV |
/ hV . |
|
|
|
|
||
1 |
|
|
|
|
|
|
|
Следовательно, в общем виде можно записать, что |
|
||||||
V = |
µS yV i |
, |
(5.5) |
||||
|
|||||||
i |
|
|
µt |
hV |
|
||
|
|
|
|
||||
Но можно также записать, что |
|
||||||
Vi |
= µV |
yV . |
(5.6) |
||||
|
|
|
|
i |
|
||
Приравняв выражения (5.5) и (5.6), найдем зависимость для определения масштабного коэффициента скорости:
µV |
= |
S |
= ...м/ с мм. |
(5.7) |
|
|
|
||||
|
|
µt hV |
|
||
Аналогичным образом находят выражение для определения масштабного |
|||||
коэффициента ускорения µa , если в этом появится необходимость: |
|||||
µa = |
V |
|
= ...м/ с2 мм, |
(5.8) |
|
|
|||||
|
|
µt ha |
|
||
где ha |
- |
полюсное расстояние в системе координат α , t |
при графическом |
||
интегрировании, мм;
α - ускорение перемещения - вторая производная функции S = f (t) , м/ с2 : a = d 2S / dt2 = f ′′(t).
5.2. Указания на построение графиков закона перемещения толкателя
При отсутствии данных автоматизированного расчета параметров αϕ , Vϕ , S
кулачкового механизма студент строит графики [V ,ϕ ] и [S,ϕ ] графическим
интегрированием закона ускорения α = f (t) перемещения толкателя, заданного в
описании проектируемого станка. Сначала на левой части чертежного листа
наносится сетка с указанием осей α , ϕ ; V ,ϕ и S,ϕ при соблюдении всех рекомендаций по выбору отрезков абсцисс и максимальных ординат, указанных в разделе 4. Затем в системе координат α ,ϕ на угле ϕуд поворота кулачка следует
построить график [α ,ϕ ] функции ускорения перемещения толкателя (рис. 5.4).
Полюсное расстояние hα = π O , необходимое для построения графика [V ,ϕ ]
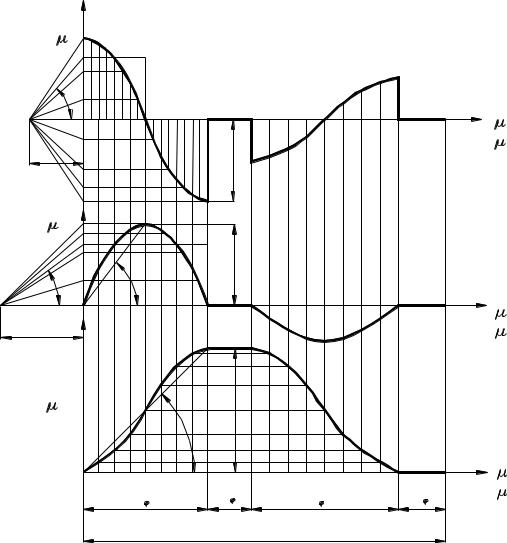
скорости толкателя графическим интегрированием графика |
[α ,ϕ ] |
ускорения, |
||||
находят следующим образом. Из начала О системы координат |
V ,ϕ |
проводят |
||||
прямую OF под углом α |
к оси абсцисс, соединяющую |
О |
с |
вершиной |
F |
|
максимальной ординаты |
графика скорости. Площадь |
ORM, |
ограниченная |
|||
графиком ускорения, заменяют равновеликим прямоугольником OQLM. Из вершины |
||||||
Q этого прямоугольника к оси абсцисс под углом α проводят прямую линию Qπ |
до |
|||||
пересечения с осью абсцисс, т. е. параллельную прямой OF |
на графике [V ,ϕ ]. |
|||||
Определив полюсное расстояние hα , графическим интегрированием графика [α ,ϕ ],
описанным в подразделе 5.1, находят ординаты графика [V ,ϕ ] скорости толкателя.
|
α |
R |
|
|
α= |
L |
|
|
|
Q |
|
|
α |
|
M |
|
π |
O |
|
|
|
|
|
|
hα |
|
|
|
V |
|
F |
|
V= |
|
|
|
C |
|
|
|
|
|
|
P |
β |
|
α |
|
|
|
|
|
hV |
O |
|
|
|
|
S
S=
α =max
D
V =max
H
A
β |
Smax= |
ϕ, t
ϕ = ...
t = ...
ϕ, t
ϕ = ...
t = ...
O 0 1 2 3 4 5 6 7 8 |
|
|
ϕ, t |
8 7 6 |
5 4 3 2 1 0 |
ϕ = ... |
|
X УД |
X ДС |
X ПР |
t = ... |
X БС |
|||
|
2π |
|
|
Рис. 5.4
Полюсное расстояние hV =PO в системе координат V ,ϕ , необходимое для
построения |
графика [ S,ϕ ] |
находится аналогично |
определению |
полюсного |
расстояния |
ha. В системе |
координат [ S,ϕ ] проводят |
луч ОА под |
углом β , |
соединяющий начало О координат с вершиной А максимальной ординаты графика
[ S,ϕ ]. Площадь |
OFH, ограниченная графиком |
[V ,ϕ ] на угле |
ϕуд , заменяют |
равновеликим прямоугольником OCDH, из вершины С которого проводят прямую СР |
|||
под углом β к |
оси абсцисс, т.е. параллельную |
прямой ОА на |
графике [ S,ϕ ]. |
Графическим интегрированием функции [V ,ϕ ], описанным в подразделе 5.1, строят график [ S,ϕ ] перемещения толкателя.
Ординаты графика [α ,ϕ ] на угле ϕпр приближения определяют из условия
равенства дифференциалов d2s на углах ϕуд и ϕпр [3]:
d 2 S = aуд (dtуд )2 и d 2S = aпр (dtпр)2 .
При равномерном вращении кулачка можно считать, что
dtуд / dtпр = tуд / tпр = ϕ уд /ϕпр;
Следовательно,
|
a |
уд |
|
ϕ |
пр |
|
2 |
|
|
|
|
= |
|
|
|
; |
(5.9) |
||
|
|
|
|
|
|||||
|
aпр |
|
ϕ |
|
|
|
|
|
|
|
|
уд |
|
|
|||||
или |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
ϕ |
уд |
|
|
||
|
ya |
= |
|
|
ya |
(5.10) |
|||
|
|
|
|||||||
|
|
пр |
|
|
|
|
|
|
уд |
|
|
|
ϕпр |
|
|||||
|
|
|
|
|
|||||
Аналогичным образом находят взаимосвязь ординат графика [V ,ϕ ] скорости
толкателя на углах ϕуд |
и ϕпр : |
|||||||
V |
= |
ϕ уд |
V |
|
|
(5.11) |
||
|
|
|
|
|||||
пр |
|
ϕпр |
уд |
|
|
|||
или |
|
|
ϕ уд |
|
|
|
|
|
y |
= |
y |
|
(5.12) |
||||
|
|
|||||||
V |
|
ϕпр |
V |
|
|
|||
пр |
|
|
уд |
|
||||
|
|
|
|
|
|
|
||
Ординаты yS перемещения толкателя на углах ϕуд и ϕпр принимают равными между
собой. При графическом построении допускается взаимное пересечение графиков. На осях координат следует указать численные значения масштабных
коэффициентов с указанием их размерностей: угла µϕ и времени µt поворота кулачка; перемещения µS , скорости µV и ускорения µa толкателя. Для определения
этих величин необходимо воспользоваться формулами (4.12),(5.7) и (5.8). Следует
так же указать максимальные значения скорости и ускорения толкателя (4.13; 4.14). На основе графиков [α ,ϕ ], [V ,ϕ ] и [S,ϕ ] в интервале фазовых углов ϕуд и ϕпр поворота кулачка нужно составить таблицу натуральных параметров αϕ , Vϕ , S . Они
необходимы для построения диаграммы аналогов скорости или ускорения по определению рациональных размеров проектируемого кулачкового механизма. При
расчёте текущих значений αϕ , Vϕ , S используют зависимости:
a |
= 1000 |
µa |
ya |
, |
(5.13) |
|||
|
i |
|
||||||
ωk2 |
||||||||
ϕ |
|
|
|
|
||||
V |
= 1000 |
µV yVi |
, |
(5.14) |
||||
|
||||||||
ϕ |
|
|
ωk |
|
|
|||
|
|
|
|
|
||||
Si |
= 1000 µS |
ySi , |
|
(5.15) |
||||
При вычислении значений αϕ , Vϕ , S по данным формулам единицей измерения является миллиметр (мм).
6. Определение рациональных размеров основных звеньев кулачкового механизма
6.1. Минимизация геометрических размеров звеньев кулачкового механизма
Задачу синтеза кулачкового механизма решают на основе учета его механических показателей и качественных критериев. Наиболее важными
механическими показателями работы кулачковых механизмов являются угол давления, коэффициент полезного действия механизма, коэффициент возрастания
усилия, коэффициент прочности звеньев, коэффициент динамичности, а качественными критериями - удельное давление и коэффициент износа элементов в высшей кинематической паре [1]. Большинство перечисленных показателей
взаимосвязаны и зависят в основном от угла давления. Учитывая значимость этого параметра для работы кулачкового механизма, при синтезе механизма ему
придается критериальное значение. Задаваясь ограничением по углу давления на ведомое звено, можно графически или аналитически определить минимальные размеры основных звеньев кулачкового механизма, при которых реализуется
заданный закон движения толкателя и требуемые условия работы при минимальной металлоемкости его конструкции.
Основными геометрическими размерами кулачковых механизмов являются
следующие величины:
ϕ уд, ϕдс, ϕпр и ϕбс - |
фазовые углы поворота кулачка, |
град (при проектировании |
|||||
задаются); |
|
|
|
|
|
|
|
S0 - |
максимальное перемещение толкателя, мм (при проектировании |
||||||
|
задается); |
|
|
|
|
|
|
I - |
длина толкателя, мм (при проектировании задаётся); е - |
||||||
|
эксцентриситет смещения оси перемещения толкателя |
||||||
|
относительно оси вращения кулачка (при проектировании |
||||||
e - |
задается), |
|
|
|
|
|
|
эксцентриситет смещения оси перемещения толкателя |
|||||||
|
относительно оси вращения кулачка (при проектировании |
||||||
|
задается); |
|
|
|
|
|
|
β - |
угол размаха колебаний толкателя, град (при проектировании |
||||||
υ * - |
задается); |
|
|
|
|
|
|
допустимый угол давления на толкатель, град (при |
|||||||
|
проектировании задается); |
|
|
|
|
||
R0 - |
начальный радиус центрового профиля кулачка, мм (при |
||||||
α - |
проектировании определяется по диаграмме аналогов скорости); |
||||||
межосевое расстояние (расстояние между осью вращения |
|||||||
|
кулачка и осью толкателя), мм (при проектировании определяется |
||||||
|
по диаграмме аналогов скорости); |
|
|
|
|
||
RM - |
начальный радиус конструктивного профиля кулачка, мм (при |
||||||
|
проектировании определяется по диаграмме аналогов ускорения); |
||||||
RС- |
средний |
радиус |
цилиндрического |
кулачка, |
мм |
(при |
|
|
проектировании вычисляется аналитически). |
|
|
||||
Возможное |
сочетание |
указанных параметров |
в |
кулачковом |
механизме |
||
определяется его типом. Для нахождения области минимально допустимых
значений того или иного размера профиля кулачка и возможного расположения его оси вращения рекомендуется строить диаграммы аналогов ускорения или скорости в зависимости от перемещения толкателя, которые позволяют проектировщику
выбрать рациональные размеры звеньев по заданному углу давления при соблюдении условий эксплуатации.
6.2. Определение основных размеров звеньев кулачкового механизма типа 1 а
Диаграмма [Vϕ , S] аналогов скорости для кулачкового механизма с роликовым
коромысловым толкателем (рис. 8.17, а) строится в полярной системе координат при
масштабном коэффициенте длин S , который определяется выражением (8.33):
S = 0.001 S0 / yS max |
= 0.001 Vϕ max / yVϕ max , |
(6.1) |
|
где S0 ,Vϕ max - максимальные величины, мм; |
|
||
yS max , yVϕ max |
- отрезки, изображающие соответственно величины S0 ,Vϕ max , мм. |
||
Координаты |
S,Vϕ |
для диаграммы [Vϕ S] |
следует взять из результатов |
автоматизированного расчета параметров механизма или вычислить их по формулам (5.14, 5.15):
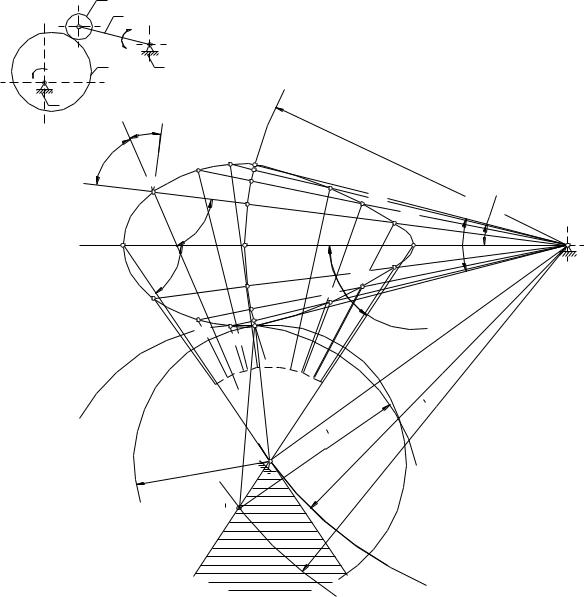
|
а) |
2 |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
O2 |
|
|
|
|
|
|
|
||
ωK |
|
1 |
4 |
|
|
|
|
|
|
б) |
||
|
|
O1 |
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
n |
υi |
|
|
|
|
|
|
|
|
|
|
|
γ |
|
|
|
|
|
B6уд B7уд |
A8 |
|||
|
|
|
B5уд |
|
|
|
|
|
|
|
A7 |
|
|
|
|
|
|
|
|
|
|
|
ϑ |
i |
A6 |
|
|
|
|
|
|
|
|
|
- |
A5 |
||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
0 |
° |
|
|
A4 |
|
|
B4уд |
|
|
|
* |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
- |
ϑ |
|
|
|
|
|
|
|
|
|
|
9 |
0 |
° |
|
|
|
|
|
|
A3 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
B3уд |
|
|
|
|
|
|
|
|
A2 |
|
|
|
|
|
|
|
|
|
B2уд B1уд |
A1 |
||
|
|
|
|
|
|
|
|
|
A0 |
|||
n
0 |
O1 |
R |
|
|
O1 |
S =... м/мм
B7пр |
l |
|
B6пр |
||
|
||
|
B5пр |
|
|
B4прβ |
|
|
B3пр |
B2пр
B1пр
90°-ϑ **
aw
a w
R0
2 / β
O2
|
|
|
Рис. 6.1 |
|
Из точки O2 (рис. 6.1, б) проводят дугу радиуса O2A0 , длина которого |
||||
соответственно равна: |
|
|||
O A = 0.001 |
l |
, |
(6.2) |
|
|
||||
2 |
0 |
S |
|
|
|
|
|
||
где l - длина толкателя, мм. |
|
|||
Длина дуги ограничивается центральным углом β |
с вершиной в точке O2 , |
|||
равным углу размаха толкателя. Отрезки текущих перемещений Si , толкателя в масштабе S откладывают на дуге от точки A0 в пределах заданного угла β . Для повышения точности графических построений рекомендуется разметку пути центра
A ролика выполнять малыми отрезками длин. Из центра O2 через полученные точки
A1,A2 ,A3 ,...,AN на дуге перемещения A0AN толкателя проводят лучи
O2A1,O2A2 ,O2A3 ,...,O2AN , на которых откладывают соответствующие аналоги
скорости толкателя в масштабе µS . Причем, отрезки аналогов скорости на угле ϕУД
удаления откладывают слева от дуги, являющейся траекторией центра ролика
коромыслового толкателя, а отрезки аналогов скорости на угле ϕ ПР приближения – справа, при вращении кулачка против часовой стрелки, а при его вращении в противоположную сторону – наоборот.
Точки Bi соединяют плавной кривой, которая является диаграммой [Vϕ , S]
аналогов скорости перемещения толкателя. Скорость толкателя перпендикулярна
радиусу – лучу, проходящему через точку Bi , т.е. диаграмма [Vϕ , S] является
геометрическим местом точек аналогов скорости, повернутых на 900 .
Следовательно, на диаграмме [Vϕ , S] угол γ , образованный пересечением луча O2 Bi
и нормали n − n , равен:
γ = 900 − ϑ . |
(6.3) |
i |
|
В связи с этим, для определения начального радиуса R0 |
центрового профиля |
кулачка и положения его оси O1 вращения, необходимо из точек, соответствующих максимальным аналогам скорости на углах ϕУД и ϕ ПР , провести прямые под углами
900 − ϑ и 900 − ϑ к этому лучу. Угол ϑ есть предельный угол давления на угле ϕ ПР
приближения. При силовом замыкании высшей кинематической пары кулачкового механизма он берется на (30...50)% больше, чем угол ϑ , т.к. в этом случае
толкатель является ведущим звеном механизма, |
и угол давления не играет роли. |
При замыкании необходимо принять: |
|
ϑ = ϑ |
(6.4) |
Заштрихованная зона на рис 6.1,б является областью допустимых положений
оси вращения кулачка, а огибающие прямые этой зоны – ее предельными положениями. Отрезок O1A0 соответствует начальному радиусу R0 центрового
профиля кулачка, а отрезок O1O2 - межосевому расстоянию aw центров вращения
кулачка и толкателя при масштабном коэффициенте. Действительные размеры этих величин будут:
R = 103 |
µ |
S |
O A , |
(6.5) |
0 |
|
1 0 |
|
