
2013 - Конспект, 8лекций
.pdf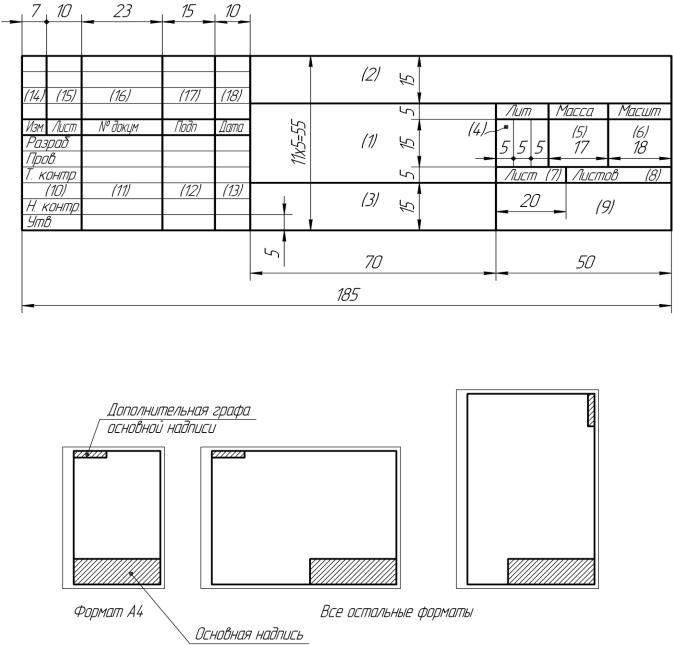
Основная надпись (по ГОСТ 2.104-68)
– регламентированная ГОСТ таблица (Рис 3-3), располагаемая в правом нижнем углу конструкторского документа;
Рис 3-3
на листах формата А4 основную надпись располагают только на короткой стороне (Рис 3-4)
Рис 3-4
Линии (по ГОСТ 2.303-68)
В качестве исходной принята сплошная толстая основная линия, толщина которой выбирается в интервале 0,5…1,4 мм. Толщины остальных линий зависят от выбранной толщины основной линии (табл. 1). В СТАНКИНе принято s=0,8…1,0 мм.
21

Таблица 1
Изображения предметов на технических чертежах есть совокупность проекций точек, принадлежащих предметам. При этом считают, что предмет располагается между наблюдателем и соответствующей плоскостью проекций (ГОСТ 2.305–68).
22

Изображение многогранников.
Многогранник
-геометрическое тело, ограниченное со всех сторон плоскими фигурами – многоугольниками, называемыми гранями. Линии пересечения граней между собой называются рёбрами, точки пересечения ребер между собой называются вершинами.
Пирамида
-многогранник, у которого одна грань (основание) представляет собой многоугольник, а остальные грани – треугольники с общей вершиной или трапеции (усечённая пирамида).
Построение проекции многогранника на плоскости проекций сводится к построению проек-
ций точек (вершин). Например, проецируя пирамиду SABC на плоскость проекций 2 (Рис. 3- 6), строят проекции вершин S , A , B , C, и, как следствие, рёбер S A , S B , S C , A C , A B , B C, основания A B C и граней S A B , S A C , S B C. На чертеже пирамида задаётся проекциями её основания и вершины (Рис. 3-5).
Рис 3-5 Рис 3-6 Если на чертеже на поверхности многогранника задана одна проекция точки и требуется
найти другую её проекцию, то можно провести через заданную точку прямую, принадлежащую поверхности многогранника, найти проекции прямой, а проекции точки должны находиться на одноимённых проекциях прямой (Рис. 3-6).
Призма - многогранник, две грани которого (основания) являются равными многоугольниками с вза-
имно параллельными сторонами, а все другие грани – параллелограммы. Признаки изображения на чертеже призмы: 1) наличие на чертеже только прямолинейных отрезков (проекции рёбер); 2) наличие параллелограммов или прямоугольников (проекции боковых граней); 3) наличие одного или двух любых многоугольников (проекции оснований) – рис. 3-7.
23

Рис 3-7
Согласно ГОСТ 2.305-68: "Вид
–изображение обращённой к наблюдателю видимой части поверхности предмета. Для уменьшения количества изображений допускается на видах показывать необходимые невидимые части поверхности предмета при помощи штриховых линий".
"Разрез
–изображение предмета, мысленно рассечённого одной или несколькими плоскостями. На разрезе показывается то, что получается в секущей плоскости и что расположено за ней".
"Сечение
–изображение фигуры, получающейся при мысленном рассечении предмета одной или несколькими плоскостями. На сечении показывается только то, что получается непосредственно в секущей плоскости".
Построение проекций контуров и натурального вида сечений многогранников.
Вкачестве секущих плоскостей используются проецирующие плоскости (т.е. плоскости перпендикулярные хотя бы одной плоскости проекций). Контуром сечения является множество точек, одновременно принадлежащих секущей плоскости и поверхности предмета. Контур сечения многогранника плоскостью представляет собой плоский многоугольник (отсек плоскости), число сторон которого равно числу пересекаемых граней. Стороны такого многоугольника есть линии пересечения граней и секущей плоскости, а его вершинами являются точки пересечения рёбер с секущей плоскостью (Рис. 3-8).
При необходимости определения проекций точек пересечения прямой с многогранником можно провести через прямую плоскость – посредник, найти проекцию контура пересечения плоскости с многогранником, затем найти проекции точки пересечения прямой с проекцией контура (Рис. 3-8).
Для того чтобы получить натуральный вид сечения, можно преобразовать чертёж спосо-
бом замены плоскостей проекций, использовав дополнительную плоскость проекций ( 4) па-
раллельную секущей плоскости ([4//)и перпендикулярную одной из основных плоскостей проекций (например 2, 2), и на неё спроецировать сечение: 1) [ 4// , 2] 4 2; 2) 123 4, 1 2 3 = | 123| (Рис. 3-8).
24
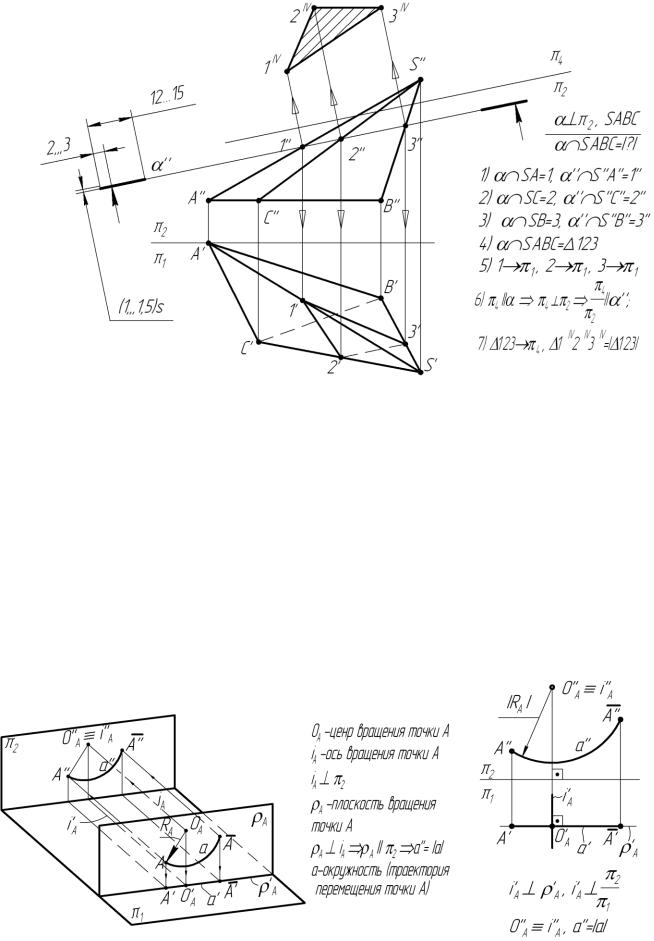
Рис 3-8
[1] §§ 39 – 42
ЛЕКЦИЯ 4
Способы преобразования чертежа вращением. Поворот заданных плоских фигур вокруг проецирующих прямых и линий уровня.
При вращении вокруг некоторой неподвижной прямой (оси вращения - i) каждая точка вращаемой фигуры перемещается в плоскости, перпендикулярной к оси вращения (в плоскости вращения - , i). Точка перемещается по окружности, центр которой находится в точке пересечения оси с плоскостью вращения (центр вращения – O, i=О), а радиус окружности (радиус вращения - R) равен расстоянию от вращаемой точки до центра (рис. 4-1).
СПОСОБ ВРАЩЕНИЯ ВОКРУГ ОСЕЙ, ПЕРПЕНДИКУЛЯРНЫХ К ПЛОСКОСТЯМ ПРОЕКЦИЙ (вокруг проецирующих прямых)
Вращение точки На плоскость проекций, к которой ось вращения перпендикулярна, окружность, по которой пе-
ремещается точка, проецируется без искажения (рис. 4-1, 4-2).
Рис 4-1 |
Рис 4-2 |
25

Вращение прямой сводится к вращению двух точек этой прямой (рис. 4-3), каждая из которых поворачивается на
одинаковый угол . Поворотом вокруг проецирующей прямой прямую линию общего положения можно привести к частному положению, сделав её параллельной плоскости проекций (рис.
4-4).
Рис 4-3 Рис 4-4 Двумя поворотами вокруг проецирующих прямых прямую линию общего положения
можно привести к частному положению, сделав её перпендикулярной плоскости проекций (рис.
4-4).
Вращение плоскости сводится к повороту принадлежащих ей точек и линий (рис. 4-5). Двумя поворотами плоской
фигуры вокруг проецирующих прямых можно расположить её (фигуру) параллельно относительно плоскости проекций, в результате чего проекция фигуры на упомянутую плоскость проекций будет иметь натуральный вид (рис.4-5).
Рис 4-5
26

В результате первого поворота фигуру делают перпендикулярной одной из плоскостей проекций (например, 2), после второго поворота фигуру располагают параллельно другой плоскости проекций (например, 1). При этом используют линии уровня, принадлежащие фигуре (горизонталь фронталь или профильную прямую), одну из которых при первом повороте делают проецирующей.
Натуральный вид контура сечения какого либо тела проецирующей плоскостью можно определить способом поворота вокруг проецирующей линии (рис. 4-6).
Рис 4-6
[1] §§ 34, 35, 37
СПОСОБ ВРАЩЕНИЯ ВОКРУГ ОСЕЙ, ПАРАЛЛЕЛЬНЫХ ПЛОСКОСТЯМ ПРОЕКЦИЙ (линий уровня – горизонтали h, фронтали f, профильной прямой p).
Поворот осуществляют так, чтобы поворачиваемая плоскость стала параллельной одной из плоскости проекций 1, 2 или 3.
Вращение точки.
Точка А вращается вокруг центра вращения ОА в плоскости вращения А, которая перпендикулярна оси вращения h (Аh). После поворота отрезок ОАА, равный радиусу вращения точки А (RA) стал параллелен плоскости проекций 1 (рис. 4-7) и, следовательно, его проекция на эту плоскость стала равна натуральной величине радиуса вращения (после поворота OAA = |RA|).
Рис 4-7
27

При этом натуральную величину радиуса вращения точки |OAA| = RA определяют способом прямоугольного треугольника (рис. 4-8, 4-9) или с помощью дополнительной плоскости проекций (преобразования чертежа способом замены плоскости проекций; см. лекцию 1).
Рис 4-8
Рис 4-9
Вращение плоскости (например ) сводится к повороту одной принадлежащей ей точки А; две другие точки С и 1,
определяющие положение плоскости, можно взять на линии уровня плоскости (горизонтали h , фронтали f или профильной прямой p ), вокруг которой поворачивают плоскость (рис. 4-10).
28

Рис 4-10
При этом удобно использовать описанный выше способ прямоугольного треугольника для определения натуральной величины радиуса вращения точки А (рис. 4-8, 4-9).
[1] §§ 34, 35, 37
ЛЕКЦИЯ 5
Изображения поверхностей вращения (цилиндра, конуса, сферы) с нанесением размеров. Точки на поверхностях. Построение проекций контуров и натурального вида сечений (наклонных) цилиндра,
конуса, сферы проецирующими плоскостями.
Изображения поверхностей вращения (цилиндра, конуса, сферы). Точки на поверхностях.
Прямые круговые цилиндр и конус
задаются высотой h и диаметром основания d (Рис. 5-1 и 5-2, соответственно).
Рис 5-1
29

Рис 5-2
Сфера
задаётся диаметром d. (Рис. 5-3).
Рис 5-3
Поверхность вращения есть след образующей линии при вращении её вокруг неподвижной прямой, называемой осью вращения.
30
