
- •Перспективные изображения
- •11.Видовое преобразование как аппарат построения аксонометрических изображений. Видовое преобразование
- •12.Перспективное преобразование и её проективная концепции. Перспективное преобразование
- •13.Внутреннее компьютерное представления каркаса геометрической модели.
- •14.Основные принципы построения алгоритмов генерации простых геометрических объектов. Генерация файла для геометрического объекта «тор». Генерация файла для геометрического объекта «тор»
- •26.Определение нормали к поверхности. Определение нормали к поверхности
- •21.Интерполяция точечного каркаса функции полиномами. Интерполяция полиномами
- •23.Построение в-сплайна.
23.Построение в-сплайна.
Рассмотрим ещё
один способ построения гладких кривых
по форме В-сплайна.
Будем использовать параметрическое
представление кривых. Любая точка части
кривой между двумя заданными
последовательными точками
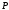 и
и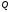 будет иметь координаты
будет иметь координаты и
и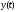 ,
где
,
где увеличивается от
увеличивается от до
до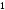 ,
если отслеживается часть кривой от
точки
,
если отслеживается часть кривой от
точки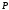 до
точки
до
точки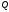 .
Можно считать, что
.
Можно считать, что - это время.
- это время.
Если имеются заданные точки

то часть кривой
В-сплайна
между двумя последовательными точками
 и
и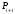 получается путем вычисления функций
получается путем вычисления функций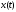 и
и для изменения
для изменения от
от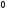 до
до

Эти уравнения содержат следующие коэффициенты:
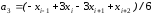
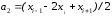
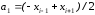
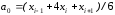
а коэффициенты
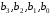 вычисляются по значениям
вычисляются по значениям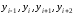 аналогичным образом. Вышеприведенные
формулы пригодны для эффективных
вычислений. Вычисление значений
аналогичным образом. Вышеприведенные
формулы пригодны для эффективных
вычислений. Вычисление значений производится быстрее по правилу Горнера,
чем по обычному полиномиальному
выражению. Коэффициенты
производится быстрее по правилу Горнера,
чем по обычному полиномиальному
выражению. Коэффициенты вычисляются только однажды для каждого
сегмента кривой, что очень важно,
поскольку на каждом сегменте кривой
может вычисляться большое число
промежуточных точек
вычисляются только однажды для каждого
сегмента кривой, что очень важно,
поскольку на каждом сегменте кривой
может вычисляться большое число
промежуточных точек и
и .
.
Для получения
некоторого представления о свойствах
кривой в точках стыковки двух сегментов
рассмотрим функцию
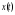 и ее первую и вторую производные для
значений
и ее первую и вторую производные для
значений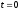 и
и (функция
(функция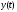 будет обладать аналогичными свойствами)
будет обладать аналогичными свойствами)
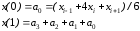
Используя уравнение коэффициентов, после упрощения получаем

Можно видеть, что
значение
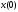 не равно в точности
не равно в точности -координате
-координате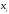 точки
точки :
оно зависит от позиций точек
:
оно зависит от позиций точек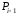 и
и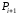 .
Из рисунка 5.1.7 видно, что точка
.
Из рисунка 5.1.7 видно, что точка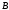 является точкой сегмента
является точкой сегмента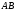 ,
но одновременно и начальной точкой
сегмента
,
но одновременно и начальной точкой
сегмента .
.
Для первого сегмента имеем
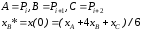

Рис.5.1.7. Три последовательные точки
где через
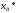 обозначено вычисленное значение
координаты
обозначено вычисленное значение
координаты для точки
для точки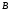 .
Рассматривая эту же точку как принадлежащую
сегменту
.
Рассматривая эту же точку как принадлежащую
сегменту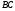 ,
получим
,
получим

Отсюда видно, что
оба способа вычисления значения
 дают одинаковый результат, что означает
непрерывность функции
дают одинаковый результат, что означает
непрерывность функции в точке
в точке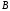 .
Продифференцировав
.
Продифференцировав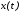 дважды, найдем производные
дважды, найдем производные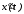 и
и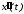 .
Подставляя в них значения
.
Подставляя в них значения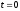 и
и ,
как это было сделано для
,
как это было сделано для ,
можно будет убедиться, что производные
непрерывны в точке
,
можно будет убедиться, что производные
непрерывны в точке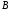 .
Поскольку функция
.
Поскольку функция и ее первые
и ее первые
две производные тоже непрерывны, то становится ясно, что кривая В-сплайна очень гладкая.
Для расчета любого
сегмента кривой между точками
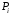 .
и
.
и используются также точки
используются также точки и
и .
Из этого следует, что первый сегмент
кривой будет располагаться между точками
.
Из этого следует, что первый сегмент
кривой будет располагаться между точками и
и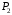 ,
а последний — между точками
,
а последний — между точками и
и .
Так что начальная и конечная точки всей
кривой будут располагаться вблизи
.
Так что начальная и конечная точки всей
кривой будут располагаться вблизи и
и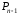 но не вблизи
но не вблизи и
и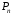 .
Приведенная ниже программа считывает
числа
.
Приведенная ниже программа считывает
числа
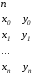
из файла CURV.DAT. При
выводе каждая из
 точек обозначается маркером в виде
креста. Затем вычерчивается кривая В-
сплайна.
точек обозначается маркером в виде
креста. Затем вычерчивается кривая В-
сплайна.
/* CURVFIT: Сглаживание кривой с применением В-сплайна */
/* Curve fitting using В splines */
#include "stdio.h"
#define MAX 100
#define N 30
main()
{ float x[MAX], y[MAX], eps=0.04, X, Y, t, xA, xB, xC, xD,
yA, yB, yC, yD, a0, a1. a2, аЗ, bО, b1, b2, bЗ;
int n, i, j, first;
FILE *fp;
Fp=fopen(“curv.dat", "r");
if (fp==NULL) { printf /* "There is no file curv.dat" */
("Нет файла curv.dat\n”); exit(1); }
fscanf(fp, "%d", &n):
for(i=0;i<=n;i++)
if (fscanf(fp,"%f %f", x+i, y+i)<=0)
{ printf /* "Reading beyond the end of file curv.dat" */
("Считывание выходит за пределы файла curv.dat\n”); exit(1);
}
initgr();
/* Mark the given points: */
/* Заданные точки отмечаются маркером: */
for(i=0;i<=n;i++)
{X=x[i];Y=y[i];
move(X-eps, Y-eps); draw(X+eps, Y+eps);
move(X+eps, Y-eps); draw(X-eps, Y+eps);
}
first=-1;
for(i=1;i<n-1;i++)
{ xA=x[i-1]; xB=x{i]; xC=x[i+1]; xD=x[i+2];
yA=y[i-1]; yB=y[i]; yC=y[i+1]; yD=y[i+2];
a3=(-xA+3*(xB-xC)+xD)/6.0; b3=(-yA+3*(yB-yC)+yD)/6.0;
а2=(хА-2*хВ+хС)/2.0; b2=(уА-2*уВ+уС)/2.0;
a1=(xC-xA)/2.0; b1=(уС-уА)/2.0;
a0=(xA+4*xB+xC)/6.0; b0=(уА+4*уВ+уС)/6.0;
for(j=0;j<=N;j++)
{t=(float)j/(float)N;
X=((a3*t+a2)*t+a1)*t+a0;
Y=((b3*t+b2)*t+b1)*t+b0;
it (first) { first=0; move(X, Y);} else draw(X, Y);
}
}
endgr(); fclose(fp);
}
