
- •Перспективные изображения
- •11.Видовое преобразование как аппарат построения аксонометрических изображений. Видовое преобразование
- •12.Перспективное преобразование и её проективная концепции. Перспективное преобразование
- •13.Внутреннее компьютерное представления каркаса геометрической модели.
- •14.Основные принципы построения алгоритмов генерации простых геометрических объектов. Генерация файла для геометрического объекта «тор». Генерация файла для геометрического объекта «тор»
- •26.Определение нормали к поверхности. Определение нормали к поверхности
- •21.Интерполяция точечного каркаса функции полиномами. Интерполяция полиномами
- •23.Построение в-сплайна.
1. Основные этапы развития компьютерной графики. Основные направления развития компьютерной графики.
2. Приложения компьютерной графики. Виды представления компьютерной графики
3. Виды графического представления геометрических моделей. Цвет. Система RGB, CMYK.
4. Двумерные преобразования и новые координаты
5. Однородные координаты
6. Перенос и повороты в трехмерном пространстве
7. Основные принципы программирования Windows -приложения.
8. Разработка каркаса Windows –приложения.
9. Графические средства Windows API.
10.Перспективные изображения как результат центрального проецирования.
11.Видовое преобразование как аппарат построения аксонометрических изображений.
12.Перспективное преобразование и её проективная концепции.
13.Внутреннее компьютерное представления каркаса геометрической модели.
14.Основные принципы построения алгоритмов генерации простых геометрических объектов. Генерация файла для геометрического объекта «тор».
15. Основная концепция решения задач загораживания
16. Известные методы решения задач загораживания
17. Метод переборного типа
18. Метод Z-буфера
19. Удаление нелицевых граней многогранника
20. Математические способы приближения функции
21.Интерполяция точечного каркаса функции полиномами.
22.!Интерполяция сплайнами.
23.Построение В-сплайна.
24. Кривые Безье
25. Простая модель освещения
26.Определение нормали к поверхности.
27. Закраска методом Гуро
28. Закраска Фонга
10.Перспективные изображения как результат центрального проецирования.
Перспективные изображения
При необходимости
получения перспективной проекции
задаётся большое количество точек
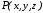 ,
принадлежащих объекту, для которых
предстоит вычислить координаты точек
изображения
,
принадлежащих объекту, для которых
предстоит вычислить координаты точек
изображения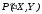 на картинке. Для этого нужно только
преобразовать координаты точки
на картинке. Для этого нужно только
преобразовать координаты точки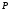 из так называемыхмировых
координат
из так называемыхмировых
координат
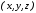 вэкранные
координаты
вэкранные
координаты
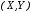 её центральной проекции
её центральной проекции
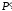 .
Будем предполагать, что экран расположен
между объектом и глазом
.
Будем предполагать, что экран расположен
между объектом и глазом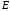 .
Для каждой точки
.
Для каждой точки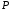 объекта прямая линия
объекта прямая линия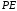 пересекает экран в точке
пересекает экран в точке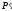 .
Это отображение удобно выполнять в два
этапа. Первый этап будем называтьвидовым
преобразованием
– точка
.
Это отображение удобно выполнять в два
этапа. Первый этап будем называтьвидовым
преобразованием
– точка
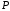 остаётся на своём месте, но система
мировых координат переходит в системувидовых
координат.
Второй этап называется перспективным
преобразованием.
Это точное преобразование точки
остаётся на своём месте, но система
мировых координат переходит в системувидовых
координат.
Второй этап называется перспективным
преобразованием.
Это точное преобразование точки
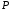 в точку
в точку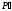 ,
объединённое с переходом из системы
трёхмерных видовых координат в систему
двухмерных экранных координат:
,
объединённое с переходом из системы
трёхмерных видовых координат в систему
двухмерных экранных координат: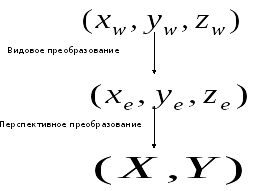
11.Видовое преобразование как аппарат построения аксонометрических изображений. Видовое преобразование
Для выполнения
видовых преобразований должны быть
заданы точка наблюдения, совпадающая
с глазом, и объект. Желательно, чтобы
система координат была правой. Будет
удобно, если начало её координат
располагается где-то вблизи центра
объекта, поскольку объект наблюдается
в направлении от
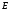 к
к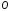 .
Предположим, что это условие выполняется.
Пусть точка наблюдения
.
Предположим, что это условие выполняется.
Пусть точка наблюдения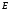 будет
задана в сферических координатах
будет
задана в сферических координатах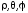 по отношению к мировым координатам. То
есть мировые координаты могут быть
вычислены по формулам:
по отношению к мировым координатам. То
есть мировые координаты могут быть
вычислены по формулам:
 (5.1.1)
(5.1.1)
Обозначение
сферических координат схематически
изображены на рис. 5.1.1. Говорят, что
вектор направления
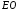 (равный
(равный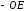 )
определяет направление наблюдения. Из
точки наблюдения
)
определяет направление наблюдения. Из
точки наблюдения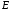 можно
видеть точки объекта только внутри
некоторого конуса, ось которого совпадает
с линией
можно
видеть точки объекта только внутри
некоторого конуса, ось которого совпадает
с линией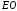 ,
а вершина – с точкой
,
а вершина – с точкой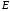 .
Если заданы ортогональные координаты
.
Если заданы ортогональные координаты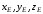 точки
точки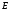 ,
то можно вычислить её сферические
координаты (п.4.5).
,
то можно вычислить её сферические
координаты (п.4.5).
Конечной задачей
является вычисление экранных координат
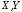 ,
для которых оси
,
для которых оси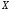 и
и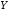 лежат в плоскости экрана, расположенной
между точками
лежат в плоскости экрана, расположенной
между точками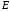 и
и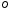 и перпендикулярной направлению наблюдения
и перпендикулярной направлению наблюдения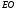 .
Начало системы видовых координат
располагается в точке наблюдения
.
Начало системы видовых координат
располагается в точке наблюдения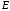 (рис.5.1.2). При направлении взгляда из
(рис.5.1.2). При направлении взгляда из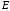 в
в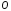 положительная полуось
положительная полуось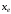 направлена вправо, а положительная
полуось
направлена вправо, а положительная
полуось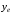 - вверх. Такое направление осей позволит
впоследствии определить экранные оси
в тех же направлениях. Направление оси
- вверх. Такое направление осей позволит
впоследствии определить экранные оси
в тех же направлениях. Направление оси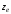 выбирается таким образом, что значения
координат увеличиваются по мере удаления
от точки наблюдения.
выбирается таким образом, что значения
координат увеличиваются по мере удаления
от точки наблюдения.
Видовое преобразование
может быть записано в форме
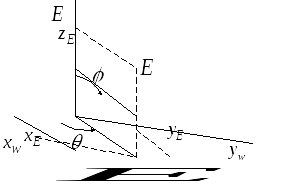
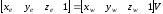 (5.1.2)
(5.1.2)
где
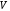 - матрица видового преобразования
размерностью
- матрица видового преобразования
размерностью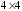 .
Для нахождения матрицы
.
Для нахождения матрицы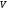 предположим, что преобразования
отображения могут быть составлены из
четырёх элементарных преобразований,
для которых легко написать свои матрицы
преобразований. Матрица
предположим, что преобразования
отображения могут быть составлены из
четырёх элементарных преобразований,
для которых легко написать свои матрицы
преобразований. Матрица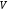 получается путём перемножения этих
четырёх матриц. Фактически каждое из
четырёх преобразований изменяет
координаты и, следовательно, определяется
матрицей, обратной матрице, соответствующей
преобразованию точки.
получается путём перемножения этих
четырёх матриц. Фактически каждое из
четырёх преобразований изменяет
координаты и, следовательно, определяется
матрицей, обратной матрице, соответствующей
преобразованию точки.
12.Перспективное преобразование и её проективная концепции. Перспективное преобразование
Далее мировые
координаты уже не будут затрагиваться.
Поэтому видовые координаты будут
обозначаться просто
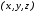 вместо
вместо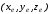 .
.
На рисунке 5.2.1
выбрана точка
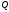 ,
видовые координаты которой равны
,
видовые координаты которой равны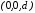 для некоторого положительного числа
для некоторого положительного числа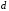 .
Плоскость
.
Плоскость определяет экран, который будем
использовать. Таким образом,экран
– это плоскость, проходящая через точку
определяет экран, который будем
использовать. Таким образом,экран
– это плоскость, проходящая через точку
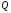 и перпендикулярная оси
и перпендикулярная оси .
Экранные координаты определяются
привязкой начала к точке
.
Экранные координаты определяются
привязкой начала к точке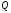 ,
а оси
,
а оси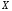 и
и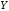 имеют такие же направления, как оси
имеют такие же направления, как оси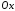 и
и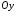 соответственно.
Для каждой точки объекта
соответственно.
Для каждой точки объекта точка изображения
точка изображения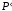 определяется как точка пересечения
прямой линии
определяется как точка пересечения
прямой линии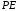 и экрана. Рассмотрим точку
и экрана. Рассмотрим точку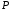 с нулевой
с нулевой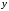 -
координатой. Треугольники
-
координатой. Треугольники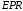 и
и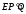 подобны. Следовательно,
подобны. Следовательно,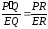 .
Отсюда будем иметь
.
Отсюда будем иметь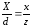 или
или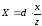 .
.
Аналогично можем
получить
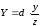 .
.
Поскольку ось
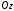 видовой системы координат совпадает с
прямой линией
видовой системы координат совпадает с
прямой линией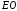 ,
которая пересекает экран в точке
,
которая пересекает экран в точке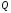 ,
то начало системы экранных координат
будет находиться в центре изображения.
Для переноса начала координат в левый
нижний угол с размерами экрана
,
то начало системы экранных координат
будет находиться в центре изображения.
Для переноса начала координат в левый
нижний угол с размерами экрана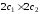 можно применить уравнения
можно применить уравнения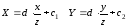 .
.
Исходное расстояние
 ,
помещающее весь объект в габариты
картинки можно определить из отношения:
,
помещающее весь объект в габариты
картинки можно определить из отношения:
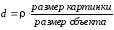 .
.
Рассмотрим общую
концепцию перспективного сокращения.
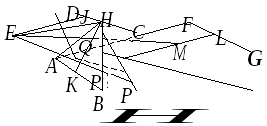
На
рисунке 5.2.2 изображены точки наблюдения
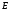 и экрана
и экрана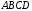 .
Взгляд направлен из точки
.
Взгляд направлен из точки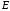 в точку
в точку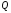 .
Прямые линии
.
Прямые линии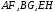 параллельны, и будем считать их
горизонтальными. Представим плоскость,
проходящую параллельные линии
параллельны, и будем считать их
горизонтальными. Представим плоскость,
проходящую параллельные линии и
и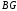 .
Эта плоскость пересекает плоскость
экрана по прямой линии
.
Эта плоскость пересекает плоскость
экрана по прямой линии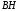 .
Таким образом, каждая точка
.
Таким образом, каждая точка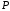 на прямой линии
на прямой линии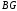 будет иметь свою центральную проекцию
будет иметь свою центральную проекцию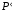 ,
лежащую на прямой
,
лежащую на прямой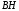 ,
при условии, что точка
,
при условии, что точка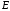 является центром проекции. Пусть точка
является центром проекции. Пусть точка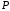 удаляется от точки
удаляется от точки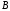 в бесконечность, тогда её проекция
в бесконечность, тогда её проекция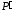 будет приближаться к точке
будет приближаться к точке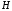 .
Это означает, что
.
Это означает, что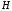 - точка схода для прямой линии, проходящей
через точки
- точка схода для прямой линии, проходящей
через точки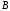 и
и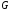 .
В терминах проективной геометрии точка
.
В терминах проективной геометрии точка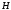 представляет собой проекцию бесконечно
удалённой точки, лежащей на прямой
представляет собой проекцию бесконечно
удалённой точки, лежащей на прямой
