
Анализ и решение
П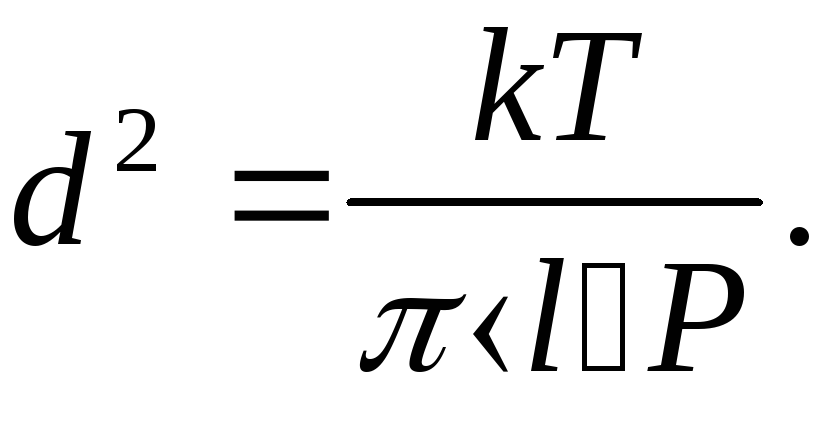 ри
нормальных условиях ( Р = 105Па
и Т = 273ОК)
водород можно с хорошей степенью
приближения считать подчиняющимся
уравнению состояния идеального газа,
то есть Р = nkT,
откуда легко определяется концентрация
молекул (постоянная Больцмана k
= 1,38х10-23
Дж/К). Осталось воспользоваться уравнением
(6.8), подставив в него концентрацию,
выраженную через давление и температуру,
и получаем для газокинетического
диаметра молекул зависимость
ри
нормальных условиях ( Р = 105Па
и Т = 273ОК)
водород можно с хорошей степенью
приближения считать подчиняющимся
уравнению состояния идеального газа,
то есть Р = nkT,
откуда легко определяется концентрация
молекул (постоянная Больцмана k
= 1,38х10-23
Дж/К). Осталось воспользоваться уравнением
(6.8), подставив в него концентрацию,
выраженную через давление и температуру,
и получаем для газокинетического
диаметра молекул зависимость
Подстановка численных значений из условий задачи дает для d = 3х10-10 м.
Необходимо помнить, что полученные численные значения справедливы с точностью до множителя порядка единицы.
Задача 6.2
Сколько столкновений за 1 секунду испытывает атом неона при давлении 100 Па и температуре 600 К, если известен его газокинетический диаметр d = 2∙10-10 м?
Анализ и решение
Для числа столкновений молекул газа в единицу времени имеется теоретическая формула (6.7) <z> = <v>nэф. Таким образом, для нахождения ответа на поставленный вопрос задачи следует по данным в условии задачи определить эффективное сечение рассеяния согласно формуле эф = d2, концентрации из уравнения состояния Р = nkT и средней скорости по формуле (5.5) <v> = (8kT/m)1/2. Подстановка соответствующих параметров в (6.7) дает
<z> = (8мkT)1/2 Pd2.
В этой формуле остается неизвестной масса одного атома неона, у которого атомное массовое число равно 20. Масса молекулы (атома) находится как обычно деление молярной массы М на известное число Авогадро NА = 6,02∙10231/моль. Теперь формула для вычисления числа столкновений атомов в единицу времени принимает вид
<z> = (8NA kT)1/2 Pd2.
Подстановка численных значений дает <z> = 1,3∙106с-1. Следует помнить, что все эти вычисления носят оценочный характер и справедливы только с точностью до коэффициента порядка единицы. Поэтому корректный ответ: число соударений молекулы в секунду – порядка 106.
Задача 6.3
Как изменится вязкость идеального газа, если его объем уменьшить в два раза: а) изотермически; б) изобарически.
Анализ и решение
М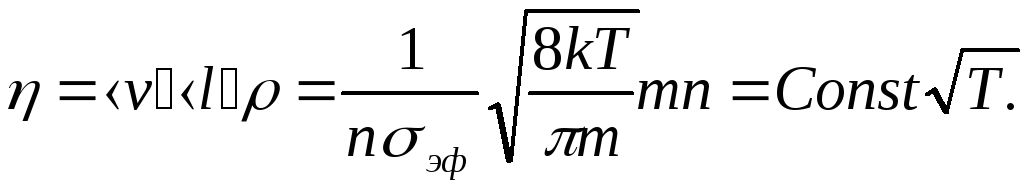 одельное
рассмотрение поведения газа на микроуровне
дает теоретическую зависимость вязкости
газа от микропараметров (6.5). Это позволяет
с учетом зависимости средней длины
свободного пробега от концентрации
(6.8) и выражения (5.5) для средней скорости
молекул (а также при замене плотности
газа на произведение массы одной молекулы
на концентрациюmn)
увидеть, от каких параметров зависит
вязкость газа, а именно
одельное
рассмотрение поведения газа на микроуровне
дает теоретическую зависимость вязкости
газа от микропараметров (6.5). Это позволяет
с учетом зависимости средней длины
свободного пробега от концентрации
(6.8) и выражения (5.5) для средней скорости
молекул (а также при замене плотности
газа на произведение массы одной молекулы
на концентрациюmn)
увидеть, от каких параметров зависит
вязкость газа, а именно
Эта формула показывает, что вязкость газа изменяется только при изменении температуры, вне зависимости от изменения давления или объема (если это не связано с изменением температуры). Отсюда вывод: в изотермических процессах вязкость газа остается неизменной. Это ответ на первый вопрос задачи.
При изобарном процессе расширения газа (Р = Const) для сохранения давления при уменьшении объема необходимо понижать температуру газа согласно уравнению изобары для идеального газа V1/T1 = V2/T2 .
С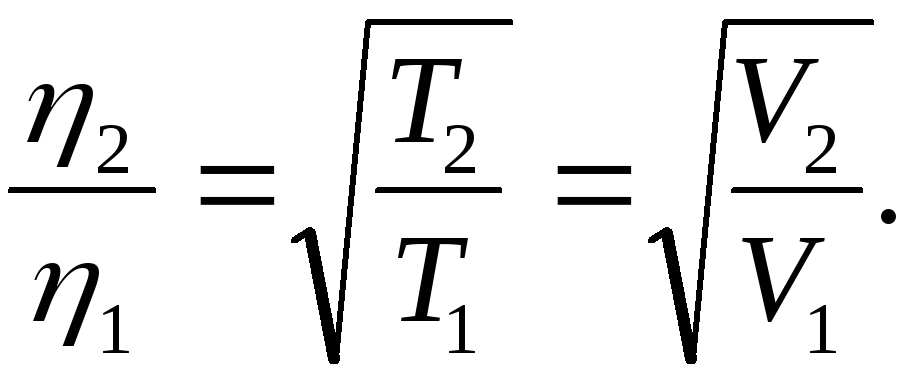 ледовательно,
ледовательно,
Отсюда очевиден ответ на второй вопрос задачи - изобарное уменьшение объема газа в два раза приведет к уменьшению температуры в два раза и, соответственно, к уменьшению вязкости газа в корень квадратный из двух.
Дополнительные вопросы
Перенос каких величин рассматривается в процессах переноса и как называются соответствующие процессы?
От каких микроскопических параметров зависят коэффициенты диффузии, динамической вязкости и теплопроводности в газах?
Попытайтесь ответить на вопрос: Каков смысл выкачивания воздуха между стенками сосуда Дьюара (термоса), если теплопроводность газа (как и его вязкость) не зависит от плотности газа, то есть от концентрации молекул, что видно из решения задачи 6.3?
Рекомендуемая литература
Сивухин Д.В. Общий курс физики, Термодинамика и молекулярная физика.- М.: Наука, 1975, Т.2.
Сборник задач по общему курсу физики /Под ред. Д.В.Сивухина/.- М.: Наука, 1976.
Ландау Л.Д., Ахиезер А.И., Лифшиц Е.М. Курс общей физики: Механика и молекулярная физика.- М.: Наука, 1965.
