№14. Тригонометрическая и показательная формы

Если вещественную  и мнимую  части комплексного числа выразить через модуль  и аргумент  (, ), то всякое комплексное число , кроме нуля, можно записать в тригонометрической форме

Также может быть полезна показательная форма записи комплексных чисел, тесно связанная с тригонометрической через формулу Эйлера:

где  — расширение экспоненты для случая комплексного показателя степени.

Отсюда вытекают следующие широко используемые равенства:

№15. Формула Муавра и извлечение корней из комплексных чисел

Корни пятой степени из единицы(вершины пятиугольника)

Эта формула позволяет возводить в целую степень ненулевое комплексное число, представленное в тригонометрической форме. Формула Муавра имеет вид:

где  — модуль, а  — аргумент комплексного числа. В современной символике она опубликована Эйлером в 1722 году. Приведенная формуле справедлива при любом целом n, не обязательно положительном.

Аналогичная формула применима также и при вычислении корней -ой степени из ненулевого комплексного числа:

Отметим, что корни -й степени из ненулевого комплексного числа всегда существуют, и их количество равно . На комплексной плоскости, как видно из формулы, все эти корни являются вершинами правильного -угольника, вписанного в окружность радиуса  с центром в начале координат (см. рисунок).

№16. извлечение корней n-ной степени комплексных чисел

Вапв

Вап

Ва

№17. . Алгебраические уравнения, теорема Гаусса.

Алгебраическое уравнение — уравнение, получающееся при приравнивании двух алгебраических выражений.

Алгебраическое выражение — выражение, составленное из букв. Чисел, скобок, соединенных знаками алгебраических операций: +, -, *, :, возведение в степень, извлечение корня.

Примеры алгебраических уравнений:

X²+XY+Y²-X+1=0 ;   =2

 Алгебраическое уравнение с одним неизвестным может быть преобразовано к виду (1):

a₀ + a₁x + a₂x² + …+ a_nxⁿ = 0

Способы решения таких уравнений первой и второй степени известно еще из древности. В XVI в. были найдены способы решения уравнений третьей и четвертой степени.

Основная теорема алгебры (теорема Гаусса).

Любое алгебраическое уравнение (1) степени N имеет N решений (корней) действительных или мнимых, если каждый корень считать столько раз, какова его кратность.

Корень многочлена  a₀ + a₁x + a₂x² + …+ a_nxⁿ  ( a_n0) — это число z₀, такое, что:

a₀ + a₁ z + a₂ z² + …+ a_n zⁿ = 0

Свойство корня:

Число z₀ — корень (1)  многочлен (1) можно представить в виде

 

(x - z₀) (b₀ + b₁x + b₂x² + …+ b_n-1x^n-1),

 то есть (1) делится на (x - z₀)  без остатка.

Если  (1) делится на (x - z₀)^k, но не делится на (x - z₀)^k+1, то z₀ называется корнем кратности k, при этом

(x - z₀)^k (b₀ + b₁x + b₂x² + …+ b_n-kx^n-k).

Доказано, что решения уравнений степени выше четвёртой нельзя выразить через коэффициенты уравнения при помощи алгебраических действий.

№ 18. Разложение многочленов на множители

Тождественное преобразование, приводящее к произведению нескольких множителей - многочленов или одночленов, называютразложением многочлена на множители. В этом случае говорят, что многочлен делится на каждый из этих множителей.

Вынесение общего множителя за скобки. Это преобразование является непосредственным следствием распределительного закона ac + bc = c(a + b)

Пример. Разложить многочлен на множители 12 y ³ – 20 y ². Решение. Имеем: 12 y ³ – 20 y ² = 4 y ² · 3 y – 4 y ² · 5 = 4 y ² (3 y – 5). Ответ. 4 y ²(3 y – 5).

Использование формул сокращенного умножения. Формулы сокращённого умножения позволяют довольно эффективно представлять многочлен в форме произведения.

Пример. Разложить на множители многочлен x ⁴ – 1. Решение. Имеем: x ⁴ – 1 = ( x ² ) ² – 1 ² = ( x ² – 1)( x ² + 1) = ( x ² – 1 ² )( x ² + 1) = ( x + 1)( x – 1)( x ² + 1).Ответ. ( x + 1)( x – 1)( x ² + 1).

Способ группировки. Этот способ заключается в том, что слагаемые многочлена можно сгруппировать различными способами на основе сочетательного и переместительного законов. На практике он применяется в тех случаях, когда многочлен удается представить в виде пар слагаемых таким образом, чтобы из каждой пары можно было выделить один и тот же множитель. Этот общий множитель можно вынести за скобку и исходный многочлен окажется представленным в виде произведения.

Пример. Разложить на множители многочлен x ³ – 3 x ² y – 4 xy + 12 y ². Решение. Сгруппируем слагаемые следующим образом:  x ³ – 3 x ² y – 4 xy + 12 y ² = ( x ³ – 3 x ² y ) – (4 xy – 12 y ² ). В первой группе вынесем за скобку общий множитель x ², а во второй − 4 y . Получаем:  ( x ³ – 3 x ² y ) – (4 xy – 12 y ² ) = x ² ( x – 3 y ) – 4 y ( x – 3 y ). Теперь общий множитель ( x – 3 y ) также можно вынести за скобки:  x ² ( x – 3 y ) – 4 y ( x – 3 y ) = ( x – 3 y )( x ² – 4 y ). Ответ. ( x – 3 y )( x ² – 4 y ).

Способ выделения полного квадрата. Метод выделения полного квадрата является одним из наиболее эффективных методов разложения на множители. Суть его состоит в выделении полного квадрата и последующего применения формулы разности квадратов.

Пример. Разложить на множители многочлен x ⁴ + 4 x ² – 1. Решение. Имеем x4+4x2−1=x4+22x2+4−4−1=(x2+2)2−5=(x2+2−5)(x2+2−5) .

№19. Деление многочлена

Покажем, что

Частное и остаток от деления могут быть найдены в ходе выполнения следующих шагов:

1. Делим первый элемент делимого на старший элемент делителя, помещаем результат под чертой .

2. Умножаем делитель на полученный выше результат деления (на первый элемент частного). Записываем результат под первыми двумя элементами делимого .

3. Вычитаем полученный после умножения многочлен из делимого, записываем результат под чертой .

4. Повторяем предыдущие 3 шага, используя в качестве делимого многочлен, записанный под чертой.

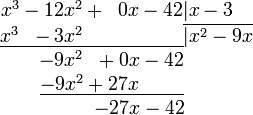
5. Повторяем шаг 4.

6. Конец алгоритма.

Таким образом, многочлен  — частное деления, а  — остаток.

№20. Теорема Безу.

Теорема Безу утверждает, что остаток от деления многочлена  на двучлен  равен .

Предполагается, что коэффициенты многочлена содержатся в некотором коммутативном кольце с единицей (например, в поле вещественных или комплексных чисел).