Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Магнитогорский государственный технический университет им. Г.И.Носова

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Uchebnye_karty_Chast1

.pdf

Скачиваний:

Добавлен:

11.02.2015

Размер:

778.78 Кб

Скачать

☆

<<< < Предыдущая 1 2 34 / 44

26. Непрерывность

функции

Определение

непрерывности

функции

Свойства непрерывных функций на отрезке[a, b]

1. y=f(x) непрерывна в т. х0

Если функция y=f(x) непрерывна на отрезке [a, b], то:

а) f(x) определена в т. х0 и в ее окрестности;

1. f(x) ограничена на отрезке [a, b]:

2. α,β [a,b] : f (α) ≤ f (x) ≤ f (β) x [a,b]

f (x) = f (β) = M

б)

lim

f (x) = f (x ) = A(A≠ ∞)

max

(наибольшее значение f);

x [a,b]

x→x0

min

f (x) = f (α) = m

(наименьшее значение f);

y = f (x0 +

x) − f (x0 )

x [a,b]

f(в)

f(x0 + x)

y = 0

l i m

Замечание:Вчастностиможет:

α = a, α = b;

β = a,β = b

( x0 )

x →0

f(а)

x0 + x

c [a, b] : f (c) = 0, если

f (a) f (b) < 0

-k

Условиенепрерывностифункции

y = f (x)вт.x

lim

f (x) = f (x )

x→x

Классификация разрывов функции в т.х0

Разрывы I рода

Разрывы II рода

т.х0 - точка устранимого разрыва

т.х0 - точка разрыва со скачком

т.х0 - точка бесконечного разрыва

Функция в т. х0 - не определена

Функция в т. х0 - определена

Функция в т. х0 - не определена

или слева, или справа

или

lim

f (x) = lim

f (x) = A

х0

x→x0 +

x→x0

−

х0

Доопределение

функции

y = f (x)

f (x), если x < x

0 ,

lim

f (x) = +∞

lim

f (x) = A

x→x0 − 0

x→x0 + 0

y = f (x0 ), если x = x0 ,

lim

f (x) = A,

lim f (x) = B

lim

f (x) = −∞

lim

f (x) = +∞

f (x), если x > x

x→x0− 0

x→x0 + 0

x→x

−

x→x0 + 0

lim

f (x) ≠ lim f (x)

x→x0− 0

x→x0+ 0

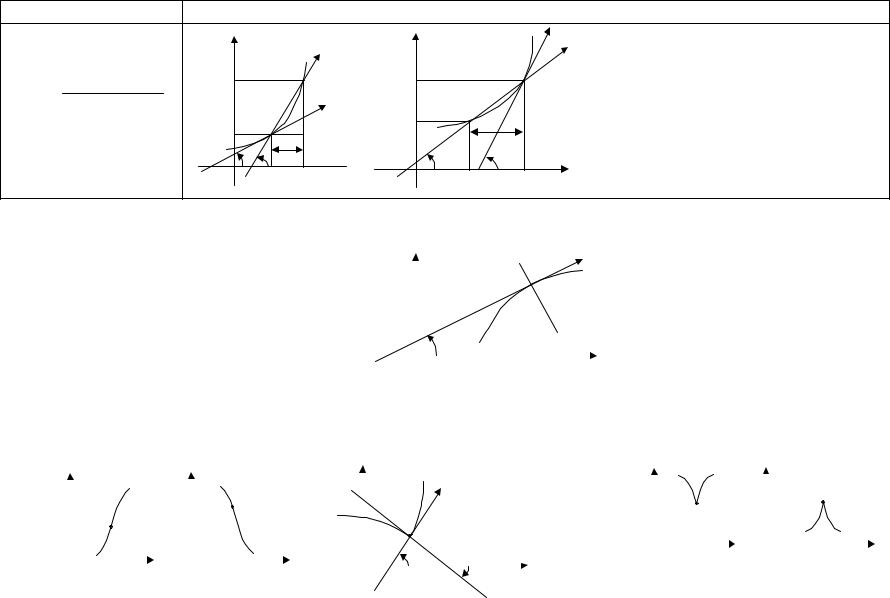
27. Производная функции y=f(x)

Определение

Геометрический

смысл

производной в т. х0

AS - секущая, АТ - касательная в т. А

При

x → 0:β → α;tgβ → tgα

f(x + x)

f (x +

x) − f (x)

f(х

tg α = k

-угловойкоэффициент

y' = lim

кас

касательной АТ к кривой

x→0

f(x0 +

y = f (x) в т. A(x0, y0 )

= lim

f(х0)

x→0

α β

f '(x0) = lim

y = kкас

х0 x0 + x

x0 + x

x→0

х0

Приложенияпроизводнойвгеометрии

Задача

Данные

Геометрическаяиллюстрация

Указания к решению

a) y = f (x);

Уравнения касательной

(AT ) : y − y0 = f

(x0)(x − x0);

A (x0, y0 );

и нормали к графику функции

б) y = f (x );

( AN ) : y − y0 = −

(x − x

0 )

kкас

f ' (x

)

х0

Условиедифференцируемостифункциивт.х :

) = f

' (x

)

пр

Случаинедифференцируемойфункциивт.х0

т. A(x0 , y0 )- точка перегиба с вертикальной касательной

т. A (x

, y

) - угловая точка

т. A(x

, y

) - точка

возврата

(x0 ) = tg α1 =

lim

x →0

x< 0

) = tg α

lim

пр

x→0

x> 0

х0

х 0

х0

f ' (x ) = −∞

fл' (x0) = +∞

> 0

< 0 х

f '(x0 ) = +∞

f '(x0 ) = −∞

(x0 ) = +∞

(x0 ) = −∞

пр

28. Таблица производных и правила дифференцирования

Элементарныефункции

Сложные функции

a = const

(a)' = 0

(xn ) = nxn−1;

n n−1

= u

;

Степеннаяфункция

= −

;

=−

;

(

)'=

(

)' =

2 x

Показательная

(ax )' = ax ln a;

(au )'

= au ln a u';

функция

(ex )' = ex;

(eu )'

= eu u'

(sin x)' =cos x;

(sin u)' = u'cos u;

(cos x)'

= −sin x;

(cos u)=− u sin u;

Тригонометрические

(tg x)' =

(tg u)

;

cos 2 u

функция

cos 2 x

= −

−1

(ctg u)

(ctg x)'

;

sin

sin2

Логарифмические

(log a x)' =

;

(log a u)'

;

x ln a

u ln a

функция

(l n x)' =

(l n u)'

= u'

(arctg x)

' =

;

(arctgu)' =

;

+ x

1+ u

Обратные

(arcctg x)' =

-1

;

(arcctgu)'=−

;

+ u2

тригонометрические

1+ x

функции

(arcsin

x)'

;

(arcsin

;

1− x2

1 − u2

(arccos

x)=−

;

(arccos

=−

;

1− x2

1− u2

(sh x)' = chx;

(shu)' = chu u';

Гиперболические

(ch x)' = sh x;

(chu)' = shu u';

функции

(th x)' =

;

(thu)' =

u';

(cthx)' =

− 1

;

(cth u)' =

− 1

u';

Степенно-

(uv)'

= uv ln u v' + vuv−1 u'

показательныефункции

Параметрические

x = x(t)

y''

( y'

y''x'

− x

''y'

функции

; y

;

x t

y = y(t)

' )3

Правила

(u ± v)' = u ± v

'; u

u'v − v

;

(u v)

= u

+ v

дифференцирования

(cu)

= cu

	Дифференциал			функции
Определение	Функция f(x) называется дифференцируемой
	Функция f(x) называется дифференцируемой							x) = 0
дифференцируемой	в точке х, если		y =	A(x) x		+ α (	x) , где lim α(	x) = 0
функции в точке х							x→0	x
							x→0	x
Необходимое и	y = A(x)		x + α(		x) f (x)		имеет конечную
достаточноеусловие	производную		f '(x) в этой точке.
дифференцируемости	Итогда A(x) = f '(x)
функции в точке х	Итогда A(x) = f '(x)
	A(x)	x = f '(x)		x - главная, линейная
Определение	относительно		x , часть приращения
Определение	функции называется дифференциалом
дифференциала	функции называется дифференциалом
дифференциала	dy функции f (x)
функции и обозначение	dy функции f (x)
функции и обозначение	dy = f ' (x)dx, где				dx =
	dy = f ' (x)dx, где				dx =	x - дифференциал
	независимой переменнойх.
	y		B			ADC : CD = tg α		x
			B		T	ADC : CD = tg α		x
Геометрический смысл				D	T	CD = f ' (x) x = dy
дифференциала		A	α			dy = CD - приращение
функции		A				ординаты касательной АТ
функции				C		ординаты касательной АТ
			x	C
	α		x
	α
	0	x	x+	x	x

Приложения дифференциала

№

Задача

Дано

Указание к решению

Найти приращение

y = f (x); x0 ; x

y ≈ dy

функции

Найтизначение

f (x

+ x) ≈ f (x

) + dy (x

функции

f(x +

dy(x

) = f ' (x

) x

где

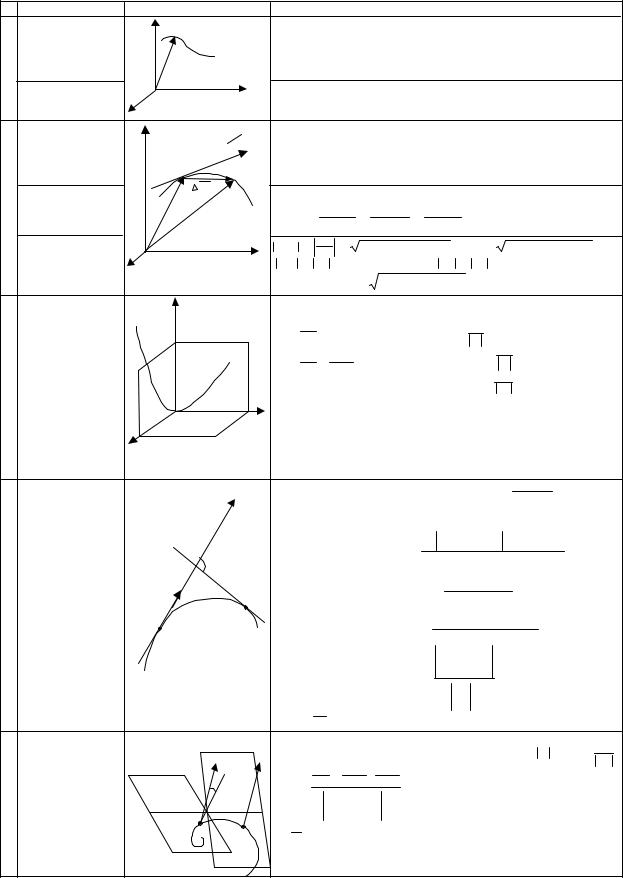
29. Вектор - функция скалярного аргумента

Понятие

Графическаяинтерпретация

Определение,вычисление,свойства

M (x,y,z)

x = x(t )

Вектор -функция

= y(t )

КаждомуtсоответствуетR R векторR

Задача: L: y

скалярного

= z(t )

r(t) = x( )i + y(t) j + z(t)k

аргументаt

t - параметр, определяющий вектор-функцию

r (t )

Годограф

Линия L - описываемая концом вектора

r (t)- годограф.

M (x, y, z) L, такчто

x = x(t );

y = y(t );

z = z(t)

вектор-функции

= lim

= x

+ y

Производная

(t)i

(t)k

r(t)

(t) j

+ z

вектор-функции

→0

R t)

(

r(t) = T

- вектор, направленныйR

по касательной к годографу

радиус-вектора r (t) в сторону возрастания параметра

Касательная в т. М

, y , z

) L, x0

= x(t0 );

=y(t0 );

z0 = z(t0 )

r (t

)

− y0

z − z0

к годографу

− x0

вектор-функции

r (t0 +

x'(t

)

y' (t

)

z'(t

)

)xt' )2

+)yt')2 +)zt')2

)xt')2 +)yt')2 +)zt')2 dt

r (t)

Дифференциал

r ~

l приM0 → M1 dr = dl

дуги dl

dl = x ')2

y')2 + z

')2 dt

)

главная

M ( x ,

y , z ) L

можносопоставитьтривзаимно

нормаль

перпендикулярныхвектора:

d r

-тангенциальный

-векторкасательной;

единичныйвектор.

сопрякасающаяся

- орт бинормали;

ьна

плоскость

d r

-векторбинариали;

β =

Сопровождающий

ал т

кос

рм с

но о

-орт

трехгранник

пл

линии L

N =

B × T-вектор главнойнормали;

гл. нормали.

касательная

B = ( B x ,

= (

N y , N z )

(триэдр)

(T x , T y , T z

B y ,

B z

N x ,

спрямляющаяτ

Tx ( x − x0 )

+ Ty ( y − y0 ) + T z ( z − z 0 )

= 0 - пл. нормальная;

плоскость

бинормаль

Bx (x − x0 ) + B y ( y − y0 )

+ Bz ( z − z0 ) = 0

- пл. соприкасающаяся;

N x ( x − x0 )

+ Ny ( y − y0 ) + N z ( z − z0 ) = 0 - пл. спрямляющая;

ϕ -уголсмежностикривой

L : K =

lim

-угловая

M 0 → M 2

скорость вращения касательного вектора

τ в точке М0

КривизнаК

x = x(t)

K =

yt''xt'

− yt'

xt''

плоской и

L :

= y(t)

)

3/ 2

пространственнойк

(( xt

( yt

(zt )

y11

ривой L.

L : y = y ( x ),

K =

Радиус

(1+(y')2)3 / 2

кривизны R.

ρ2

+2)ρ')2

− ρ ρ

КривизнаК

L :ρ = ρ(ϕ),

K =

характеризует

(ρ2

+(ρ')2)3 / 2

степеньотклонения

x = x(t )

d2r

линии от прямой

L : y = y(t ),

K =

3 .

z = z(t )

= R - радиус кривизны

Кручение

Кручение - это предел отношения угла поворота бинормали на

дуге, стягивающейся к точке, к длине этой дуги;

σ = l i m

пространственной

l→0

кривой L.

× d

Радиус кручения ρ .

σ =

dt 2

dt 3

- угловая скорость вращения

Кручение σ

в точке М0

dr × d 2 r

вектора

характеризуетстепень

отклонениялинии

= ρ - радиус кручения

отсоприкасаю-

щейся плоскости

30. Полное исследование функции и построение графиков

№

Алгоритм исследования функции f(x)

Найти область

10.Выделить точки разрыва функции.

1)Точки разрыва определяют интервалы

определенияфункции,

20.Определить тип разрыва, найдя односторонние

непрерывности функции.

определитьчетность,

2) Если

f (− x) = ± f ( x )

пределы

,0то нужно исследовать

периодичность

функцию только при x>0.

10.х=а - вертикальная асимптота графика функции,

1) Если k=0,то y=b- горизонтальная асимптота:

если х= а - точка разрыва II рода и

2)Приопределенииасимптотграфикафункции

Определитьасимптоты

l i m f (x) = ±∞ или

l i m f (x) = ±∞

пределы приx → +∞ и x → −∞ могут быть

графикафункции

x→ a - 0

x→a +0

различными, поэтомунужно искатьоба предела.

20.y=kx+b - наклонная асимптотаграфика функции,

если k = l i m

f (x)

; b =l i m ( f (x) − kx)

3)Наклоннаяасимптотаможетпересекать

графикфункции

x→±∞

10. Найти y’, разложить на множители.

1)Критическимиточкамифункциимогутбыть

20. Найти критические точки функции по первой

тольковнутренниеточкиобластьопределения.

производной(y

= 0 или

2)Знак y’на интервале монотонности может

y = ∞)

30. Разбив числовую ось критическими и граничными

быть определен по ее знаку в произвольной

точками (точками разрыва), определить знакy’ в

точкеэтогоинтервала.

Определитьинтервалы

каждоминтервалемонотонности.

Если y’=0

в т. x=x0

40.Найти ymin , ymax

y'>0

монотонностии

y'>0

y'<0

экстремумыфункции

max

min

4) Если

y' = ∞ в т. x=x0

y'>0 В

y'<0

y'>0

maxx0

min

		10.Найти y,''разложить ее на множитель.	А(x ,y ) -точка перегиба
				0	0
		20.Найти критические точки функций по второй			y''<0	y''>0		y''>0
		производной( y '' = 0 или y'' = ∞ )			y''<0			y''>0
	Определитьинтервалы	производной( y '' = 0 или y'' = ∞ )				A		A
	Определитьинтервалы	30.Разбив числовую ось критическими и граничными	A	y'' =∞		A		A
4	выпуклости(вогнутости)	30.Разбив числовую ось критическими и граничными	A	y'' =∞		y''=0
		точками, определить знак, y''в каждом интервале				y''=0		y''=0
		точками, определить знак, y''в каждом интервале				y''<0		y''=0
	и точки перегиба	выпуклости (вогнутоcти).	y''>0			y''<0		y''<0
	графикафункции	выпуклости (вогнутоcти).	y''>0					y''<0
	графикафункции	40.Найти значение функции в точкахперегиба.		x0	x	x0	x	x0	x
		50.Определить значения y’ вточке перегиба для о		x0	x	x0	x	x0	x
		пределения направления касательной в точке перегиба	касательная			касательная		касательная
		( y'(x0 ) = tg α кас )	вертикальная			наклонная		горизонтальная

1.Замечание. Для построения графика функции не всегда нужно проводить полное исследование функции

31. Графическое дифференцирование функции y=f(x), заданной графиком

№	Алгоритм	Поведение графика функции y=f(x)		Поведение графика производной y=f'(x)
		в системе XOY		в системе XOY'

1	Выделить	a)f(x) имеет вертикальную асимптоту x=a;	y'несуществует:	a) f’(x) имеет вертикальную асимптоту x =a;
	асимптотыграфика	б)f(x) имеет горизонтальную асимптотуx=b;	y' =0	б) f’(x) имеет горизонтальную асимптоту	y '= 0;
	функции	в) f(x) имеет наклонную асимптоту y=kx+b	y'=k	в) f’(x) имеет горизонтальную асимптоту	y '= k

		a) в т. x = x1 экстремум с горизон-					y' =0	a) f’(x) пересекает ось OX в. т. X= X1;
		тальной касательной;
	Выделить	б) в т. x = x2 экстремум с верти-	x1		x1	x	y' = ∞	б)f’(x)имеетвертикальнуюасимптоту
2	точки экстремума	кальной касательной;						X= X2;
2	точки экстремума							X= X2;
	функции	в) в т. x= x3 экстремум с		x2	x2	x		в) f’(x) имеет разрыв первого рода
		двумякасательными						(скачок)
		(угловаяточка)					y' несуществует
		x3			x3	x	y' несуществует
		x3			x3	x

а) в т. x = x4 перегиб с

y'' = ∞

вертикальнойкасательной;

Выделить точки

a) f’(x)

имеет вертикальную

асимптоту x=x5;

перегиба графика

б) в т. x= x

перегиб с

y'' =0

б) f’(x)

в т. (x , tg

) имеет

экстремум;

функции

наклоннойкасательной;

в) в т. x= x6

перегиб с

в) f'(x)

в т. (x6, 0)

имеет экстремум

горизонтальнойкасательной	x	y'' =0
x	x	y'' =0
6

Выделитьинтервалы

а)f(x)возрастаетна(a,b);

y'>0 на(a,b)

а) f’(x) на (a,b) расположен над осью 0Х;

монотонности

б)f(x) убываетна(a,b)

y'<0 на(c,d)

б) f’(x) на (c,d) расположен над осью 0Х

Выделить интервалы

а)f(x) выпуклыйна(a1,b1);

y'' <0

а) f’(x) на (a1,b1) убывает;

5 выпуклости и вогнуто-

б)f(x) вогнутые на(с1,d1)

y'' >0

б) f’(x) на (c1,d1) возрастает

сти

графика функции

Построение точки

(x0,y)

графика f ’(x) по

точке графика f(x)

x = x0

(x ,

<<< < Предыдущая 1 2 34 / 44

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
16.11.2019246.27 Кб7Tx_1_Dec_Zan.doc
#
16.11.2019190.46 Кб2Tx_3_Dec_Zan.doc
#
16.11.2019250.37 Кб5Tx_5_ Dec_Zan.doc
#
31.07.20192.3 Mб27TYeHNOLOGIChYeSKIJ_PROTsYeSS_PROIZVODSTVA_SLYaB....doc
#
20.11.20191.81 Mб301Uchebnoe_posobie_po_okhrane_truda.doc
#
11.02.2015778.78 Кб60Uchebnye_karty_Chast1.pdf
#
11.02.20151.24 Mб39Uchebnye_karty_Chast_2.pdf
#
01.07.2025432.64 Кб0UHEBNIK_oficiant.doc
#
27.11.2019482.3 Кб45UMK_GMU.doc
#
11.02.20156.48 Mб54Untitled.FR11.doc
#
16.12.2018149.5 Кб78upravlenie_personalom_kursovaya_rabota_2011.doc