
- •3 Расчетно-конструктивный раздел
- •3.1.4 Сбор нагрузки на панель перекрытия
- •3.1.5 Характеристики материалов для проектирования панели
- •3.1.6 Подбор напрягаемой арматуры
- •3.1.7 Определение геометрических характеристик приведенного сечения панели
- •3.1.8 Определение потерь предварительного напряжения
- •3.1.9 Расчет прочности наклонных сечений на действие поперечных сил
- •3.1.10 Расчет по образованию нормальных трещин
- •3.1.11 Расчет по раскрытию нормальных трещин
- •3.1.12 Определение прогиба панели
- •3.2 Расчет сборного железобетонного марша
- •3.2.1 Исходные данные
- •3.2.2 Определение нагрузок и усилий
- •3.2.2 Предварительное назначение размеров сечения марша
- •3.2.3 Подбор сечения продольной арматуры
- •3.2.4 Расчет наклонного сечения на поперечную силу
- •3.3 Расчет железобетонной площадочной плиты
- •3.3.1 Исходные данные
- •3.3.2 Определение нагрузок
- •3.3.3 Расчет полки плиты
- •3.3.4 Расчет лобового ребра
- •3.3.5 Расчет наклонного сечения лобового ребра на поперечную силу
3.1.12 Определение прогиба панели
Расчет изгибаемых элементов по прогибам производят из условия:
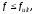
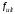 -
значение предельно допустимого прогиба.
-
значение предельно допустимого прогиба.
Нагрузки,
от которых определяется прогиб,
принимаются с коэффициентами
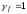 и
и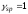 ,
а расчетное сопротивление материалов
– дляII-ой
группы предельных состояний.
,
а расчетное сопротивление материалов
– дляII-ой
группы предельных состояний.
При
действии постоянных, длительных и
кратковременных нагрузок прогиб балки
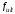 или плит во всех случаях не должен
превышать
или плит во всех случаях не должен
превышать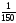 пролета.
пролета.
Для свободно опертых или консольных элементов максимальный прогиб определяют по формуле:
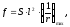
где
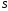 - коэффициент, зависящий от расчетной
схемы элемента и вида нагрузки, принимаемый
при действии равномерно распределенной
нагрузки равным
- коэффициент, зависящий от расчетной
схемы элемента и вида нагрузки, принимаемый
при действии равномерно распределенной
нагрузки равным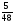 - для свободно опертой балки.
- для свободно опертой балки.
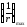 -
полная кривизна в сечении с наибольшим
изгибающим моментом от нагрузки, при
которой определяют изгиб.
-
полная кривизна в сечении с наибольшим
изгибающим моментом от нагрузки, при
которой определяют изгиб.
Определение кривизны изгибаемых предварительно напряженных элементов.
Полная кривизна изгибаемых предварительно напряженных элементов с трещинами в растянутой зоне определяется по формуле:
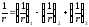 ,
,
где
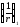 - кривизна от непродолжительного действия
всей нагрузки, на которую производят
расчет по деформациям;
- кривизна от непродолжительного действия
всей нагрузки, на которую производят
расчет по деформациям;
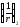 -
кривизна от непродолжительного действия
постоянных и временных длительных
нагрузок;
-
кривизна от непродолжительного действия
постоянных и временных длительных
нагрузок;
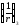 -
кривизна от продолжительного действия
постоянных и временных длительных
нагрузок.
-
кривизна от продолжительного действия
постоянных и временных длительных
нагрузок.
Кривизну изгибаемых предварительно напряженных элементов допускается определять по формуле:
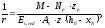
где
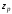 -
расстояние от точки приложения усилия
предварительного обжатия до точки
приложения равнодействующих усилий в
сжатой зоне;
-
расстояние от точки приложения усилия
предварительного обжатия до точки
приложения равнодействующих усилий в
сжатой зоне;
z – расстояние от центра тяжести растянутой арматуры до точки приложения равнодействующей усилий в сжатой зоне;
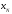 -
высота сжатой зоны с учетом влияния
предварительно обжатия.
-
высота сжатой зоны с учетом влияния
предварительно обжатия.
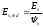 -
приведенный модуль деформации растянутой
арматуры, определяемый с учетом влияния
работы растянутого бетона.
-
приведенный модуль деформации растянутой
арматуры, определяемый с учетом влияния
работы растянутого бетона.
Значения
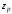 иz
допускается определять, принимая
расстояние от точки приложения
равнодействующей усилий в сжатой зоне
до наиболее сжатого волокна сечения
равным
иz
допускается определять, принимая
расстояние от точки приложения
равнодействующей усилий в сжатой зоне
до наиболее сжатого волокна сечения
равным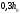 .
.
Таким
образом, величина
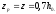
Для тавровых и двутавровых сечений высоту сжатой зоны без учета предварительного напряжения определяют по формуле:
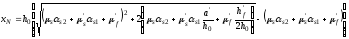 где
где
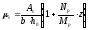 ,
,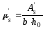 ,
,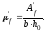
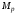 -
момент относительно центра тяжести
полного приведенного сеения элемента
от внешней нагрузки M
и усилия предварительного обжатия
-
момент относительно центра тяжести
полного приведенного сеения элемента
от внешней нагрузки M
и усилия предварительного обжатия
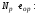
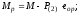
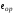 -
эксцентриситет усилия обжатия бетона
-
эксцентриситет усилия обжатия бетона
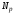 относительно центра тяжести полного
приведенного сечения элемента (без
учета моментаМ).
относительно центра тяжести полного
приведенного сечения элемента (без
учета моментаМ).
Значения коэффициентов приведения арматуры к бетону принимают равными:
-
для сжатой арматуры
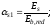
-
для растянутой арматуры
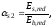
где
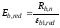 - приведенный модуль деформации сжатого
бетона при непродолжительном и
продолжительном действии нагрузки;
- приведенный модуль деформации сжатого
бетона при непродолжительном и
продолжительном действии нагрузки;
Значения
относительных деформаций
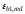 принимают при непродолжительном действии
нагрузки
принимают при непродолжительном действии
нагрузки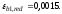
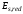 -
приведенный модуль деформации растянутой
арматуры, определяемый с учетом влияния
работы растянутого бетона между трещинами
по формуле
-
приведенный модуль деформации растянутой
арматуры, определяемый с учетом влияния
работы растянутого бетона между трещинами
по формуле
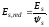 Значения коэффициента
Значения коэффициента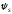 допускается принимать равным1 и
следовательно
допускается принимать равным1 и
следовательно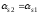 .
.
Определение прогиба
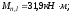
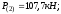
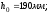
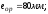
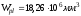
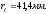
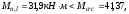
Приведенный модуль деформации сжатого бетона:
- при непродолжительном действии нагрузки
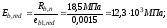
- при продолжительном действии нагрузки
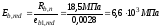
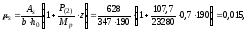
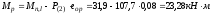
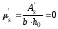 ,
,
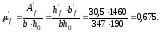
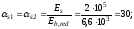
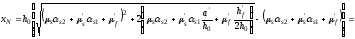
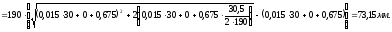 Кривизна
от продолжительного действия постоянных
и длительных нагрузок равна:
Кривизна
от продолжительного действия постоянных
и длительных нагрузок равна:
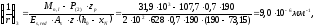
где
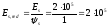 .
.
Максимальный прогиб в середине пролета равен:
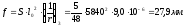 <
<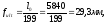
Следовательно жесткость плиты обеспечена.
