Задача 2

Через прямую DE провести плоскость, перпендикулярную плоскости треугольника АВС. Построить линию переселения этик плоскос­тей и определить их видимости. Определить расстояние от точки D до плоскости треугольника ABC.

Данные для своего варианта взять из таблицы N2 по последней цифре кода.

Пример выполнения задачи приведён на рисунке 8.

Работу выполнять на листе формата А4.

Решение задачи следует начинать с анализа условий и возмож­ных путей решения.

Чтобы построить плоскость, перпендикулярную другой плоскости, надо провести её через перпендикуляр к этой плоскости. Кроме того, искомая плоскость должна содержать в себе и заданную прямую. Следовательно, первое, что потребуется выполнить - это пост­роить перпендикуляр к плоскости ABC, опущенный ив любой точки прямой DE (например из точки D). Плоскость, проходящая через пер­пендикуляр и прямую DE и будет искомой.

Перпендикуляр ив точки D к плоскости треугольника ABC можно провести используя горизонталь и фронталь, так как горизонтальная проекция, перпендикуляра перпендикулярна горизонтальной проекций горизонтали, а фронтальная проекция перпендикулярна фронтальной проекции фронтали.

Линию пересечения плоскости треугольника ABC и построенной перпендикулярной к ней можно построить, как в первой задаче, или любым другим способом.

Видимость плоскостей устанавливают с помощью конкурирующих точек скрещивающихся прямых, принадлежащих этим плоскостям.

Определить расстояние от точки D до плоскости треугольника ABC можно способом прямоугольного треугольника (на эпюре не пока­зано).

Таблица 2

№ вари-анта	Значения координат, мм
	xA	yA	zA	xB	yB	zB	xC	yC	zC	xD	yD	zD	xE	yE	zE
1	170	120	80	140	45	135	70	60	50	185	45	55	60	70	75
2	10	40	80	80	110	120	140	80	40	140	20	110	10	80	60
3	50	90	100	110	20	10	180	115	100	80	115	10	180	30	120
4	20	40	30	90	15	130	140	95	95	140	15	65	20	60	45
5	45	110	120	15	20	30	145	90	55	135	30	110	25	70	70
6	10	60	130	150	10	90	70	100	50	150	100	130	20	40	90
7	50	50	20	140	20	120	180	110	60	110	110	120	70	10	20
8	60	60	10	145	20	120	185	100	45	185	10	20	55	30	50
9	30	10	80	125	70	120	90	120	15	140	15	50	30	35	30
10	40	80	20	130	20	20	170	95	100	70	35	110	180	50	65

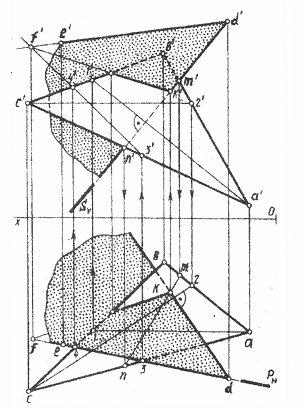
Рис. 2

Задача 3

Определить точки пересечения прямой линии с поверхностью пирамиды.

Данные для своего варианта ваять из таблицы 3. Пример выполнения задачи приведён на рисунке 3. Работу выполнять на листе формата А4.

Рекомендации по решению задачи

По координатам, взятым из таблицы для своего варианта, на эпюре обозначают проекции точек А, В, С, D, S и отроят проекции пирамиды SABCD. Затем строят проекции прямой линии МN.

Решение задачи выполняется в три этапа.

1. Через прямую MN проводят вспомогательную проецирующую плоскость Т.

2. Определяют проекции линии пересечения вспомогательной проецирующей плоскости с поверхностью пирамиды (в примере линия 1 2 3 4 1).

3. Находят точки пересечения проекции прямой MN с проекция­ми линий пересечения поверхности пирамиды и вспомогательной плос­кости.

В заключение определяют видимость прямой и видимые отрезки проводят сплошной основной линией, а невидимые - штриховой.

Задача может иметь одно из трёх решений: прямая пересекает поверхность пирамиды в двух точках, в одной точке (касается) или не пересекает поверхность.

Таблица 3 Данные к задаче 3 (размеры и координаты, мм)

№ вари-анта	xA	yA	zA	xB	yB	zB	xC	yC	zC	xD	yD	zD	xs	ys	zs	xM	yM	zM	xN	yN	zN
1	140	40	0	80	20	0	30	40	0	45	95	0	100	40	90	150	30	80	10	85	10
2	130	50	0	90	20	0	40	35	0	70	85	0	90	60	90	150	20	75	10	90	10
3	120	60	0	100	5	0	50	40	0	60	100	0	80	80	85	150	15	70	10	80	15
4	150	70	0	120	10	0	60	50	0	35	105	0	85	50	85	155	80	80	10	15	15
5	145	80	0	115	30	0	20	45	0	80	70	0	90	100	80	155	85	75	10	15	10
6	135	90	0	110	40	0	45	40	0	55	85	0	102	70	80	140	90	70	15	20	10
7	125	75	0	82	24	0	24	36	0	65	95	0	70	65	80	140	80	10	15	20	90
8	120	85	0	90	30	0	35	44	0	74	110	0	60	88	80	130	85	15	15	10	80
9	125	55	0	82	28	0	40	40	0	86	98	0	80	50	80	130	90	20	15	30	85
10	130	35	0	80	10	0	25	32	0	90	100	0	120	95	85	140	10	15	15	90	80
11	135	45	0	100	5	0	22	55	0	48	88	0	90	45	85	140	15	20	10	80	85
12	140	30	0	70	20	0	20	60	0	100	105	0	80	90	85	150	20	10	10	85	90
13	145	65	0	105	30	0	45	20	0	35	80	0	70	56	90	150	25	77	10	88	15
14	150	85	0	110	40	0	55	30	0	30	85	0	95	70	90	155	82	72	10	16	20
15	120	50	0	90	15	0	30	54	0	66	96	0	80	44	85	140	86	18	10	25	80
16	130	60	0	54	20	0	25	80	0	115	100	0	60	50	85	140	16	20	15	82	92
17	135	70	0	50	10	0	30	70	0	95	90	0	100	60	90	150	28	78	15	86	16
18	145	35	0	67	15	0	35	60	0	100	85	0	80	50	90	150	90	15	15	10	82

Рис.3