
- •Учебные карты. Часть 2
- •Введение
- •1. Таблица производных
- •2. Таблица интегралов
- •3. Методы интегрирования
- •4. Некоторые интегралы, содержащие квадратный трехчлен.
- •5. Интегралы от некоторых рациональных функций
- •6. Интегралы, содержащие тригонометрические и показательные функции
- •7. Несобственные интегралы
- •8. Функции нескольких переменных
- •10. Задачи о массе фигуры
- •16. Приложение интегралов по фигуре в механике
- •17. Скалярное поле (стационарное)
- •18. Векторное поле. Характеристики векторного поля
- •19. Дифференциальные уравнения первого порядка
- •20. Виды дифференциальных уравнений высших порядков, допускающих понижение порядка
- •21. Линейные однородные дифференциальные уравненияn-го порядка с постоянными коэффициентами
- •22. Линейные неоднородные дифференциальные уравненияn-го порядка с постоянными коэффициентами
- •23. Числовые ряды. Основные понятия
- •24. Числовые ряды с положительными членами
- •25. Знакопеременные числовые ряды
- •26. Функциональные ряды. Основные понятия
- •27. Степенные ряды
- •28. Разложение функции в степенной ряд
- •29 .Таблица разложений некоторых функций в степенные ряды
- •30. Разложение функции в тригонометрический ряд Фурье
17. Скалярное поле (стационарное)
|
Характеристики
скалярного поля, заданного функцией
| ||||
|
Понятие |
Определение и обозначение |
Геометрическая иллюстрация |
Вычисление | |
|
Скалярное поле |
Скалярным
полем называется часть пространства,
каждой точке
| |||
|
1. Линия, поверхность уровня |
Г.
м. т., в которых
|
плоскопараллельное поле |
эквипотенциальное поле |
Уравнение линии уровня:
Уравнение поверхности уровня
|
|
2. Производная по направлению
в
т.
|
|
|
В
частности, если
| |
|
3.
Градиент поля
в т.
|
|
|
В
частности, если
| |
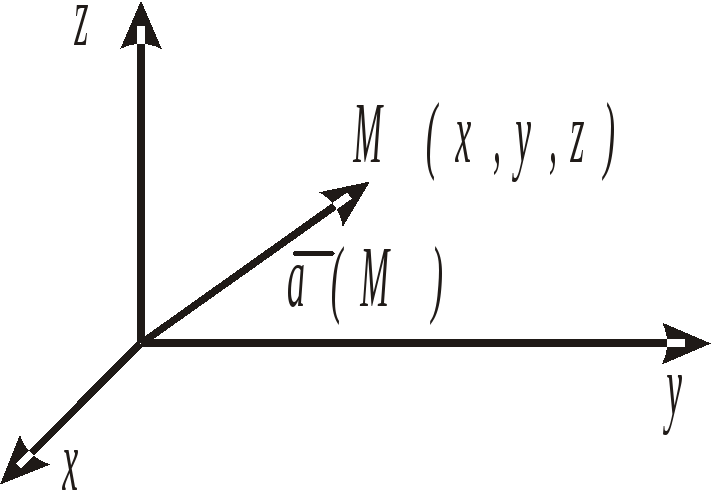
18. Векторное поле. Характеристики векторного поля
|
Понятие |
Определение и назначение |
Геометрическое изображение |
Вычисление |
|
1.Векторное поле
|
Каждой
точке
|
|
|
|
2.векторная
(силовая) линия поля
|
Линия,
во всякой точке которой вектор
|
|
Система дифференциальных уравнений, определяющая векторные линии |
|
3.Поток
поля
|
где
|
|
где
|
|
4. Дивергенция поля (расходимость поля) |
|
т.
|
Поле
|
|
5.
Поток поля
|
Формула Гаусса – Остроградского (связь между потоком и дивергенцией поля)
|
|
R:
|
|
6.
Ротор (вихрь) поля
|
|
|
Поле
потенциал
поля
|
|
7.
Работа поля
|
|
|
|
|
8.
Циркуляция поля
|
|
|
Вычисляется аналогично пункту 7. А=Ц, если Г – замкнутый контур. (В потенциальном поле Ц=0). |
|
9.
Циркуляция поля
|
Формула
Стокса устанавливает связь потока
вектора
|
|
|
|
10.Циркуляция
плоского поля
|
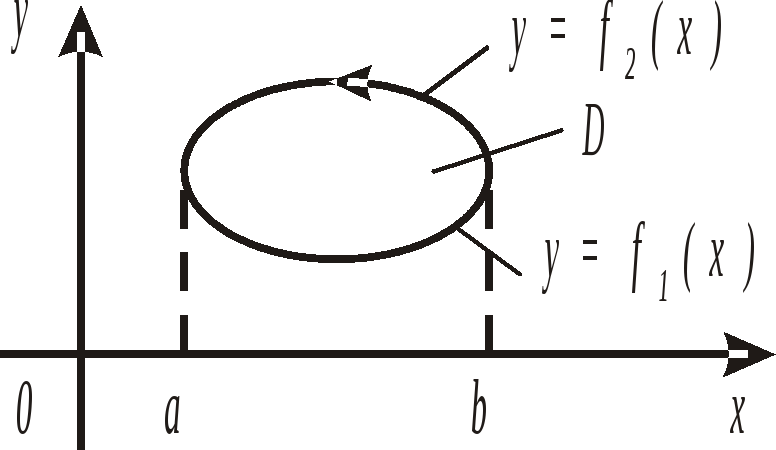
Формула Грина устанавливает связь вихря с циркуляцией плоского поля
|
|
|
19. Дифференциальные уравнения первого порядка
|
Тип уравнения |
Вид уравнения |
Признак типа уравнения |
Указания к решению уравнения |
|
1. Уравнение с разделяющимися переменными |
а)
б)
в)
|
а)
нет явно
б)
в)
|
а)
б)
в)
|
|
2. Однородное уравнение |
а)
б)
|
а)
б)
|
а)
б)
|
|
3. Уравнение в полных дифференциалах |
|
|
где
|
|
4. Линейное уравнение |
или
|
|
|
|
5. Уравнение Бернулли (линейное обобщенное) |
или
|
|
Решается тем же методом, что тип 4. |
Замечание.
Если удобнее рассматривать уравнение
не в виде
![]() ,
а в виде
,
а в виде![]() ,
где
,
где![]() ,
то всюду в указаниях к решению уравнения
,
то всюду в указаниях к решению уравнения![]() надо поменять местами
надо поменять местами![]() и
и![]() .
.











 -
-




 или
или
 ,
,