Математич действия над рез-тами измерений.

Часто неизвесные знач-я одних величин вычисляются на основании рез-тов других. Распространенной ошибкой при этом яв-ся обращение рез-тами как с неслучайными величинами.

Простейшим яв-ся вычисление по ф-ле , гдеfизвестная функция. Если А рез-т измерения, то это случайная величина подчиняется закону распределения, а данное преобразование связано с трансформацией этого закона.

Плотность распределения вероятности Qотражается через плотность распред-яи обратную ф-цию согласно теории вероятности след образом.

Например если рез-т измерения А – сторона квадрата и она подчиняется нормальному закону распределения вероятности

то плотность распред-я вероятности площади квадрата

;;

При сложных функциях fи законов распределения вероятности даже простейшие преобразования связаны со значительными математич трудностями. В этом случае ограничиваются приближенными вычислениями моментов, они основаны на разложении ф-ции в ряд в окресности точки. Этот способ становится фактически единственным, когда число переменных возрастает от 2-х и более.

Дисперсию рез-тов вычисления в этом случае можно записать как

Где и- сред квадратич отклонения рез-тов изм-я величины А и В.

R– смешанный центральный момент второго порядка совместного распределения случ величинxиy.

Величина называется корреляция.

Она служит мерой линейности статической связи между двумя случ. Величинами и указывает на то, как связаны между собой случайные величины xиyи как они обнаруживают тенденцию к синхронному изменению.

Например увеличение случайных значений величины xсопровождается нек-рым увеличением или уменьшением нек-рой величины у.

Обычно это происходит под влиянием фактора (например, изменением температуры). В этом случае корреляцию называют положительной.

Если значения принимаемых величин статически не связаны то R=0.

Такие величины назыв-ся некоррелированными.

На практике вместо второго центрального мом-та второго порядка может быть вычислена его

Оценка дисперсии в этом случае может быть представлена как

В этом случае рез-ты измерений должны сопровождаться указаними величин Q= ,S=,=,n=

Динамические измерения

Измерение Q(t)называется динамическим, если изменением измеряемой величины пренебречь нельзя.

При воздействии во времени на измерительный инструмент изменяющейся величины проявляются инерционные свойства измерительного прибора. Прибор не успевает реагировать на изменениеQ(t)в результате чего выходной сигнал оказывается искаженным.

Если выходной сигнал X(t)пересчитать на вход с помощью функции, обратной функции преобразования сигнала, то получим, что результат будет отличаться от входного воздействия на величину. Для определениянужно знать инерционные (динамические) свойства средства измерения. Эти свойства выражают с помощью динамических характеристик, которые однозначно устанавливают отклик средства измерения на входное воздействие.

Простейшим случаем входного воздействия является единичная ступень Q(t)=1(t). Отклик на такое воздействие называется переходная характеристика и обозначаетсяh(t). Она отражает переход от одного установившегося состояния на выходе к другому.

Если представить входной сигнал как суперпозицию простейших сигналов, то зная реакцию на простейшее воздействие можно определить реакцию измерительной системы на произвольное входное воздействие (справедливо в линейных измерительных системах, где суперпозиция входных воздействий соответствует суперпозиции выходных воздействий). Это позволяет сделать так называемый интеграл Дюамеля или интеграл наложения. О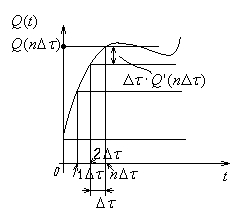тметки на каждую ступень смещены напропорционально величине этой ступени, тогда

. Устремляяк нулю получим одну из форм представления интеграла Дюамеля. . Интеграл Дюамеля имеет и другие формы записи:

(*)

Можно было бы предположить, что с помощью этих формул при известном h(t) решается основная задача измерения: определения входного воздействияQ(t) по отклику на негоX(t). Однако вследствие того, чтоX(t) иh(t) при измерениях с некоторой неопределенностью, решение этой задачи наталкивается на трудности.

На практике чаще всего ограничиваются оценками сверху и снизу. Для этого, учитывая априорную информацию оQ(t) выбирают модели входных воздействийи. При которыхибудут соответственно больше заданной. Затем с помощью одного из уравнения (*) при известной переходной характеристике вычисляютсяи. После по известной формулеопределяюти, позволяющий установить границы интервала неопределенности измеренияQ(t).

Другим видом испытательного сигнала простейшего входного воздействия является единичный импульс (функция Дирака):

.

Отклик системы на такое входное воздействие называется импульсной характеристикой . Для линейных систем справедливо. Используя это соотношение для интеграла Дюамеля можно записать:

Эти выражения при выборе соответствующих моделей позволяют с помощью импульсной характеристики установить пределы, в которых находится .иопределяются экспериментально.

При их использовании по методу суперпозиции осуществляется вначале разложение функции на элементарные функции времени, а затем суммируются отклики на них. Эту последнюю операцию называют свертыванием, а сами интегралы интегралами свертки. Спектр отклика средства измерения на единичный импульс называют комплексный коэффициент преобразования:

.

Изображение по Лапласу отклика средства измерения на единичный импульс называют передаточной функцией. Особенностью передаточной функции является возможность ее определения теоретическим путем, из дифференциального уравнения, описывающего зависимость выходной величины от входной.

Если динамическая характеристика определяется экспериментально, то ее выбор зависит от типов имеющихся приборов и видов входных воздействий, вполне возможно как временной так и частотный подход решения вопроса.

Динамические характеристики относятся к нормируемым метрологическим характеристикам средств измерения и должны поверяться.