9. Законы распределения вероятности:
Закон распределения вероятности результата измерения P(x) может относиться как к априорной, так и к апостариорной информации. В 1-ом случае он известен до измерения, во 2-ом – определяется экспериментально по результатам измерения. В обоих случаях этот закон характеризует неопределенность результата измерения. Он также отражает и нехватку знаний об измеряемой величине при определенных условиях.
1. Равномерный. Закон распределения непрерывной случайной величины называется равномерным, если на интервале, которому принадлежат все возможные значения случайной величины, плотность распределения сохраняет постоянное значение:
,
2. Треугольный (Симпсона).
?????
3. Нормальный (Гаусса). Непрерывная случайная величина называется распределенной по нормальному закону, если ее плотность распределения имеет вид:
,
Таким образом, нормальное распределение
определяется двумя параметрами:
иσ.
График плотности нормального распределения
называют нормальной кривой (кривой
Гаусса):
4. Нормированный
нормальный (стандартное нормальное
распределение).
Нормальное распределение с параметрами
,σ = 1
называется нормированным:
,
5. Распределение
Накагами:
,
где Г(·) – гамма-функция;x≥0,
параметры распределения: α>0 и β>0.
?
,
Г(·) – гамма-функция. Используется в
системах радиосвязи. Параметры
распределения: Ω - средняя мощность
замирающего сигнала,m
– глубина замираний.
6. Релея.
,
В – параметр.
7. Максвелла.
χ-распределение с n
степенями свободы:
.
При n=3
это выражение называется плотностью
распределения Максвелла и имеет вид:
.
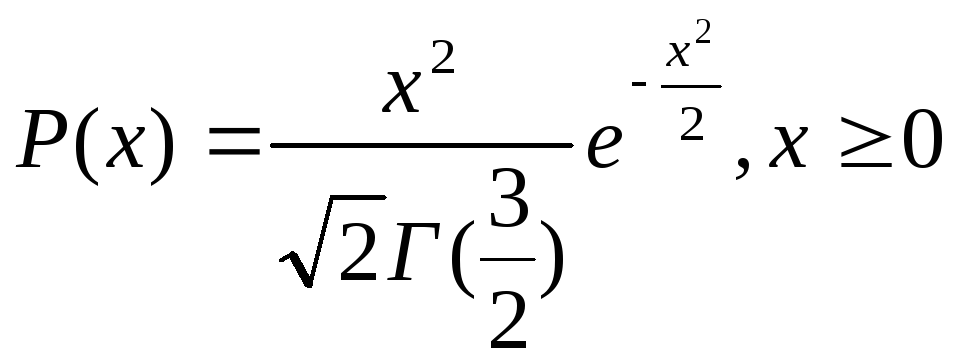8. χ-распределение модуля многомерного нормального вектора:
n-мерная непрерывная случайная величина имеет нормальное распределение, если ее многомерная плотность вероятности в матричном виде
9. Пирсона
(χ2-распределение)
с n
степенями свободы:
.
10. Стьюдента.
11. Фишера со степенями свободы m и n:
12. Коши
с параметрами:
13. Бета-распределение с параметрами α и β:
,
где
-
бета-функция.
14. Гамма-распределение (Эрланга) с параметрами α,λ>0:
,
где
.
15. Вейбула с параметрами α,λ>0:
16. Экспоненциальный односторонний (показательный) с параметром λ>0:
17. Экспоненциальный двусторонний (Лапласа) с параметрами аєR, λ>0^
18. Арксинуса:
