26. Корреляция как мера линейной статической связи между двумя случайными величинами.

Величина и называетсякорреляцией. Он служит мерой линейности статистической связи между двумя случайными величинами и указывает на то, как связаны между собой случайные величины x и yи как они обнаруживают тенденцию к синхронному изменению.

Напр., увеличение случайных значений величины x сопровождается и некоторым увеличение или уменьшением случайных значений y. Обычно это происходит под влиянием какого-то общего фактора, напр. изменения температуры. В этом случае корреляционный момент R>0, а корреляцию между случайными величинами x и yназывают положительной.

Если связь между случайными величинами подчиняется 2-му графику, то говорят, что R<0.

Если значения, принимаемые величинами, статистически не связаны, то их корреляционный момент R=0. Такие величины называются некоррелированными.

На практике вместо смешанного центрального момента 2-го порядка м.б. вычислена его оценка:

Оценка дисперсии м.б. представлена:

В этом случае результаты вычислений д. сопровождаться указаниями величин:

29. Динамические характеристики средств измерений.

Измерение Q(t) называется динамическим, если изменением измеряемой величины во времени пренебречь нельзя. Это, напр., измерение мгновенного значения переменного U-я и I. Измерение амплитуды, частоты, фазы того же переменного U-я или I к динамическим не относятся. При воздействии на СИ изменяющейся во времени физической величины начинают проявляться инерционный свойства СИ. Оно не успевает реагировать на изменение входного сигнала Q(t), в результате чего выходной сигнал оказывается искаженным по сравнению с входным.

Если выходной сигнал x(t) пересчитать на вход с помощью обратной функции преобразования сигнала, то результат будет отличаться от входного воздействия на какую-то величину ζ(t) – дзетта=Q(t)-x(t). Для определения ζ(t) нужно знать инерционные или динамические свойства СИ. Эти свойства выражаются с помощью динамических характеристик, которые однозначно устанавливают отклик СИ на входное воздействие.

31. Суммирование откликов (операция свертки). Интегралы свертки.

Отклик СИ на единичный импульс во временном представлении наз. импульсной хар-кой и обозн-ся как g(t). Поскольку единичный импульс является производной от единичной ступени, то отклик на единичный импульс на выходе линейного СИ (амплитудная хар-ка) является производной отклика на единичную ступень (переходная хар-ка): g(t)=h’(t). Используя это соотношение из интеграла Д м.записать:

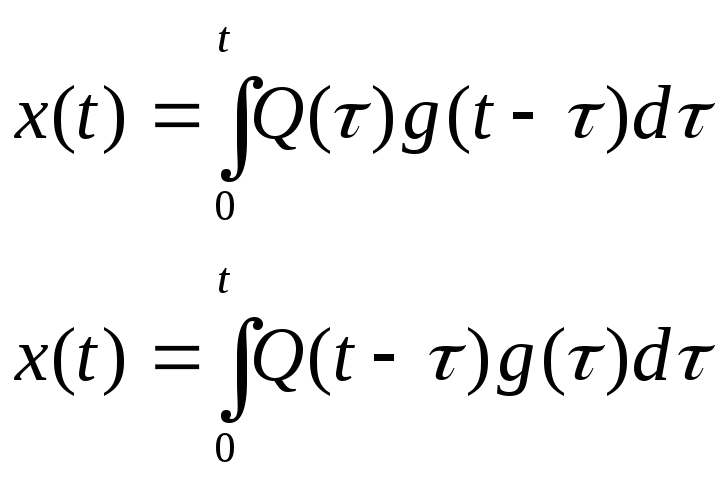
Эти выражения при выборе соответствующих моделей входных воздействий позволят с помощью импульсной хар-ки установить пределы, в которых находится ζ(t).

Переходная или импульсная хар-ки определяются экспериментально. При их использовании по м-ду суперпозиции осуществляется вначале разложение входной функции на элементарные функции времени, а затем суммируются отклики на них. Эту последнюю операцию называют свертыванием, а сами интегралы – интегралами свертки. Из них выбирается тот интеграл, у которого проще подынтегральная функция.