Вариант 21
.docx![]() ЗАДАНИЕ
N 1
отправить
сообщение разработчикам
Тема:
Элементы теории множеств
Даны
множества:
ЗАДАНИЕ
N 1
отправить
сообщение разработчикам
Тема:
Элементы теории множеств
Даны
множества:
![]() и
и
![]() Тогда
число элементов, принадлежащих их
пересечению равно …
Тогда
число элементов, принадлежащих их
пересечению равно …
|
|
|
3
|
![]() ЗАДАНИЕ
N 2
отправить
сообщение разработчикам
Тема:
Метрические пространства
Расстояние
между точками
ЗАДАНИЕ
N 2
отправить
сообщение разработчикам
Тема:
Метрические пространства
Расстояние
между точками
![]() и
и
![]() в
метрике
в
метрике
![]() ,
где
,
где
![]() и
и
![]() ,
равно …
,
равно …
|
|
|
|
10 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
– 1 |
![]() ЗАДАНИЕ
N 3
отправить
сообщение разработчикам
Тема:
Мера плоского множества
Мера
плоского множества, изображенного на
рисунке,
ЗАДАНИЕ
N 3
отправить
сообщение разработчикам
Тема:
Мера плоского множества
Мера
плоского множества, изображенного на
рисунке,
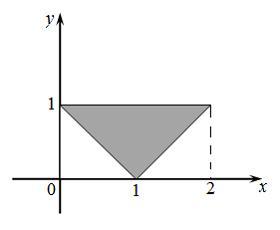 равна …
равна …
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]() ЗАДАНИЕ
N 4
отправить
сообщение разработчикам
Тема:
Отображение множеств
Образом
отрезка
ЗАДАНИЕ
N 4
отправить
сообщение разработчикам
Тема:
Отображение множеств
Образом
отрезка
![]() при
отображении y
=
2x
является …
при
отображении y
=
2x
является …
|
|
|
|
[0,5; 2] |
|
|
|
|
[– 2; 2] |
|
|
|
|
[– 0,5; 2] |
|
|
|
|
|
Решение:
Образом
множества
![]() при
отображении y
=
2x
являются те точки
при
отображении y
=
2x
являются те точки
![]() в
которые при данном отображении
попадают точки x
из
в
которые при данном отображении
попадают точки x
из
![]() В
нашем случае это множество
В
нашем случае это множество![]()
![]() ЗАДАНИЕ
N 5
отправить
сообщение разработчикам
Тема:
Приложения определенного интеграла
Площадь
фигуры, изображенной на рисунке
ЗАДАНИЕ
N 5
отправить
сообщение разработчикам
Тема:
Приложения определенного интеграла
Площадь
фигуры, изображенной на рисунке
 равна
…
равна
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]() ЗАДАНИЕ
N 6
отправить
сообщение разработчикам
Тема:
Дифференциальное исчисление ФНП
Значение
частной производной
ЗАДАНИЕ
N 6
отправить
сообщение разработчикам
Тема:
Дифференциальное исчисление ФНП
Значение
частной производной
![]() функции
функции
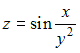 в
точке
в
точке
 равно …
равно …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]() ЗАДАНИЕ N 7
отправить
сообщение разработчикам
Тема:
Основные методы интегрирования
Множество
первообразных функции
ЗАДАНИЕ N 7
отправить
сообщение разработчикам
Тема:
Основные методы интегрирования
Множество
первообразных функции
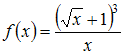 имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Чтобы
определить множество первообразных,
вычислим неопределенный интеграл от
этой функции. Тогда


![]() ЗАДАНИЕ
N 8
отправить
сообщение разработчикам
Тема:
Непрерывность функции, точки разрыва
Функция
ЗАДАНИЕ
N 8
отправить
сообщение разработчикам
Тема:
Непрерывность функции, точки разрыва
Функция
![]() непрерывна
на отрезке …
непрерывна
на отрезке …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Определим
точки разрыва данной дробно-рациональной
функции, приравняв к нулю знаменатель:
![]() Тогда
данная функция непрерывна при всех x,
кроме
Тогда
данная функция непрерывна при всех x,
кроме
![]() .
Тогда
.
Тогда
![]() будет
непрерывна, например, на отрезке
будет
непрерывна, например, на отрезке
![]() так
как
так
как
![]()
![]() ЗАДАНИЕ N 9
отправить
сообщение разработчикам
Тема:
Однородные дифференциальные уравнения
Общий
интеграл дифференциального уравнения
ЗАДАНИЕ N 9
отправить
сообщение разработчикам
Тема:
Однородные дифференциальные уравнения
Общий
интеграл дифференциального уравнения
![]() имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Запишем
уравнение в виде
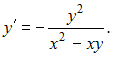 Сделаем
замену
Сделаем
замену
![]() Тогда
Тогда
![]()
![]() и
уравнение запишется в виде
и
уравнение запишется в виде
 Разделим
переменные:
Разделим
переменные:
![]() и
проинтегрируем обе части последнего
уравнения:
и
проинтегрируем обе части последнего
уравнения:
![]() Сделаем
обратную замену:
Сделаем
обратную замену:
![]()
![]() ЗАДАНИЕ
N 10
отправить
сообщение разработчикам
Тема:
Линейные дифференциальные уравнения
второго порядка с постоянными
коэффициентами
Общий
вид частного решения
ЗАДАНИЕ
N 10
отправить
сообщение разработчикам
Тема:
Линейные дифференциальные уравнения
второго порядка с постоянными
коэффициентами
Общий
вид частного решения
![]() линейного
неоднородного дифференциального
уравнения второго порядка
линейного
неоднородного дифференциального
уравнения второго порядка
![]() будет
выглядеть как …
будет
выглядеть как …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Общее
решение этого уравнения можно записать
в виде
![]() ,
где функция
,
где функция
![]() –
общее решение однородного уравнения
–
общее решение однородного уравнения
![]() а
функция
а
функция
![]() –
некоторое частное решение исходного
неоднородного уравнения.
Для однородного
уравнения составим характеристическое
уравнение
–
некоторое частное решение исходного
неоднородного уравнения.
Для однородного
уравнения составим характеристическое
уравнение
![]() и
найдем его корни:
и
найдем его корни:
![]() Тогда
общее решение однородного уравнения
будет иметь вид
Тогда
общее решение однородного уравнения
будет иметь вид
![]() Поскольку
правая часть исходного уравнения
Поскольку
правая часть исходного уравнения
![]() то
имеем уравнение
со специальной правой
частью. Так как
то
имеем уравнение
со специальной правой
частью. Так как
![]() не
является корнем характеристического
уравнения, а
не
является корнем характеристического
уравнения, а
![]() –
является, то частное решение
–
является, то частное решение
![]() неоднородного
уравнения будем искать в виде
неоднородного
уравнения будем искать в виде
![]()
![]() ЗАДАНИЕ
N 11
отправить
сообщение разработчикам
Тема:
Типы дифференциальных уравнений
Уравнение
ЗАДАНИЕ
N 11
отправить
сообщение разработчикам
Тема:
Типы дифференциальных уравнений
Уравнение
![]() является …
является …
|
|
|
|
линейным неоднородным дифференциальным уравнением первого порядка |
|
|
|
|
однородным относительно x и y дифференциальным уравнением первого порядка |
|
|
|
|
уравнением Бернулли |
|
|
|
|
дифференциальным уравнением с разделяющимися переменными |
![]() ЗАДАНИЕ
N 12
отправить
сообщение разработчикам
Тема:
Системы двух линейных дифференциальных
уравнений с постоянными коэффициентами
При
решении системы дифференциальных
уравнений
ЗАДАНИЕ
N 12
отправить
сообщение разработчикам
Тема:
Системы двух линейных дифференциальных
уравнений с постоянными коэффициентами
При
решении системы дифференциальных
уравнений
 можно
получить уравнение второго порядка
вида …
можно
получить уравнение второго порядка
вида …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]() ЗАДАНИЕ
N 13
отправить
сообщение разработчикам
Тема:
Интерполирование функций: интерполяционные
полиномы Лагранжа
Функция
ЗАДАНИЕ
N 13
отправить
сообщение разработчикам
Тема:
Интерполирование функций: интерполяционные
полиномы Лагранжа
Функция
![]() задана
таблично:
задана
таблично:
 В
интерполяционном полиноме Лагранжа
2-ой степени с узлами
В
интерполяционном полиноме Лагранжа
2-ой степени с узлами
![]() составленном
по этой таблице для приближенного
вычисления
составленном
по этой таблице для приближенного
вычисления
![]() при
условии
при
условии
![]() значение
значение
![]() не
может быть равно …
не
может быть равно …
|
|
|
|
12 |
|
|
|
|
6 |
|
|
|
|
5 |
|
|
|
|
8 |
Решение:
Для
получения интерполяционного полинома
Лагранжа 2-ой степени требуются три узла
![]() и
значения данной функции в них:
и
значения данной функции в них:
![]() Это
могут быть любые три точки
Это
могут быть любые три точки
![]() из
таблицы, удовлетворяющие двум условиям:
из
таблицы, удовлетворяющие двум условиям:
![]() и
и
![]() Следовательно,
в качестве узла
Следовательно,
в качестве узла
![]() нельзя
брать 6, 8, 10, 11. Значит,
нельзя
брать 6, 8, 10, 11. Значит,
![]() не
может принимать значения 12, 13, 20, 23.
не
может принимать значения 12, 13, 20, 23.
![]() ЗАДАНИЕ N 14
отправить
сообщение разработчикам
Тема:
Численные методы решения дифференциальных
уравнений и систем
Для
задачи Коши
ЗАДАНИЕ N 14
отправить
сообщение разработчикам
Тема:
Численные методы решения дифференциальных
уравнений и систем
Для
задачи Коши
![]() выполнен
один шаг получения приближенного решения
методом Эйлера - Коши с шагом
выполнен
один шаг получения приближенного решения
методом Эйлера - Коши с шагом
![]()
 Тогда
значение y1,
записанное с двумя знаками после запятой,
равно …
Тогда
значение y1,
записанное с двумя знаками после запятой,
равно …
|
|
|
|
1,12 |
|
|
|
|
0,9155 |
|
|
|
|
1,11 |
|
|
|
|
1,1155 |
Решение:
По
условию задачи известно, что начальная
точка интегральной кривой имеет
координаты:
![]() Правая
часть уравнения:
Правая
часть уравнения:
![]() Получим
следующую точку:
Получим
следующую точку:
![]()

![]() ЗАДАНИЕ
N 15
отправить
сообщение разработчикам
Тема:
Численное дифференцирование и
интегрирование
Значение
дифференцируемой функции z = f (x,
y)
в точке
ЗАДАНИЕ
N 15
отправить
сообщение разработчикам
Тема:
Численное дифференцирование и
интегрирование
Значение
дифференцируемой функции z = f (x,
y)
в точке
![]() можно
приближенно найти как …
можно
приближенно найти как …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Воспользуемся
приближенной формулой
![]() В
нашем случае
В
нашем случае
![]()
![]()
![]()
![]()
![]()
![]() Тогда
Тогда
![]() .
.
![]() ЗАДАНИЕ N 16
отправить
сообщение разработчикам
Тема:
Ряд Фурье. Теорема Дирихле
Значение
ряда Фурье функции
ЗАДАНИЕ N 16
отправить
сообщение разработчикам
Тема:
Ряд Фурье. Теорема Дирихле
Значение
ряда Фурье функции
![]() в
точке
в
точке
![]() равно …
равно …
|
|
|
|
0 |
|
|
|
|
– 1 |
|
|
|
|
1 |
|
|
|
|
|
Решение:
Значение
ряда Фурье на границах отрезка задания
![]() вычисляется
по формуле
вычисляется
по формуле
![]() тогда
тогда
![]()
![]() ЗАДАНИЕ N 17
отправить
сообщение разработчикам
Тема:
Гармонические колебания
Точка
совершает гармонические колебания
вдоль оси Ox
с амплитудой
ЗАДАНИЕ N 17
отправить
сообщение разработчикам
Тема:
Гармонические колебания
Точка
совершает гармонические колебания
вдоль оси Ox
с амплитудой
![]() Тогда
уравнение этих колебаний может иметь
вид …
Тогда
уравнение этих колебаний может иметь
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|