Теорема 15.5.1

Если ф-я y=f(x) во всех точках (a;b) имеет отрицательную вторую производную т.е. f ^II <0, то график ф-ии на этом интервале выпуклый вверх. Если f ^II >0, то он выпуклый вниз.

Достаточное условие существования точек перегиба.

Если f ^II(x) при переходе через x₀ в которой она равна 0 или не существует, меняет знак то точка графика с абсциссой x₀ есть точка перегиба.

ПРИМЕР:

y=x⁵-x+5

y^I=5x ⁴-1

y^II=20x³

20x³=0

x=0

Г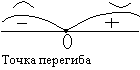рафик выпуклый вверх в интервале (-;0), график вогнутый на (0; +), (0;5) – точка перегиба.

№67 Асимптоты графика функции.

Прямая l наз-ся асимптотой кривой y=f(x), если при удалении точки М(х;у) по кривой в бесконечность расстояние от точки М(х;у) стремится к 0.

Если асимптота параллельна Oy , то она называется вертикальной.

Если асимптота образует с O_x угол не равный 90⁰, то она наз-ся наклонной.

Lim f(x)=

xa

x=a –есть уравнение вертикальной асимптоты.

Для отыскания вертикальной асимптоты нужно найти х вблизи которого функция f(x) возрастает по модулю. Обычно это точки разрыва второго рода. Уравнение наклонной асимптоты будем искать в виде y=kx+b, где

k=Lim f(x)/x

x

b=Lim (f(x)-k(x))

x

Если хотя бы один из этих пределов не существует, то кривая асимптоты не имеет. Если k=0,bимеет конечное значение, то асимптота наз-ся горизонтальной.

№68 Функции двух переменных. Предел функции.

Переменная Z называется функцией 2-х переменных x и y, если каждой паре значений x и y из области их изменения соответствует определенное значение Z. Переменные x и y в этом случае называются независимыми переменными или аргументами.

Обозначение

Z= Z(x;y)

F=f(x;y)

Если x=a, y=b, то Z=f(a;b) называют частными значениями функции Z при x=a, y=b. Если x,y,z считать прямоугольными координатами точки M(x;y;z), то каждая пара значений аргументов (x;y) определяет на плоскости _xO_y некоторую точку P(x;y), а Z в точке (x;y) есть аппликата точки М.

Областью определения функции Z=f(x;y) называется совокупность всех, тех точек плоскости _xO_y в которых Z принимает действительные значения для данной функции Z=f(x;y). Областью существования может служить или вся плоскость _xO_y, или некоторая ее часть ограниченная одной или несколькими непрерывными линиями, которые называются границами области. Область называется замкнутой если она содержит все точки границы области.

Способы задания:

• табличный

• графический

• аналитический

Частное и полное приращение функции 2-х переменных.

Z=f(x;y)

Если переменной х дадим приращение ∆x , оставляя ри этом переменную y неизменной, то f(x+∆x;y)-f(x;y) называется частным приращением Z по переменной x. Обозначение:

1. ∆_xZ=f(x+∆x ; y) – f(x;y)

2. ∆_yZ=f(x ; y+∆y) – f(x;y)

3. ∆Z=f(x+∆x ; y+∆y) – f(x;y) – полное приращение функции Z.

Предел функции 2-х переменных.

Множество всех точек М(х;у) координаты которых удовлетворяют неравенству:

называются δ-окрестностью точки М₀(х₀;у₀), т.е. δ-окрестность точки М₀ – это все внутренние точки круга с центром М₀ и радиусом R= δ.

Пусть функция Z=f(x;y) определена в некоторой окрестности точки М₀(х₀;у₀) , кроме быть может самой этой точки. Число А называется пределом ф-ии Z=f(x;y) при х→х₀ , у→у₀ если при любом E>0 существует δ>0, такое, что при любом х≠х₀ и у≠у₀ и удовлетворяет неравенству :

выполняется неравенство |f(x ; y-A)|<E

Запись:

A=lim f(x;y)

x→x₀

y→y₀

Lim f(M)

M→M0

№69 Непрерывность функции 2-х переменных.

Функция Z=f(x;y) называется непрерывной в точке М₀(х₀;у₀) если она:

• определена в этой точке и некоторой ее окрестности

• Имеет lim f(M)

M→M₀

• Этот предел равен значению функции Z в точке М₀

Функция непрерывная в каждой точке некоторой области называется непрерывной в этой области. Точки в которых не выполняется хотя бы одно из условий называются точками разрыва. Точки разрыва могут образовывать линии разрыва.

ПРИМЕР:

Z= 2/y-x

y=x– линия разрыва.

№70 Частные производные первого порядка, их геометрический смысл.

Пусть Z=f(x;y) непрерывна в некоторой области, как было отмечено ранее если х получает приращение ∆х , а у сохраняет свое значение то функция Z получает частное приращение ∆_xZ. Частной производной по х от Z=f(x;y) называется .

Таким образом частная производная функций нескольких переменных определяется как производная функции одной из этих переменных, при условии постоянства значений остальных независимых переменных.

№71 Частные производные высших порядков.

и - частные производные 1-го порядка. Их можно рассматривать как функции от (x;y) принадл. D. Они могут иметь частные производные, которые называются частными производными второго порядка.

Частная производная 2-го или более высшего порядка взятая по различным переменным называется смешанной частной производной.

ПРИМЕР:

Z=x⁴-2x²y³+y⁵+1

72. Полный дифференциал функции.

Определение. Функция z = (x, у) называется дифференци­руемой в точке Р (х, у), если ее полное приращение z можно пред­ставить в следуюирм виде:

z = Az + By + (x; y), где x и y - любые приращения соответствующих аргументов х и у в некоторой окрестности точки Р; А и В — постоянные (т. е, величины, не зависящие от x и y); (x, у) - бесконечно малая более высокого порядка, чем расстояние  = Sqr(x^2 + y^2) между точками Р (х; у) и P1(x+ x; у + у) (т. е. lim((((x, y))/()) = 0).

Таким образом, если функция z = f(x, у) дифференцируема в данной точке, то согласно формуле, ее полное приращение в этой точке состоит из двух частей: главной части приращения Ах + By, линейной относительно x и y, и нелинейной части (x, y), более высокого порядка малости, чем главная часть приращения.

Определение. Главная часть приращения функции z = f(x, у), линейная относительно x и y, называется полным дифференциа­лом этой функции и обозначается символом dz или df(x, у). Таким образом, dz = Ax + By.

В выражении для дифференциала Ax + By величины А и В не зависят от x и y, но зависят от точки Р (х, у), в которой этот дифференциал рассматривается. Иными словами, А и В, яв­ляются функциями х и у.

73. Необходимые и достаточные условия дифференцируемости функции.

Т1. Достаточное условие дифференцируемости функции.

Если функция Z = f(x, y) имеет непрерывные частные производные Z’x и Z’y в точке с координатами (x, y), то она дифференцируема в этой точке и ее полный дифференциал выражается:

dZ = ((dZ)/(dx))dx + ((dZ)/(dy))dy

Т2. Необходимые условия дифференцируемости функции.

Если функция Z = f(x, y) – дифференцируема в точке M с координатами (x, y), то она непрерывна в этой точке, то она имеет частные производные.

74. Приминение полного дифферинциала к приближенным вычислениям.

Полным дифференциалом функции нескольких переменных можно пользоваться для приближенных вычислений. Пусть дана дифференцируемая функция z = f(x, у). Ее полное приращение выражается формулой:

z = f’x(x, y)x + f’y(x, y)y + (x, y)

Здесь (x, y) стремится к нулю быстрее, чем  = Sqr((x^2) + (y^2)). Поэтому при малых , т. е. при малых |x| и |y|, слагаемым (x, y) можно пренебречь и писать:

z  f’x(x, y)x + f’y(x, y)y (21)

т. е. приращение функции приближенно можно заменить ее пол­ным дифференциалом. Так как z = f(x, y), то:

z = f(x + x, y + y) – f(x, y)

Представляя это выражение для z в формулу (21), получим:

f(x + x, y + y) – f(x, y)  f’x(x, y)x + f’y(x, y)y, откуда:

f(x + x, y + y)  f(x, y) + f’x(x, y)x + f’y(x, y)y (22)

Формулой (22) можно пользоваться для приближенных вычис­лений значений функции двух переменных в точке Р(x + x, y + y), близкой к точке Р(x, y), если известны значения функции и ее частных производных в самой точке Р(х; у).

75. Дифференцирование сложной функции. Полная производная.

Пусть Z = f(x; y) – функция двух независимых переменных, каждая из которых является функцией независимой переменной t, т. е. x = f1(t) и y = f2(t), тогда Z = f(f1(t); f2(t)) – есть сложная функция от независимой переменной t.

Если функции f1(t) и f2(t) – дифференцируемы в точку t, а функция Z = f(x; y) – дифференцируема в точке (x; y), то сложная функция Z = f(f1(t); f2(t)) – дифференцируема в точке t, и ее производная: (dZ)/(dt) = ((dZ)/(dx)) * ((dx)/(dt)) * ((dZ)/(dy)) * ((dy)/(dt)).

76. Дифференцирование неявной функции.

Как известно, неявная функция у, аргумента х задается урав­нением F(x; y) = 0, не разрешенным относительно у.

Мы знаем, что не всякое уравнение, связывающее х и у, опре­деляет неявную функцию. Например, уравнение x^2 + y^2 + 1 = 0 не определяет функции у.

Каким же условиям должно удовлетворять уравнение F(x, y) =0, чтобы оно определяло неявную функцию у.

77. Необходимые и достаточные условия экстремала.

Пусть P0 (x0; y0) – стационарная точка функции Z = f(x; y), имеющей непрерывные частные производные 1 и 2 порядка в этой точке. Значение производной 2 порядка P0 обозначим: ((d^2 Z)/(dx^2)) = A; ((d^2 Z)/(dx^2 dy^2)) = B; ((d^2 Z)/(dy^2)) = C

a = AC – B^2

Если a < 0, то в стационарной точке экстремума нет.

Если а > 0, то экстремум есть, причем максимум.

Если а = 0, то требуется дополнительное исследование.

78. Наибольшее и наименьшее значения функции в заданной замкнутой области.

Пусть требуется найти минимум и максимум функции Z = f(x; y), в некоторой замкнутой области D. Этих значений функция достигает либо на внутренних точках области, либо на границе области.

Чтобы найти минимум и максимум функции в заданной замкнутой области, необходимо:

1. Найти стационарные точки, лежащие внутри области и вычислить значение функции в этих точках, исследовать их на экстремумы не обязательно.

2. Найти наибольшее и наименьшее значение функции на границе области. Если граница состоит из нескольких участков, то исследование проводится для каждого отдельно.

3. Сравнить все полученные значения функции, наибольшее будет максимумом, а наименьшее – минимумом, в заданной замкнутой области.