Вопрос 11.

Свойства ф-ции.

Область существования и область значения ф-ции.

Определение: областью существования (или областью определения) ф-ции y=f(x) называется савокупность всех действительных значений аргумента x, для которых ф-ция y определена, т. е. существует и выражается действительным числом.

Совокупность всех значений, которые принимает при этом сама ф-ция y называется областью значений (или областью изменений).

Чётность и нечётность.

Определение: ф-ция y=f(x) называется чётной, если для всех x из области определения

f(-x)=f(x). График чётной ф-ции симметричен относительно оси Oy.

Определение: ф-ция y=f(x) называется нечётной, если для всех x из области определения

f(-x)=-f(x). График чётной ф-ции симметричен относительно начала координат.

Если ни одно из вышеуказанных условий не выполняется, т. е. f(-x)f(x) и f(-x)-f(x), то ф-ция y=f(x) называется ф-цией общего вида.

Периодичность.

Определение: ф-ция y=f(x) называется периодической с периодом T0, если для любых x из области определения справедливо равенство f(x+T) = f(x).

Примечание: если число T есть период ф-ции y=f(x) заданной на всей числовой прямой, то число nT, nZ также является периодом ф-ции. В этом случае наименьший положительный период, если он существует, называется основным периодом ф-ции.

Говоря о периоде ф-ции обычно имеют в виду наименьший положительный период.

Монотонность.

Определение: ф-ция y=f(x) называется возрастающей на некотором интервале, если на этом интервале большему значению x соответствует большее значение ф-ции, т. е. при x₁<x₂ имеет место неравенство f(x₁)<f(x₂).

Определение: ф-ция y=f(x) называется убывающей на некотором интервале, если на этом интервале большему значению x соответствует меньшее значение ф-ции, т. е. при x₁<x₂ имеет место неравенство f(x₁)>f(x₂).

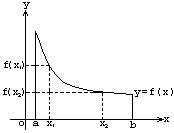
Ф-ции возрастающие и убывающие называются монотонными ф-циями.

Ф-ция y=f(x) называется кусочно-монотонная, на некотором интервале, если его можно разбить на конечное число интервалов так, что на каждом из них ф-ция изменяется монотонно, т. е. или возрастает или убывает.

Ограниченность.

Ф-ция y=f(x) называется ограниченной на некотором промежутке, или существует такое положительное число M>0, что |f(x)|M, для любого xX.

Если ф-ция ограничена на некотором промежутке, то график этой ф-ции в пределах этого интервала расположен в полосе ограниченной прямыми y=a и y=b.

Вопрос 12.

Обратная функция и её график.

Пусть y=f(x) есть ф-ция от независимой переменной x, определённой на множестве X с областью значения Y. Поставим в соответствии каждому значению yY единственное значение xX при котором f(x)=y. Тогда полученная ф-ция x=(y)=f^-1(y) определённая на множестве Y с областью значений X называется обратной.

Чтобы найти ф-цию x=(y) обратную ф-ции y=f(x) достаточно решить уравнение f(x)=y относительно x (если это возможно).

Если сохранить обычные обозначения, т. е. если во всех случаях x считать аргументом, а y – ф-цией, то получим, что y=(x) является обратной функции y=f(x). График обратной ф-ции y=(x) симметричен относительно прямой y=x.

Из определения обратной ф-ции вытекает, что ф-ция y=f(x) имеет обратную т. т. т. когда ф-ция y=f(x) задаёт взаимооднозначное соответствие между множествами X и Y. Отсюда следует, что любая строго-монотонная ф-ция имеет обратную. При этом если ф-ция возрастает (убывает), то обратная ф-ция такжк возрастает (убывает).