5.3. Касательные напряжения и проверка прочности балок по касательным напряжениям

В произвольной точке прямоугольного поперечного сечения балки (рис. 3.6) касательное напряжение определяют по формуле Д. И. Журавского:

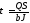(3.10)

где Q — поперечная сила в рассматриваемом сечении; статический момент относительно нейтральной осиz части площади сечения,

рис. 5. лежащей по одну сторону от уровня у, на котором опре­деляется напряжение; b—ширина сечения и J = bh³/12—момент инерции площади сечения относительно оси x.

Наибольшие касательные напряжения по­лучаются в точках нейтральной оси (у=0). Они имеют значение

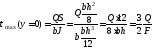(3.11)

где F=bh—площадь поперечного сечения балки.

По формуле (3.10) приближенно можно подсчитывать состав­ляющие касательных напряжений, перпендикулярные нейтральной оси, для балок непрямоугольного сечения, понимая под b ширину сечения на уровне рассматриваемой точки. Результирующие каса­тельные напряжения в точках контура сечения направлены по касательным к контуру сечения, а в других точках сечения они как-то наклонены к плоскости действия сил.

Точно найти касательные напряжений в балках произвольной формы сечения весьма сложно. Приближенное их определение ос­новано на некоторых произвольных допущениях о направлении касательных напряжений внутри сечения.

Прочность балки по касательным напряжениям проверяется в точках с максимальными касательными напряжениями того попе­речного сечения, в котором действует наибольшая по абсолютному значению поперечная сила Q_max.

Проверке следует подвергать короткие балки, балки с тонкой и высокой стенкой сечения, балки, изготовленные из материала, плохо сопротивляющего­ся сдвигу и балки, не­сущие

большие нагрузки вблизи опор. Провероч­ная формула имеет вид

где S_Q—статический мо­мент относительно нейт­ральной оси части попе­речного сечения, лежа­щей по одну сторону ли­нии действия т_тах; b_о— ширина сечения на ли­нии действия т_тах. Для большинства проверяемых сечений т_тах действует в точ­ках нейтральной оси.

Допускаемое касательное напряжение обычно берут равным0,5—0,7 от []. Например, для СтОС и Ст2= 90МПа, для Ст3= 100 МПа, для сосны и ели=2МПа.

Пример: Дано: М₁ = 40 кНм, М₂ = 20 кНм, М₃ = 10 кНм, а=1 м; 6 = 4 cm; h =12 см (рис. 6). Определить а_А и х_л в сечении

Решение. Реакции опор

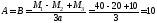кН.

Эпюры Q и М показаны на рис. 3.11. В сечении тп

М=- (30 + 20)/2 = - 25 кН-м; Q = 10 кН.

Так как точка А находится в растянутой зоне сечения, то по формуле (3.3) находим

Рис 6

Для прямоугольного сечения

Для рассматриваемой точки А

поэтому

Па = 130 МПа.

По формуле (3.10),

5.4. Главные напряжения и полная проверка прочности балок

В произвольной точке поперечного сечения балки, находящейся на расстоянии у от нейтральной оси г, нормальные и касатель­ные напряжения определяют по формулам

, момент инерции и статический момент относительно нейтральной оси х

Эле­мент, выделенный около этой точки бесконечно близкими попереч­ными сечениями на расстоянии dх друг от друга и бесконечно близкими продольными сечениями, параллельными нейтральному слою, на расстоянии dу друг от друга, испытывает плоское на­пряженное состояние вида, указанного на рис. 3.14.

Нормальные 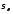и касательные напряжения в наклонной плоскости сечения,проходящей через эту точку (рис. 3.15), имеют значения

Две взаимно перпендикулярные наклонные плоскости являются главными плоскостями напряжений в данной точке балки, когда

. (3.14)

Главные напряжения а_£ и а₃ находят из выражения

Рис 9

Экстремальные касательные напряжения определяют по формуле

Графическое определение значений и направлений главных напряжений для четырех возможных вариантов напряженных со­стояний элементов, выделенных из балки, показано на рис. 3.16, а-г. Если в одном и том же поперечном сечении балки одновременно действуют максимальный изгибающий момент и макси­мальная поперечная сила или величины М и Q, близкие к макси­мальным, то в этом сече­нии производят проверку прочности балки по главным напряжениям.

Прочность по главным нап­ряжениям проверяют только для балок, поперечное сече­ние которых имеет тонкую стенку, резко расширяющую­ся вблизи крайних волокон. Проверку прочности произ­водят в точках перехода от малой ширины сечения к боль­шой. Балки из пластичного ма­териала проверяют по третьей гипотезе прочности по фор­муле

Балки из хрупкого материала проверяют по первой гипотезе прочности согласно условию

Полный расчет на прочность статически определяемой балки дадим в примере

Пример Дано: Р = 40 кН, q = 30 кН/м, а = 0,8 м, l = 4м, = 160МПа,= 100МПа (рис. 3.17). Определитьномер двутавровой балки.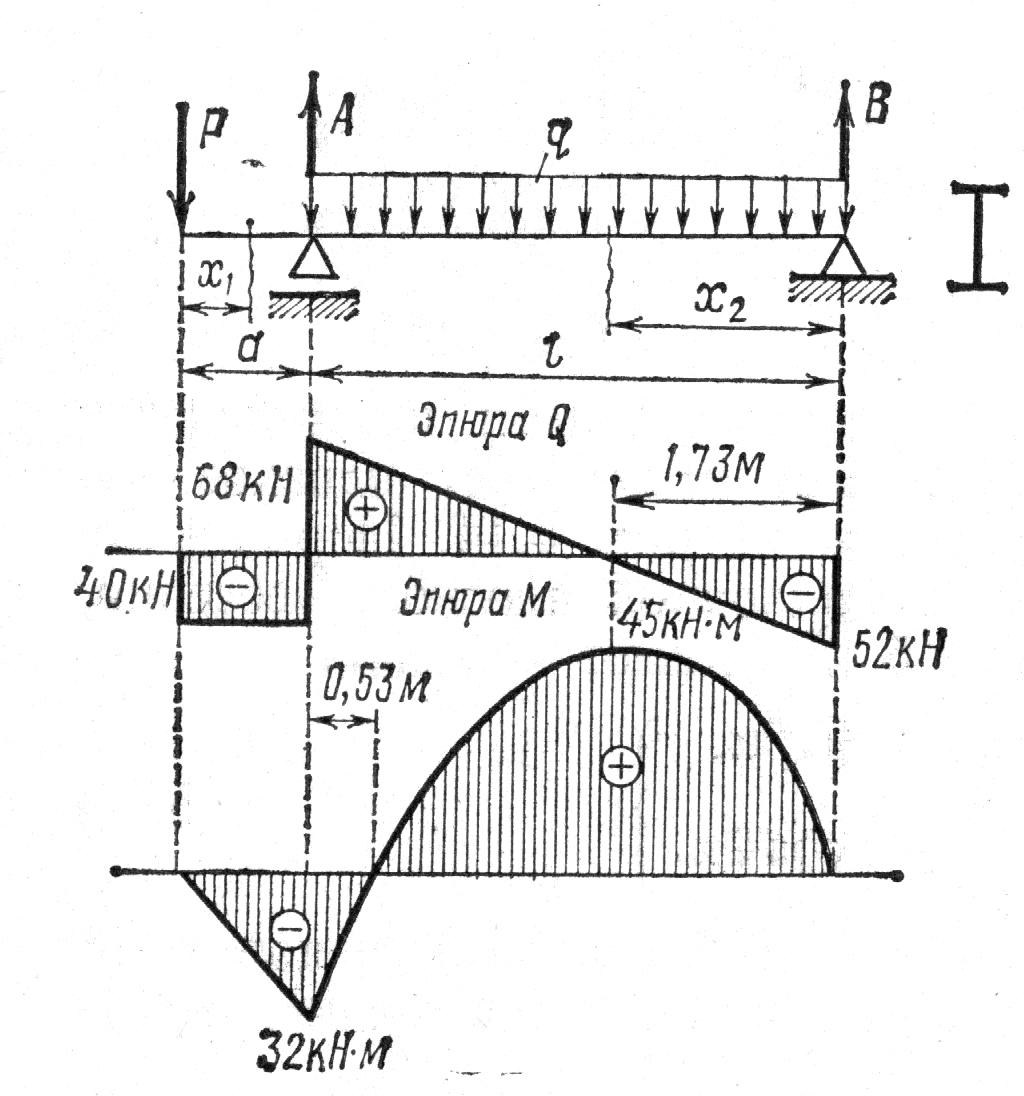

Решение. 1. Определение опорных реакций:

2. Построение эпюр Q и М. На консоли

В пролете между опорами

Так как Q_x2=- 52 + 30x₂ = 0 при x₂ = 52/₃₀= 1.73м, то

;

По этим данным на рис. 3.17 построены эпюры Q и М.

3. Подбор сечения двутавровой балки. Так как М_тах = 45кН-м, то. По сортаменту для двутавра № 22а W = 254 см³

(пере напряжение)

Для двутавра № 24 W= 289 см³,

(недонапряжение).

Выбираем двутавр № 24, для которого W = 289 см³,J = 3460 см⁴, S₀=163cm³, h = 24 см, b= 11,5см, t = — 0.95 см d = b₀ = 0 56 см. h₀ =h -2t =22,1 см (рис. 3.18). Этот двутавр будет работать при максимальном нормальном напряжении в крайнем волокне опасного сечения

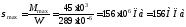
4. Проверка сечения балки по касатель­ным напряжениям. Так как Q_mах = 68кН,то

5. Построение эпюр нормальных касательных главных 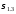и экстремальных касательных напряжений в неблагоприятном сечении балки и определение их направлений.

В отношении главных напряжений неблагоприятным является сечение над левой опорой (при подходе к ней справа), в котором М= —32кН*м и Q = 68kH

Нормальное напряжение в произвольной точке, находящейся на расстоянии у от нейтральной оси,

(а)

Статический момент площади полки относительно оси

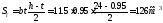
Статический момент части площади стенки по одну сторону от ординаты

Статический момент части сечения по одну сторону ординаты

Касательные напряжения для точек полки, согласно формуле (3.10),

(б)

а для точек стенки

= QS/(bJ). (в)

По формулам (а), (б), (в), (3.14), (3.15), (3.16) вычислены зна­чения- ,,, для у, отвечающего девяти точкам сечения. Полученные значения сведены в следующую таблицу:

Номер точек	У см						tg 2a
		МПа
1	12,00	111	0	±55,5	111	0	—0,00		0°0'		90°0'
2	11,05	102	2	±51	102	0	—0,0392		—1°7'		88°53'
3	11,05	102	44	±67	118	-16	—0,863		—20°24'		69°36'
4	5,52	51	53	±59	84	-34	—2,08		—32° 10'		57°50'
5	0,00	0	56	±56	56	-56	00		45°0'		45°0'
6	—5,52	—51	53	±59	34	-84	2,08		32°10'		122°10'
7	— 11,05	— 102	44	±67	16	-118	0,863		20°24'		110°24'
8	—11,05	—102	2	±51	0	-102	0,0392		1°7'		91°7'
9	—12,00	— 111	0	±55,5	0	-111	0,00		0°0'		90°0'

Эпюры напряжений изображены на рис. 5.19. Направления главных напряжений в рассмотренных точках сечения показаны на рис. 5.20. На рис..21 произведено графическое определение значений и направлений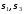в точках4,5,6.

5.5. Проверка прочности балки по главным напряжениям.

Наи­более опасной точкой в неблагоприятном сечении является точка 3. В этой точке =118 МПа и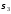— -16 МПа. Проверяем прочно­сть в этой точке по третьей гипотезе прочности согласно нера­венству . Так как118+ 16= 134 < 160, то выбранное се­чение прочно и по главным напря­жениям.

Рис. 136. Проверка прочности балки по главным напряжениям.

значений и направлений главных напряжений G_t и a₃ в точ­ках 4, 5 и 5.