Уравнение Шредингераа
Уравнение движения свободной частицычастицы
Волновая функция свободно движущейся частицы с энергией E
( r , t) (2 ) 3 / 2 ei(kr t) (2 ) 3 / 2 e i ( pr Et)
Дифференциальные уравнения, описывающие свободное движение частиц с энергией E
i |
d |
|
|
2 |
|
(*) |
|
|
|
||||
dt |
|
|
||||
|
|
2m |
|
|||
В том, что уравнение (*) справедливо, можно убедиться, вычислив временные и пространственные производные
|
|
|
|
|
|
|
|
d |
|
i |
E |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
2 |
|
2 |
|
2 |
|
dt |
|
|
|
|
|||||||||||||
|
|
|
|
|
1 |
|
( p x2 p 2y p z2 ) |
||||||||||||||||
x 2 |
y 2 |
|
z 2 |
|
|
2 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
p x2 p 2y |
p z2 |
E |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 m |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
d |
|
|
i |
|
|
|
2 |
|
2 |
|
2 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
d t |
2 m |
x 2 |
y 2 |
z 2 |
||||||||||||||||
Уравнение (*) является дифференциальным уравнением первого порядка по времени. Поэтому для определения волновой функции в произвольный момент времени t достаточно знать волновую функцию в начальный момент времени.
Уравнение Шредингера
i |
( r , t ) |
ˆ |
( r , t ) |
||
|
t |
|
H |
||
|
|
ˆ 2 |
|
|
|
|
ˆ |
|
p |
|
|
|
H |
|
2 m |
U ( r , t ) |
|
Эволюция квантовой системы в нерелятивистском случае описывается волновой функцией, удовлетворяющей уравнению Шредингера
i |
|
ˆ |
|
t |
H |
|
ˆ ( r , t ) — волновая функция,
H — оператор Гамильтона (оператор полной энергии системы).
Нобелевская премия по физике 1933 г. – Э. Шреденгер, П. Дирак.
За открытие новых плодотворных формулировок атомной теории
Почему уравнение Шредингера содержит мнимую единицу i?
Классические волны удовлетворяют классическому волновому уравнению
2 y 1 2 y .
x2 v2 t2
Среди классических волн важное место занимают гармонические волны с амплитудой y0 , частотой и периодом T .
|
|
|
|
|
|
x |
|
|
|
t |
|
|
2 |
|
||
y y0 |
cos(kx t) y0 cos 2 |
|
|
|
|
|
|
|
|
y0 |
cos |
|
(x vt), |
|||
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
T |
|
|
|
||||||
|
2 |
2 |
, |
k |
|
2 |
, |
|
v . |
|
||||||
|
T |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Уравнение Шредингера является уравнением первого порядка по времени и содержит множитель i .
i 2 U
t 2m
То, что уравнение Шредингера содержит первую производную по времени связано с квантовомеханическим принципом причинности. Если бы уравнение Шредингера содержало вторую производную по времени, то для определения волновой функции в любой произвольный момент времени было бы необходимо задание не только значения волновой функции в начальный момент времени, но и задание первой производной волновой функции во времени. Результаты измерений всегда должны быть представлены действительным числом, но волновая функция(x,t) не всегда является действительным числом, а может быть комплексной величиной. Например, волновая
функция свободной частицы имеет вид (x,t) Aei(kx t ) .
Поэтому волновая функция (x,t) не является непосредственно наблюдаемой величиной, в отличие от классической
волны. Однако наблюдаемой величиной является вероятность того или иного события, которая определяется квадратом модуля волновой функции
W (x,t) 2 * (x,t) (x,t).
Стационарное уравнение Шредингераингера
Если гамильтониан системы не зависит от времени, стационарное уравнение Шредингера имеет вид
|
2 |
d 2 |
U ( x) E ( x) |
|
2m dx2 |
||||
|
|
|||
Величина Е имеет смысл собственного значения энергии системы, а Ψ(x) описывает состояние с заданной энергией.
Оператор Гамильтона может иметь как дискретный так и непрерывный спектр энергий.
2m (E U ) 0
2
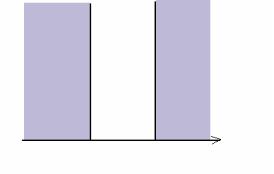
Бесконечная прямоугольная ямама (1)(1)
|
0 |
при |
0 x L |
|
|
|
|
U ( x) |
|
при |
x 0, x L |
|
|||
|
|
|
|
U U 0 U |
|
|
|
0 L X
2m (E U ) 0
2
Частица всегда находится в области 0 x L. Вне этой области 0. Запишем уравнение Шредингера для частицы, находящейся в области 0 x L.
d 2 |
|
2mE |
|
(2) |
|
dx2 |
2 |
||||
|
|
|
Волновая функция, являющаяся решением уравнения (2), имеет вид
Asin kx B cos kx, |
(3) |
k (2mE / 2 )1/ 2 . Из граничных условий (0) 0, (L) 0 и условий непрерывности волновой функции
имеем
Asin kL 0. |
(4) |
|
Из (4) следует |
|
|
kL n , |
n 1, 2,3 , |
(5) |
т. е. внутри ямы устанавливаются стоячие волны, а энергия состояния частиц имеет дискретный спектр значений En
E |
|
2 k2 |
|
2 2 n2 |
, |
(6) |
|
|
|||||
n |
|
2m |
|
2mL2 |
|
|
|
|
|
|
|
Бесконечная прямоугольная ямама (2)(2)
3 |
|
2 |
|
|
sin |
3 x |
E |
3 |
9 2 2 |
|||||||
|
L |
|
L |
|||||||||||||
|
|
|
|
|
|
|
|
|
2m L2 |
|||||||
2 |
|
2 |
|
|
sin |
|
2 x |
E |
2 |
|
4 2 2 |
|||||
|
|
L |
|
L |
2m L2 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
1 |
|
2 |
|
sin |
|
x |
E |
1 |
|
|
2 2 |
|
||||
|
|
|
|
|
|
|
|
|
||||||||
|
|
L |
|
L |
2m L2 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||
Частица может иметь только те значения энергии, которые определяются соотношением
(6). Об этой ситуации говорят, что энергия квантуется на дискретные уровни. Частица может находиться в каком-то одном из множества дискретных состояний, доступных для неё. Чтобы частица перешла на другой энергетический уровень, она должна приобрести или потерять некоторое количество энергии, равное разности энергий уровней, между которыми происходит переход.
Энергии состояний растут квадратично в зависимости от квантового числа n. Каждому значению энергии соответствует волновая функция n (x) , которая с учетом условия
нормировки
L |
|
|
|
|
|
L |
|
|
|
nx |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
n ( x) |
|
2 |
dx |
|
|
A sin |
|
|
dx 1 |
|||
|
|
|
||||||||||||
|
|
|
L |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
имеет вид |
|
|
|
|
|
|
|
|
|
sin Lnx . |
||||
|
|
n ( x) |
|
|
2 |
|||||||||
|
|
|
|
L |
||||||||||