Вопрос 21

В курсе информатики подробно изучаются возможности табличного процессора Microsoft Excel. Представляется возможным при обучении математике реализовывать межпредметные связи, заключающиеся в применении математических методов с помощью пакета Excel. С его помощью можно вычислять значения линейных, показательных, логарифмических, тригонометрических функций и  на основании этих расчетов строить и преобразовывать графики функций. Основное достоинство такого представления – наглядность. На графиках легко просматривается тенденция к изменению.

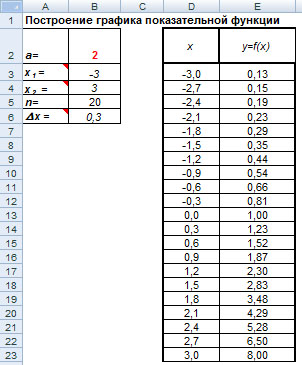Построение графика функции с помощью табличного процессора Excel начинается с занесения исходных числовых данных. Подробнее рассмотрим построение графика  показательной функции. Для этого требуется ввести основание показательной функции. Далее необходимо определить левую и правую границы области построения, количество интервалов табуляции, рассчитать шаг табуляции по формуле: =(B4-B3)/B5 .

Далее заполним таблицу данных, содержащую пару колонок Абсцисса иОрдината. В первую ячейку колонки Абсцисса скопируем содержимое ячейки левой границы области построения, введя в ячейку формулу: =B3. В следующей ячейке колонки произведем расчет следующего значения абсциссы, прибавив шаг табуляции: =C2+$B$6. Скопируем формулу из ячейки C3 в диапазон ячеекC4:C21 с помощью маркера автозаполнения в правом нижнем углу курсора.Колонка Абсцисса заполнена.

Далее в ячейки колонки Ордината занесем формулы, позволяющие рассчитать значение показательной функции в каждой точке. Для вычисления в ячейку D2 введем формулу:=$B$2^C2, скопируем ее в ячейки D3:D21.

Полученная таблица данных содержит один ряд данных C2:D21 для построения графика видаy=f(x).

Для построения графика показательной функции выделим диапазон ячеек, содержащий данные для построения графика (C2:D21), запустим Мастер диаграмм.

В диалоговом окне Тип диаграммы выберем Точечная, вид «Точечная диаграмма со значениями, соединенными сглаживающими линиями без маркеров».

В окне Источник данных диаграммы на вкладке Диапазон данных проверим, что диапазон выбран правильно и установлен флажок опции «Ряды в столбцах». .

В окне П араметры диаграммы на вкладке Заголовкивведем в поле Название диаграммы – «График показательной функции», в поле Ось Х (категорий) – «x», в поле Ось Y (значений) – «y». На вкладке Линии сетки отключим основные и промежуточные линии сетки по каждой из осей.

 Выберем расположение диаграммы на отдельном листе и введем имя листа График в соответствующем поле. Нажимаем кнопку Готово.

Выделм правой кнопкой ось y и из контекстного меню выполним команду Формат оси. На вкладке Число установим число десятичных знаков 0.

С помощью команды контекстного меню Формат рядов данных… можно изменить толщину, цвет линии графика, размещение и выравнивание названий осей.

Изменяя основание функции, легко проследить за преобразованием графика, определить, как зависит угловой коэффициент касательной к графику в точке x₀=0 от основания, как при этом меняются свойства функции.