
- •Глава 9. Магнитные цепи
- •9.1. Основные понятия и величины, характеризующие магнитное поле. Закон полного тока
- •9.2 Основные характеристики ферромагнитных материалов
- •9.3. Магнитная цепь
- •9.4. Законы магнитной цепи
- •9.5. Расчет неразветвленных магнитных цепей
- •9.5.1. Расчетная аналогия между магнитными и электрическими цепями
- •9.5.2. Определение мдс по заданному магнитному потоку
- •9.5.3. Определение магнитного потока по заданной мдс
- •9.6. Расчет разветвленных магнитных цепей
9.5. Расчет неразветвленных магнитных цепей
9.5.1. Расчетная аналогия между магнитными и электрическими цепями
Все методы расчета
электрических цепей с нелинейными
сопротивлениями полностью применимы
и к расчету магнитных цепей, так как и
магнитные и электрические цепи подчиняются
одним и тем же законам – законам Кирхгофа.
Аналогом тока I
в электрической цепи является поток Ф
в магнитной цепи. Аналогом ЭДС Е
является МДС F.
Аналогом ВАХ нелинейного сопротивления
I(U)
– вебер-амперная
характеристика
участка магнитной цепи
![]() .
.
Однако расчетная
аналогия между электрическими и
магнитными цепями не распространяется
на физические процессы. В отличие от
ЭДС, которая движет в проводниках
элементарные заряды, МДС никакого
движения не вызывает. В соответствии с
законом Джоуля-Ленца в электрической
цепи происходит непрерывная затрата
электрической энергии; постоянное
магнитное поле, раз созданное, не требует
энергии для своего поддержания. В
электрической цепи возможно существование
ЭДС без тока, когда цепь разомкнута и
![]() ,
в магнитной цепи при наличии МДС всегда
существует магнитный поток, т.е. магнитное
сопротивление
в бесконечность не обращается.
,
в магнитной цепи при наличии МДС всегда
существует магнитный поток, т.е. магнитное
сопротивление
в бесконечность не обращается.
При расчете неразветвленных магнитных цепей существует два вида задач: прямая задача – определение потока в магнитной цепи по заданной МДС; обратная задача – определение МДС по заданному магнитному потоку.
9.5.2. Определение мдс по заданному магнитному потоку
Заданы: конфигурация и геометрические размеры магнитной цепи (рис. 9.11, а); кривые намагничивания ферромагнитных материалов; магнитный поток или магнитная индукция в каком-нибудь сечении.
Требуется определить МДС, ток или w намагничивающей обмотки (обратная задача).
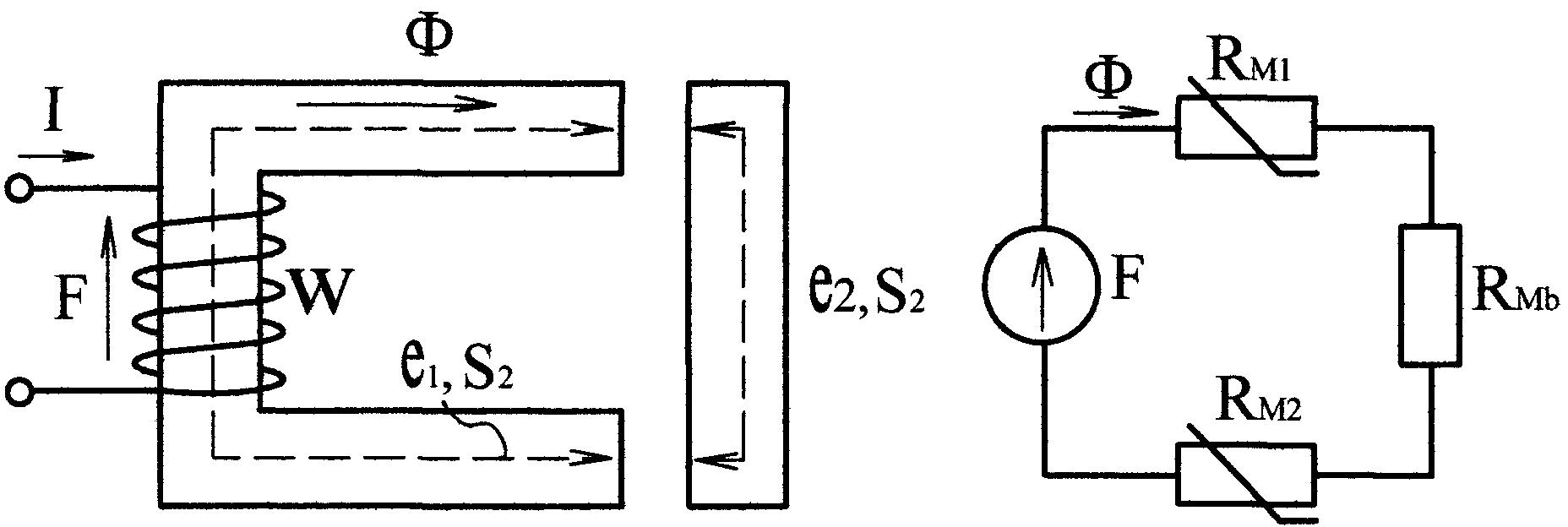
а) б)
Рис. 9.11
Расчет проводим в следующей последовательности:
Разбиваем магнитную цепь на участки постоянного сечения (
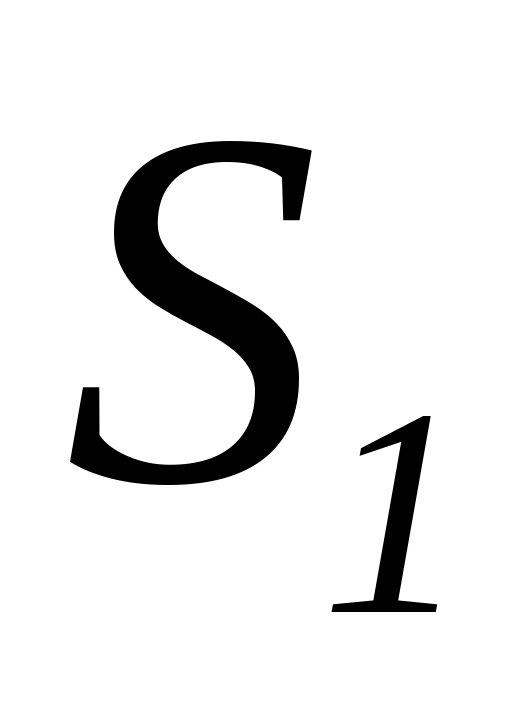 ,
,
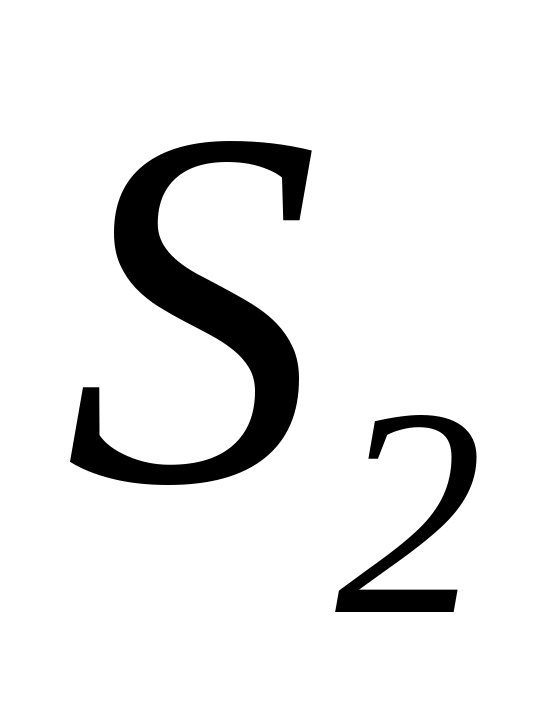 ,
,
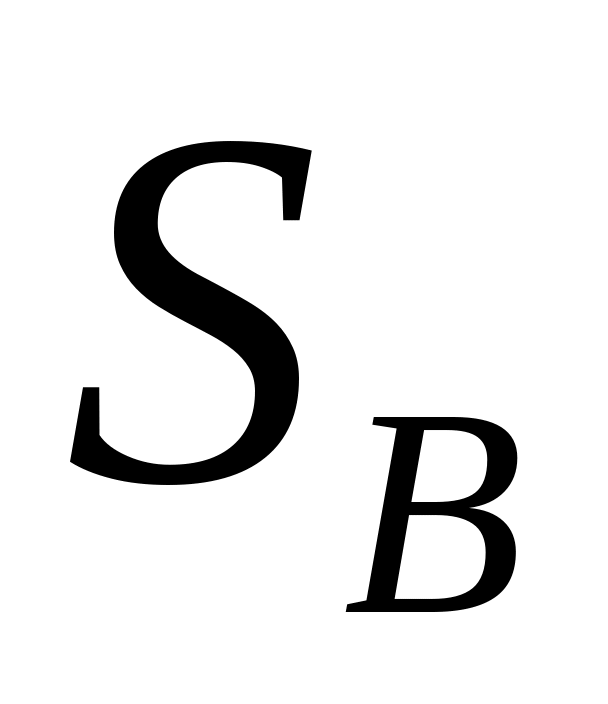 )
и определяем длины (
)
и определяем длины (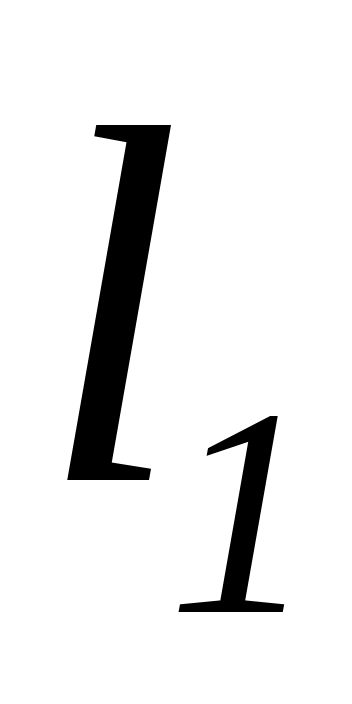 ,
,
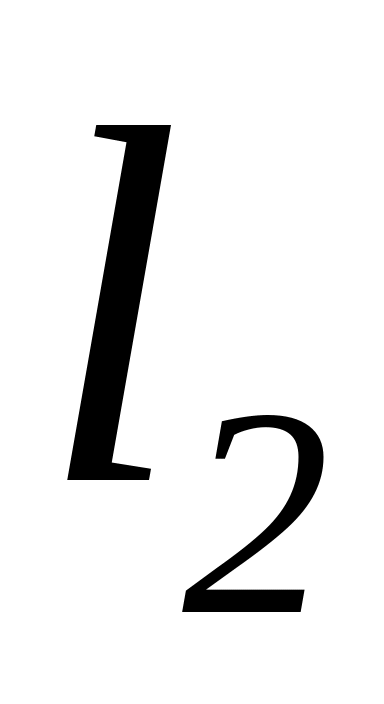 ,
,
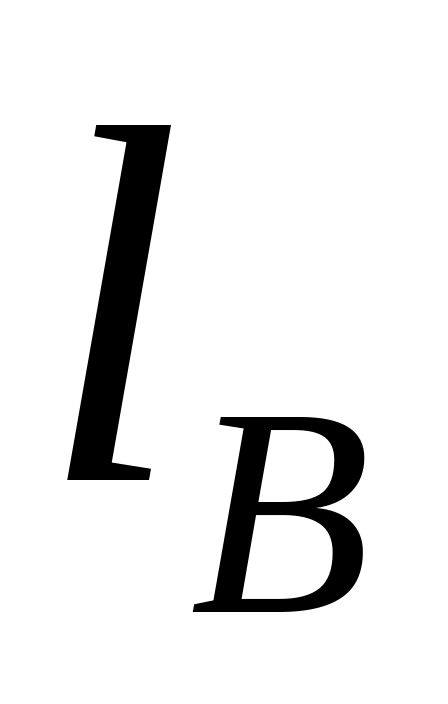 )
и площади поперечного сечения участков.
Длины участков берем по средней длине
магнитной линии.
)
и площади поперечного сечения участков.
Длины участков берем по средней длине
магнитной линии.
При малой длине воздушного зазора магнитное поле в зазоре можно считать однородным, а его сечение – равным сечению сердечника .
Магнитную цепь представляем эквивалентной схемой (рис. 9.11, б).
Составляем уравнение для магнитной цепи по второму закону Кирхгофа:
![]() .
.
Исходя из постоянства магнитного потока вдоль всей цепи (потоками рассеяния пренебрегаем), по заданному потоку и сечениям
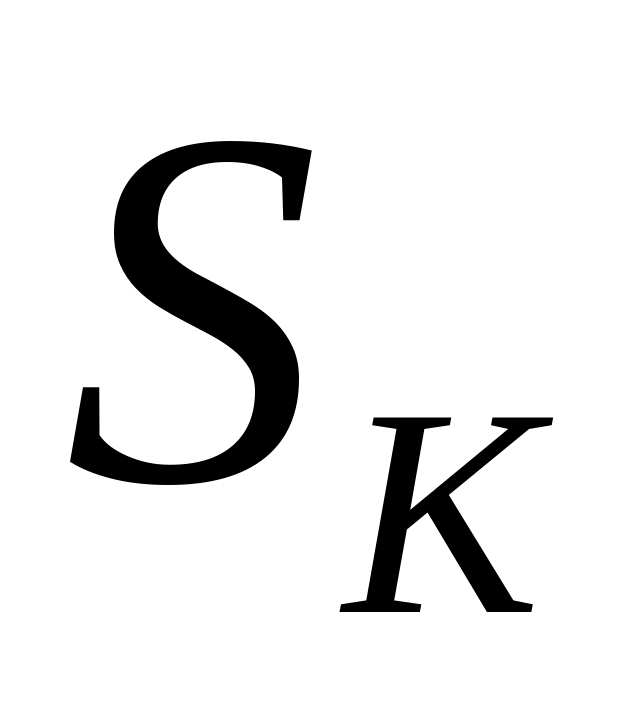 находим магнитные индукции на каждом
участке:
находим магнитные индукции на каждом
участке:
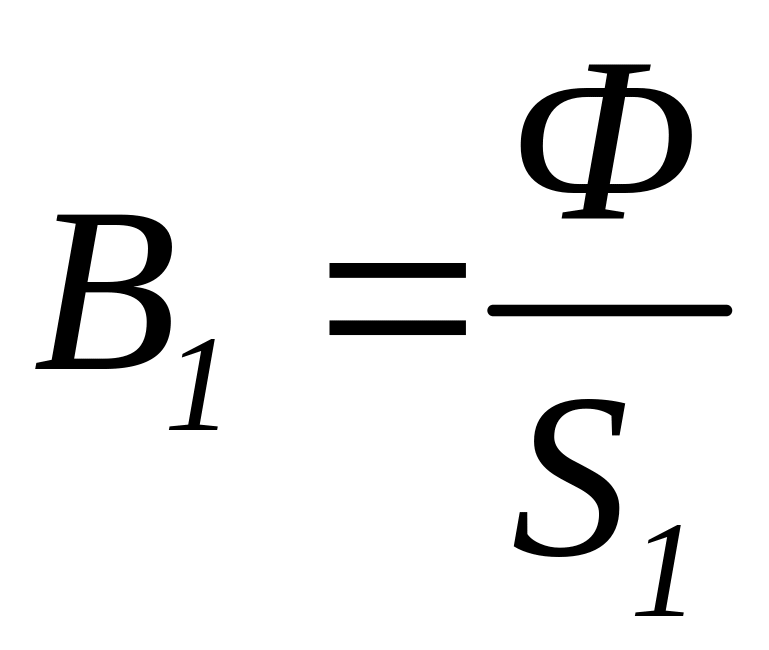 ;
;
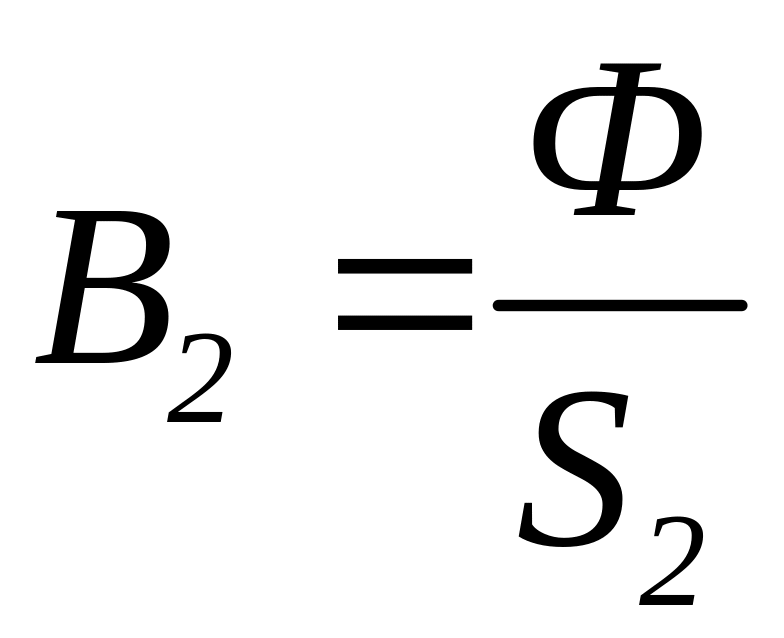 ;
;
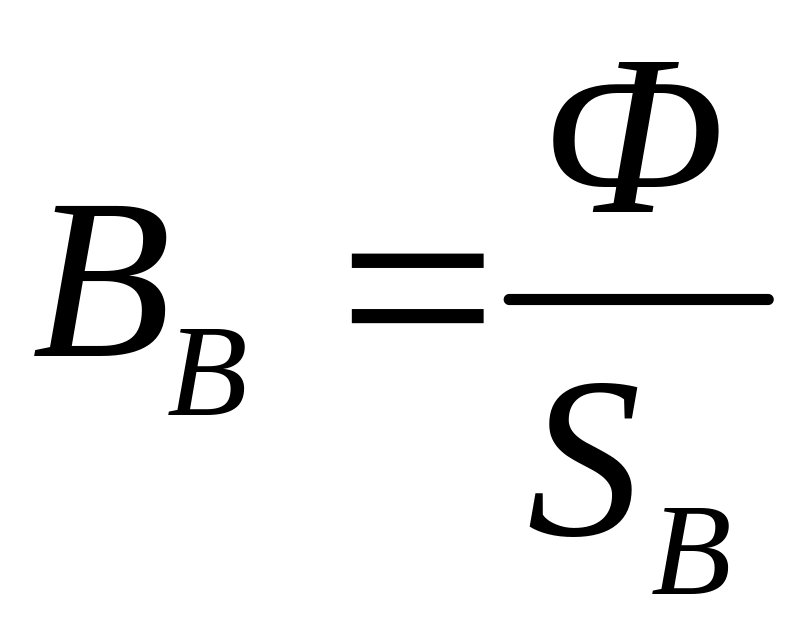 .
.
По кривым намагничивания определяем напряженности магнитного поля для ферромагнитных участков
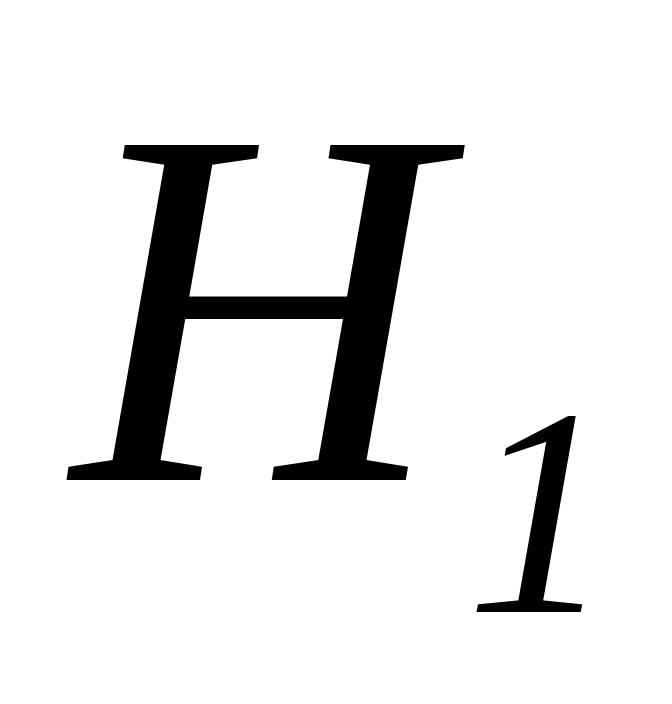 и
и
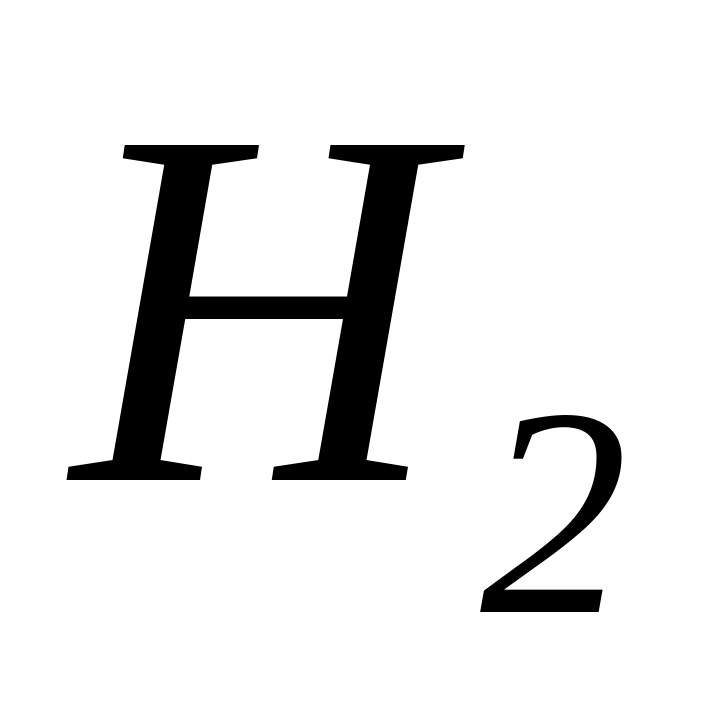 магнитной цепи. Напряженность в воздушном
зазоре определяем по формуле:
магнитной цепи. Напряженность в воздушном
зазоре определяем по формуле:
.
Подсчитываем сумму падений магнитных напряжений вдоль всей магнитной цепи
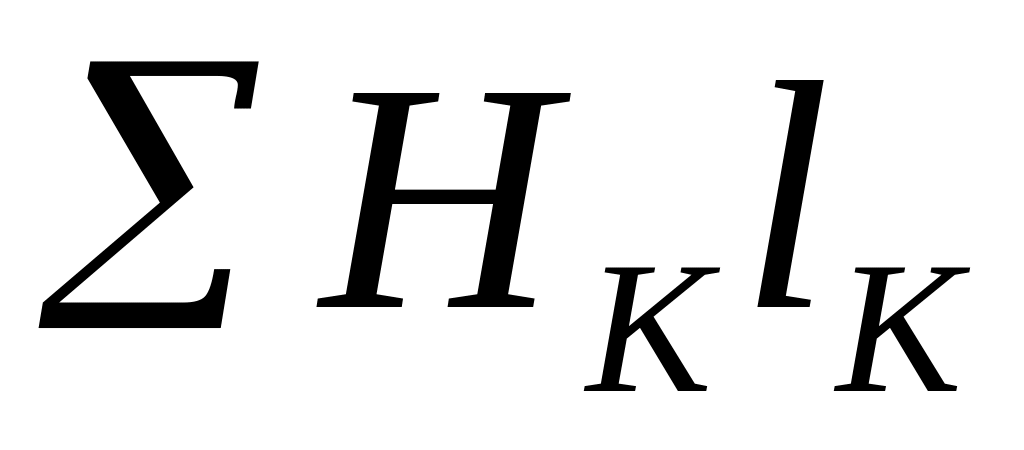 ,
равную МДС F.
Определив МДС
,
равную МДС F.
Определив МДС
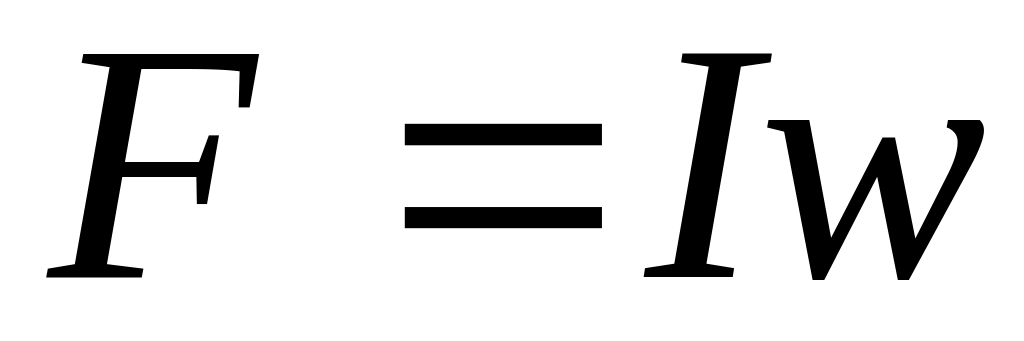 ,
можно найти ток I
при известном w
или w
при известном токе I.
,
можно найти ток I
при известном w
или w
при известном токе I.
Основным допущением расчета является то, что магнитный поток вдоль всей магнитной цепи полагается неизменным. В действительности небольшая часть потока всегда замыкается, минуя основной путь (поток рассеяния).
