Атом – наименьшая частица химического элемента, носитель его свойств. Является самой простой электро енйтральной химической микросистемой, подчиняющейся законам квантовой механики.

Для электрона в атоме справедлив принцип двойственности: электрон является одновременно и материальной частицей малой массы и электромагнитной волной.

Принцип неопределнности Гейзенберга: В каждый конкретный момент времени нельзя с одинаковой точностью определить место нахождения электронов (координаты x,y,z) и его скорость (или импульс).

Движение электорона в атоме может быть представлено в виде электронного облака.

Область электронного облака, в которой электрон проводит более 95% времени нывается электронной орбиталью (Э.О.). Больший размер орбитали характеризует большую энергию электрона. Орбитали близкого размера образуют энергетические уровни, которые состоят из подуровней.

Для описания состояния электрона в атоме используются 4 квантовых числа (n,l,m,s). Первые три соответствуют трем степеням свободы электрона в трехмерном пространстве, а четвертое соответсвует вероятности вращения электрона вокруг воображаемой собственной оси. Квантовые числа:

1. “n” – главное квантовое число. Характеризует уровень энергии электрона в поле атома (удаленность от ядра). Математическая зависимость энергии связи с ядром: E_a=-13,6/n² Эв, n=1,2,… Для реальных элементов n=1,…,7. n=номеру периода.

2. “l” – орбитальное квантовое число. Характризует тип подуровня (форма электронного облака). l=0,1,2,…,(n-1). Обозначается буквами. При этом l=0 соответствует s, 1-p, 2-d, 3-f, 4-q, 5-h.

3. “m” – магнитное квантовое число. Характеризует пространственное расположение орбитали. m= 0,  1,  2,…,  l. Cумма орбиталей на подуровне:  =2l+1.

4. “s” – спиновое квантовое число. Характеризует вероятность вращения электрона вокруг своей оси в двух противоположенных направлениях. s= 1/2. “+” – по часовой стрелке, “-“ – против часовой стрелке. Вращение сообщает электрону собственный магнитный момент, который называется спином электрона.

Принцип Паули (запрет): у атомов, имеющих больше одного электрна не может быть двух электронов с одинаковыми значениями всех четырех квантовых чисел. Или так: на одной орбитали могут находится только два электрона, причем с противоположенными спинами.

Принцип минимума энергии: последовательное заполенние электронов в атоме должно отвечать как минимому энергии самого электрона, так и минимому энерги атома в целом. Или так: минимум энергии соответствует максимому устойчивости. Заполение идет в соответсвии с уравнением энергии орбитали: ns<(n-1)d (n-2)f<np. На внешнем уровне не может быть более 8 электронов.

Правило Клечковского: сначала заполняются те подуровни, сумма n+l которых наименьшая. Если для двух подуровней сумма n+l равна, то сначала заполняется подуровень с меньшим n.

Правило Хунда: в основном (невозбужденном) состоянии атома на подуровнях np, nd и nf всегда имеется максимальное количество неспаренных электронов (максимальный неспаренный спин).

Подуровни p, d и f состоят из нескольких орбиталей, энергия которых одинакова, поэтому эти подуровни называются “вырожденными”: p подуровень вырожден трехкратно, d пятикратно и f семикратно. Для электронов этих подуровней соблюдается правило Хунда.

Валентность – способность образовывать химические связи.

Основное состояние – состояние с минимальной энергией, т.е электроны находятся ближе к ядру.

Возбужденное состояние – состояние, при котором все или часть электронов в атоме распарены и находятся на подуровне с большей энергией, т.е дальше от ядра.

Максимальная валентность наблюдается в возбужденном состоянии и как правило совпадает с номером группы, в которой находится элемент.

В изолированном атоме электроны могут находиться только в определенных квантовых состояниях. Каждое состояние, в котором в соответствии с принципом Паули может находиться только один электрон, определяется набором четырех квантовых чисел (главного n, орбитального l, магнитного m_l и магнитного спинового m_s) и имеет соответствующий энергетический уровень. Так как квантовые числа принимают только дискретные (определенные) значения (n = 1,2,3,…;  l = 0,1,2,…,n1;  m_l = 0, 1, 2, …l;  m_s = 1/2), то и энергетический спектр электронов в атоме является дискретным и состоит из ряда разрешенных энергетических уровней. Разрешенные уровни энергии отделяются друг от друга областями запрещенных энергий. В соответствии с принципом минимума энергииэлектроны в атоме занимают нижние энергетические уровни, верхние – остаются свободными.

В отсутствии внешних полей (электрического или магнитного) значение энергии квантового состояния изолированного атома определяется квантовыми числами n и l. Квантовые состояния электрона, соответствующие числам m_l иm_s имеют одинаковую энергию. Такие состояния и соответствующие им уровни энергии называютсявырожденными. В изолированном атоме в вырожденных состояниях с орбитальным числом l может находиться 2(2l+1) электронов. Это число называется кратностью вырождениясостояния (уровня).

При сближении атомов до расстояний, на которых они находятся в твердом теле, взаимодействие между атомами достигнет значительной величины, и электроны каждого атома окажутся в электрическом поле не только своего ядра, но и во внешнем поле соседних ядер. Известно, что электрическое поле снимает вырождение состояний электронов. В кристалле взаимодействие между атомами приводит к снятию вырождения, связанного с квантовыми числами n, l и m_l. Квантовые состояния, связанные с ориентацией спина, от электрического поля практически не зависят. Поэтому каждый уровень энергии в твердом теле двукратно вырожден и содержит (или может содержать) два электрона с разной ориентацией спина. Снятие вырождения с энергетических состояний приводит к расщеплению уровней энергии электронов и образованию энергетической зоны, состоящей из дискретных подуровней, на каждом из которых может находиться по два электрона. Зоны разрешенных энергий отделяются друг от друга зонами запрещенных энергий (запрещенными зонами).

Из рис.1, на котором показано расщепление уровней как функции расстояния r между атомами, видно, что заметно расщепляются и расширяются лишь уровни внешних валентных электронов, наиболее слабо связанных с ядром и имеющих наибольшую энергию, а также более высокие уровни, которые в основном состоянии атома вообще электронами не заняты. Уровни же внутренних электронов либо совсем не расщепляются, либо расщепляются слабо. Таким образом, в твердых телах внутренние электроны ведут себя так же, как в изолированных атомах, валентные же электроны «коллективизированы»  принадлежат всему твердому телу.

 

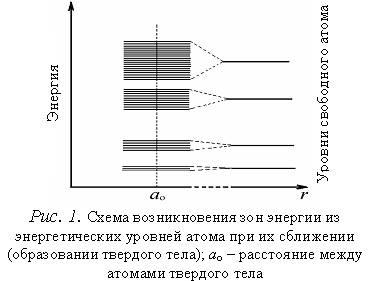
Заполнение энергетических зон электронами различно. Зоны, образованные из энергетических уровней внутренних электронов атомов, заполнены полностью. На физические свойства твердых тел эти зоны не оказывают заметного влияния. На схемах энергетических зон (энергетических диаграммах) они обычно не изображаются. Энергетическая зона, образованная из энергетических уровней внешних валентных электронов атомов, находящихся в основном состоянии, называется валентной зоной. Выше валентной зоны в энергетическом спектре электронов располагаются зоны, образованные из пустых энергетических уровней атомов (зоны проводимости). 

Многоэлектронные атомы. Заполнение электронных оболочек Конспект лекции (с демонстрациями)

Аннотация: Оценка энергии и размера атомов. Распределение электронов в атоме по возможным квантовым состояниям (с дополнением демонстрацией на компьютерной модели).

Оценка энергии атомов в основном состоянии

Начнем с оценки энергии атома гелия (Физика за рубежом. 1988. Серия Б (преподавание): Сборник статей. М.:Мир, 1988, стр.130), основанной на использовании соотношения неопределенности Гейзенберга . В атоме гелия имеется два электрона с антипараллельными спинами. Их будем рассматривать как сферическое электронное облако со средним радиусом R. Минимальную кинетическую энергию электрона T, находящегося в объеме с линейным размером R оценим по формуле

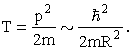
Полная энергия атома складывается из энергии притяжения электронов к ядру (знак минус), энергии отталкивания электронов друг от друга и кинетической энергии электронов

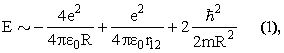
где определим, что 1/R - среднее значение величины, обратной расстоянию электронов от ядра и 1/r₁₂ - среднее значение величины, обратной расстоянию между электронами. Положим

причем β будет меньше единицы, т.к. r₁₂ больше среднего расстояния электронов от ядра R. Запишем выражение (1) в виде

где A = (4 - β)e², B = 2h²/4π²m, и найдем значение R, при котором энергия минимальна (приравняв производную от E по R нулю). Это значение R = B/A. Теперь имеем для основного состояния

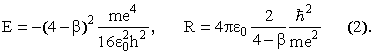
Осталось определить значение β = R/r₁₂. Обе величины R и r₁₂ определяются плотностью распределения электронов в пространстве p(r). Радиус R найдем интегрированием R^-1 = 4π∫(p(r)/r)r²dr, а r₁₂ через распределение потенциала U(r), создаваемое распределением заряда ep(r). Тогда

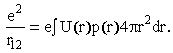
Простейший случай - прямоугольное распределение заряда (рисунок справа). Несложные вычисления дают значение β = 0.8. Для экспоненциального распределения p(r) ~ exp(r/b) величина β = 5/8.

Подстановка β = 0.8 в выражение (2) дает E = -5.1·13.6 эВ, для β = 5/8 получаем E = -5.7·13.6 эВ. Точный расчет энергии, необходимой для удаления обоих электронов атома гелия, дает E = -5.81·13.6 = 79.0 эВ. Удивительно: проведена грубая оценка, а получен такой близкий к точному результат. Энергия связи электрона в ионе гелия He⁺ равна 4·13.6 эВ, следовательно, энергия ионизации атома 24.6 эВ.

Таким же методом можно сделать оценки и для атомов с большим числом электронов Z. Есть одна тонкость в этом случае, связанная с принципом Паули: в атоме может быть только один электрон с данным набором квантовых чисел. Разделим весь объем атома на ячейки с линейным размером r₀, которую могут занимать два электрона с антипараллельными спинами. Потребуется Z/2 таких ячеек, так что (Z/2)r₀³ = R³. И оценивать минимальную кинетическую энергию электрона с помощью соотношения неопределенности будем, полагая что электрон движется в объеме с линейным размером r₀

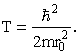
Если Z >> 1 выражение (1) следует заменить на

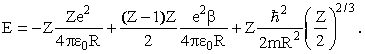
Здесь первое слагаемое - энергия притяжения Z электронов к ядру, второе - энергия отталкивания (Z-1)Z/2 электронных пар (попрежнему R/β - среднее расстояние между электронами), третье - оценка суммарной кинетической энергии всех электронов. Заменив Z(Z-1) на Z², получим

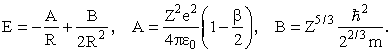
Значение R, при котором энергия минимальна, и минимальное значение энергии равны, соответственно,

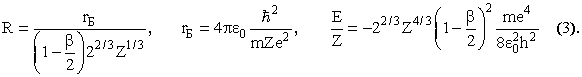
В этих формулах r_Б - боровский радиус, равный 0.53·10^-10 м. Для определения β задаемся распределением электронной плотности

Множитель 1/rⁿ обеспечит правильное поведение распределения у ядра, экспонента - убывание плотности при удалении от ядра. Постоянные A, n и b определяются из условий: нормировки (всего имеется Z электронов), того, что на K-оболочке (n = 1) находится два электрона, и равенства среднего < r^-1 > = R^-1. Итог вычислений - β = 1 - 2/π = 0.36. Подставив это значение в (3), получаем среднее расстояние электронов от ядра R и среднюю энергию связи электрона в атоме E/Z.

Cреднее расстояние электронов от ядра R меньше размера атома R_а, так как большинство электронов находится на внутренних оболочках. Размер атома R_а можно оценить, используя распределение электронной плотности p(r) и, оказывается, что он слабо зависит от Z, что показывают данные таблицы:

Z	Rа/rБ
30	2.49
50	2.33
90	2.13

Бóльший заряд ядра приводит к слабому уменьшению размера атома и увеличению энергии связи электронов.