(НЕ обязательно)Степень искривленности ПЛОСКОЙ кривой характеризуется кривизной
Пусть точка движется по окружности с центром О. За время t она пришла из А в A”.Тогда t = t” – t. При произвольном движении в течение очень малого промежутка времени точка движется по окружности, затем переходит на другую окружность и т.д. Взятие предела в определении кривизны позволяет считать данный участок дугой окружности
Билет №2. Кинематика вращательного движения: угловая скорость и угловое ускорение, их связь с линейной скоростью и ускорением.
Угловая скорость:
Выберем на окружности точку 1. Построим радиус. За единицу времени точка
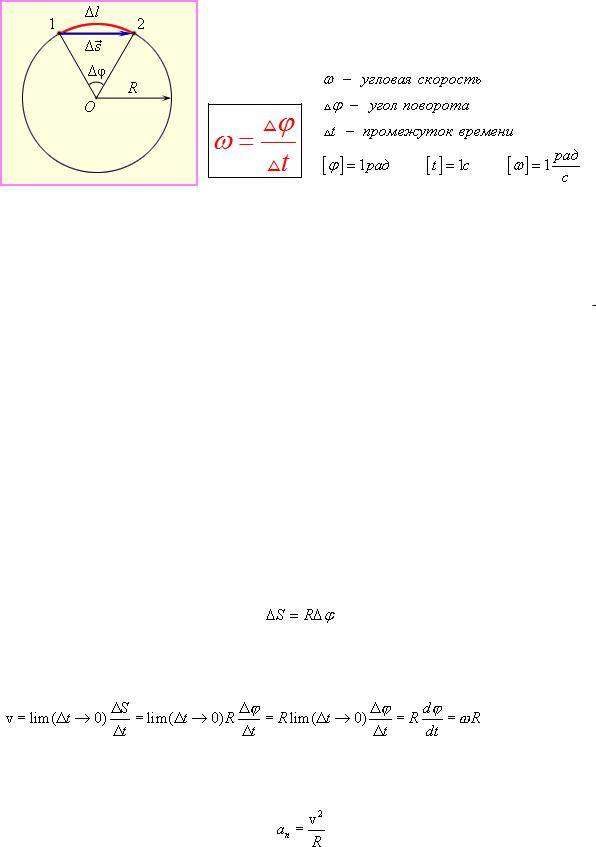
переместится в пункт 2. При этом радиус описывает угол. Угловая скорость численно равна углу поворота радиуса за единицу времени.
Угловое ускорение:
Величина, характеризующая быстроту изменения угловой скорости (См. Угловая скорость) твердого тела. При вращении тела вокруг неподвижной оси, когда его угловая скорость ω растет (или убывает) равномерно, численно У. у. ε = ω/Δt, где ω
— приращение, которое получает ω за промежуток времени Δt, а в общем случае при вращении вокруг неподвижной оси ε = dω/dtdt = d 2φ/dtdt2, где φ — угол поворота тела. Вектор У. у. ε направлен вдоль оси вращения (в сторону ω при ускоренном вращении и противоположно ω — при замедленном). При вращении вокруг неподвижной точки вектор У. у. определяется как первая производная от вектора угловой скорости ω по времени, т. е. ε = dω/dtdt, и направлен по касательной к Годографу вектора ω в соответствующей его точке. Размерность У. у. Т-2.
Связь угловых и линейных величин:
Отдельные точки вращающегося тела имеют различные линейные скорости 
. Скорость каждой точки, будучи направлена по касательной к соответствующей окружности, непрерывно изменяет свое направление. Величина скорости 
определяется скоростью вращения тела 
и расстоянием R рассматриваемой точки от оси вращения. Пусть за малый промежуток времени 
тело повернулось на угол 
(рис 2.4). Точка, находящаяся на расстоянии R от оси проходит при этом путь, равный
Линейная скорость точки по определению:
(2.6)
Найдем линейные ускорения точек вращающегося тела. Нормальное ускорение:
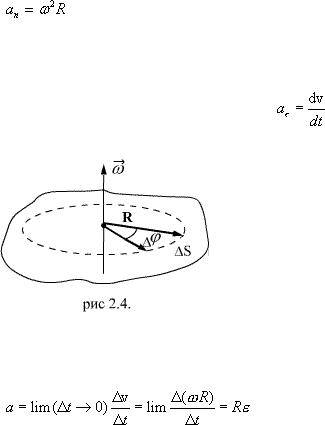
подставляя значение скорости из (2.6), находим:
(2.7)
Тангенциальное ускорение:
Воспользовавшись тем же отношением (2.6) получаем
(2.8)
Таким образом, как нормальное, так и, тангенциальное ускорения растут линейно с расстоянием точки от оси вращения.
Билет №3. Инерциальные системы отсчета и первый закон Ньютона. Второй закон Ньютона. Масса, импульс, сила.
ПЕРВЫЙ ЗАКОН НЬЮТОНА Первый закон Ньютона: всякая материальная точка (тело) сохраняет состояние
покоя, если силы скомпенсированы, или равномерного прямолинейного движения до тех пор, пока воздействие со стороны других тел не заставит её (его) изменить это состояние. (ускорение тела равно нулю)
Стремление тела сохранить состояние покоя или равномерного прямолинейного движения называется инертностью. Поэтому первый закон Ньютона называют
законом инерции.
Первый закон Ньютона выполняется только в инерциальной системе отсчета (ИСО). Таким образом, первый закон Ньютона утверждает существование инерциальных
систем отсчёта
Как раз Сутью первого закона является утверждение, что инерциальные системы отсчета существуют
Сущность первого закона Ньютона может быть сведена к трем основным положениям:
1.все тела обладают свойствами инерции (Инерция – это явление, при котором тело стремится сохранить свое первоначальное состояние) ;
2.существуют инерциальные системы отсчёта, в которых выполняется первый закон Ньютона;
3.движение относительно. Если тело А движется относительно тела отсчета В со скоростью υ, то и тело В, в свою очередь, движется относительно тела А с той же скоростью, но в обратном направлении υ = – υ'.
2 Инерциа́льная систе́ма отсчёта (ИСО) — система отсчёта, в которой все свободные тела (материальные точки), свободные от внешних воздействий, движутся прямолинейно и равномерно, либо покоятся.
Если тело движется и на него не действуют другие тела, то движение будет сохраняться, оно будет оставаться прямолинейным и равномерным. Если же на тело не действуют другие тела, а тело покоится, то будет сохраняться состояние покоя.
Признаки:
1. Отсутствие ускорения.
Масса, сила.
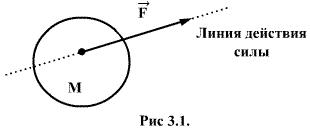
Сила – векторная величина, характеризующая меру взаимодействия между телами. Сила F полностью определена, если заданы ее модуль, направление в пространстве и точка приложения. Прямая, вдоль которой направлена сила, называется линией действия силы.
Механическое взаимодействие может осуществляться как при непосредственном контакте тел (трение, давление тел друг на друга), так и между удаленными телами (притяжение планет к Солнцу, взаимодействие заряженных тел).
Масса – мера инертности тела. В механике Ньютона масса – величина: скалярная, положительная (m > 0), аддитивная (m = ∑mi),постоянная(m=const),[m]=кг.), постоянная (m = const), [m]=кг.m] = кг.
ВТОРОЙ ЗАКОН НЬЮТОНА.(при m=const)