Билет №19. Квазистатические процессы. Уравнение состояния в термодинамике. Обратимые и необратимые процессы.
Квазистатический процесс в термодинамике— идеализированный процесс, состоящий из непрерывно следующих друг за другом квазистатических состояний, в которых характеризующие систему термодинамические величины за время наблюдения не изменяются. Если каждое такое квазистатическое состояние системы близко к состоянию равновесия и, следовательно, систему в каждый момент времени можно считать находящейся в термодинамическом равновесии, то такие процессы называют равновесными, или, точнее, квазиравновесными.
Значение квазистатических процессов состоит в том, что они сильно упрощают термодинамические исследования. Это объясняется тем, что для мгновенного описания состояния системы, совершающей квазистатический процесс, требуется столько же параметров, сколько и для описания равновесного состояния. В случае газа таких параметров два, например объём и температура.
Квазистатические процессы в строгом смысле этого слова никогда не реализуются в природе. Они являются абстракциями. Но к ним можно подойти сколь угодно близко. Очень многие реальные процессы, идущие с конечными скоростями, часто могут считаться приблизительно квазистатическими.
Простейшей идеализированной моделью вещества является идеальный газ. Идеальный газ это газ, в котором взаимодействие между молекулами пренебрежимо мало, а размеры молекул много меньше размеров сосуда.
Для описания сложной системы (термодинамической системы), состоящей из большого числа молекул, используют усреднённые параметры системы. Основные из них это объём, давление и температура.
Уравнение состояния – функциональная зависимость между параметрами состояния при равновесии. Приведём общий вид уравнения состояния термодинамической системы F (P ,V ,T )=0
Конкретный вид уравнения зависит от физических свойств рассматриваемой системы. Многочисленные экспериментальные данные свидетельствуют, что большинство газов при нормальных условиях с достаточной точностью могут быть описаны уравнением состояния идеального газа.
Уравнение состояния идеального газа (уравнение Менделеева – Клапейрона)
pV =vRT или pV = m RT |
, |
μ |
|
где v= mμ – количество вещества; Т – термодинамическая температура; V – объём,
занимаемый газом; P – давление газа; m – масса газа; – молярная масса газа; R – универсальная газовая постоянная, R = 8,31 Дж /(мольК).
Универсальная газовая постоянная – это физическая величина, характеризующая работу одного моля газа при его изобарном нагревании на один Кельвин.
Другая форма уравнения состояния: P=nkT где k – постоянная Больцмана, выражающая соотношение между единицей энергии и единицей температуры, k = 1.38·10-23Дж/К, Т – температура, выраженная в Кельвинах.
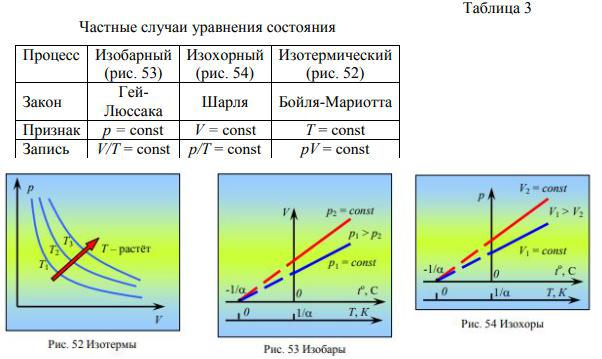
Процессы изменения состояния термодинамической системы, протекающие при неизменной массе и постоянном значении одного из параметров состояния, называют изопроцессы. Все законы идеальных газов для изопроцессов могут быть получены из уравнения состояния идеального газа (см. табл. 3).
Термодинамический процесс называется обратимым, если он может происходить как в прямом, так и в обратном направлении, причем если такой процесс происходит сначала в прямом, а затем в обратном направлении и система возвращается в исходное состояние, то в окружающей среде и в этой системе не происходит никаких изменений.
Всякий процесс, не удовлетворяющий этим условиям, является необратимым.
Билет №20. Работа, внутренняя энергия, количество теплоты. Первое начало термодинамики.Теплоемкость. Уравнение Майера.
1.Внутренняя энергия в термодинамике
Внутренней энергией тела называется сумма кинетических энергий хаотического движения молекул и потенциальных энергий их взаимодействия друг с другом. Кинетическая энергия тела как целого (или например энергия ветра) во внутреннюю энергию не входит.
Внутренняя энергия тела является аддитивной величиной, т.е. внутренняя энергия всего тела равна сумме энергий его частей.
Внутренняя энергия тела является функцией состояния системы. Это значит, что, каким бы способом мы ни привели систему в некое состояние, энергия всегда будет одной и той же, т.е. изменение внутренней энергии при переходе из одного состояния в другое всегда равна разности энергий в этих двух состояниях и не зависит от процесса перехода.
2.Работа в термодинамике
При перемещении поршня сечением S в цилиндре газ совершает работу, равную произведению силы F на перемещение. Сила связана с давлением р известным соотношением F = pS.
Интегрирование дает работу при переходе из начального состояния с объемом V1 в конечное состояние с объемом V2
3.Количество теплоты в термодинамике.
Коли́чество теплоты́— энергия, которую получает или теряет тело при теплопередаче.
Количество теплоты входит в математическую формулировку первого начала термодинамики 
Количество теплоты является функцией процесса, а не функцией состояния, то есть количество теплоты, полученное системой, зависит от способа, которым она была приведена в текущее состояние
4.Первое начало термодинамики.
5.Теплоемкость.
