
- •Билет №1. Основные кинематические характеристики криволинейного движения: скорость и ускорение. Нормальное и тангенциальное ускорение.
- •Основные характеристики криволинейного движения:
- •2. УСКОРЕНИЕ
- •4.НОРМАЛЬНОЕ УСКОРЕНИЕ
- •Билет №2. Кинематика вращательного движения: угловая скорость и угловое ускорение, их связь с линейной скоростью и ускорением.
- •Билет №3. Инерциальные системы отсчета и первый закон Ньютона. Второй закон Ньютона. Масса, импульс, сила.
- •Билет №4. Закон сохранения импульса. Упругое и неупругое взаимодействие.
- •Билет №5. Уравнение движения материальной точки. Третий закон Ньютона. Силы трения. Сила упругости.
- •Уравнение движения материальной точки
- •Векторный способ описания движения
- •Координатный способ описания движения
- •Естественный способ описания движения
- •Третий закон Ньютона
- •Силы трения
- •Виды трения:
- •Сила упругости
- •Закон Гука
- •Билет №6. Закон всемирного тяготения. Зависимость ускорения свободного падения от высоты. Первая космическая скорость.
- •Билет №7. Сила, работа и потенциальная энергия. Консервативные и неконсервативные силы. Работа и кинетическая энергия. Закон сохранения полной механической энергии в поле потенциальных сил.
- •Дополнительная информация:
- •Ответ:
- •СИЛА (консервативные и неконсервативные силы)
- •Работа (работа, кинетическая энергия и потенциальная энергия)
- •Закон сохранения полной механической энергии в поле потенциальных сил.
- •Билет №8. Момент импульса материальной точки и механической системы. Момент силы. Уравнение моментов. Закон сохранения момента импульса механической системы.
- •Момент силы
- •Момент импульса материальной точки и механической системы.
- •Уравнение моментов.
- •Закон сохранения момента импульса механической системы.
- •Билет №9. Момент импульса тела. Момент инерции. Основное уравнение динамики вращательного движения твердого тела с закрепленной осью вращения.
- •Билет №10.Теорема Штейнера. Доказательство. Примеры использования.
- •Билет №11. Кинетическая энергия твердого тела при вращении
- •Билет №12. Неинерциальные системы отсчета. Силы инерции. Отличие сил инерции от сил взаимодействия.
- •Билет №13. Кориолисово ускорение. Причина возникновения. Направление.
- •Билет №15. Постулаты специальной теории относительности (СТО) Эйнштейна. Относительность одновременности и преобразования Лоренца.
- •Билет №16. Парадоксы релятивистской кинематики: сокращение длины и замедление времени в движущихся системах отсчета.
- •Билет №17. Релятивистский импульс. Взаимосвязь массы и энергии в СТО.
- •Билет №18. Термодинамическое равновесие и температура. Эмпирическая температурная шкала. Нулевое начало термодинамики.
- •Билет №19. Квазистатические процессы. Уравнение состояния в термодинамике. Обратимые и необратимые процессы.
- •Билет №20. Работа, внутренняя энергия, количество теплоты. Первое начало термодинамики.Теплоемкость. Уравнение Майера.
- •Билет №21. Изохорический, изобарический, изотермический, адиабатический процессы в идеальных газах. Преобразование теплоты в механическую работу.
- •Билет №23. Энтропия. Второе начало термодинамики. Невозможность вечного двигателя второго рода.
- •Билет №24. Давление газа с точки зрения МКТ. Теплоемкость и число степеней свободы молекул газа.
- •Билет №25. Распределение Максвелла для модуля и проекций скорости молекул идеального газа. Экспериментальное обоснование распределения Максвелла.
- •Билет №26. Распределение Больцмана и барометрическая формула
- •Билет №27. Элементы физической кинетики, средняя длина свободного пробега. Явления переноса. Диффузия, теплопроводность, внутреннее трение. Броуновское движение.
- •Билет №28. Учет межмолекулярного взаимодействия в газах. Уравнение Ван-дер-Ваальса.
- •Билет №29. Изотермы реального газа. Двухфазные состояния. Внутренняя энергия реального газа.

Сила Кориолиса – еще одна сила инерции. Возникает при вращении СО. Вычисляется по формуле:
Fk=2 m v' х ωR
Так как мы живем на Земле, то её нужно учитывать:
●При свободном падении тел на них действует сила Кориолиса, направленная на восток.
●При выстреле вдоль меридиана на север, летящий снаряд будет отклоняться в северном полушарии ближе к востоку, а в южном – к западу.
●На тело, движущееся вдоль меридиана, всегда действует сила: в северном вправо, в южном – влево.
●Сила Кориолиса появляется при качании маятников. Во вращающейся СО поворачивается плоскость качания.
Билет №13. Кориолисово ускорение. Причина возникновения. Направление.
Простыми словами про силу Кориолиса:
При вращении диска, более далёкие от центра точки движутся с большей касательной скоростью, чем менее далёкие (группа чёрных стрелок вдоль радиуса). Если мы хотим переместить некоторое тело вдоль радиуса, так, чтобы оно оставалось на радиусе (синяя стрелка из положения «А» в положение «Б»), то нам придётся увеличить скорость тела, то есть, придать ему ускорение. Если наша система отсчета вращается вместе с диском, то мы ощутим, что тело «не хочет» оставаться на радиусе, а «норовит» уйти влево — это и есть сила Кориолиса.
На анимации демонстрируется движение шарика по поверхности вращающейся тарелки
Причины возникновения ускорения Кориолиса:
Для того, чтобы тело двигалось с кориолисовым ускорением, необходимо приложение силы к телу, равной F = ma, где a — кориолисово ускорение. Соответственно, тело действует по третьему закону Ньютона с силой противоположной направленности.
Направление:
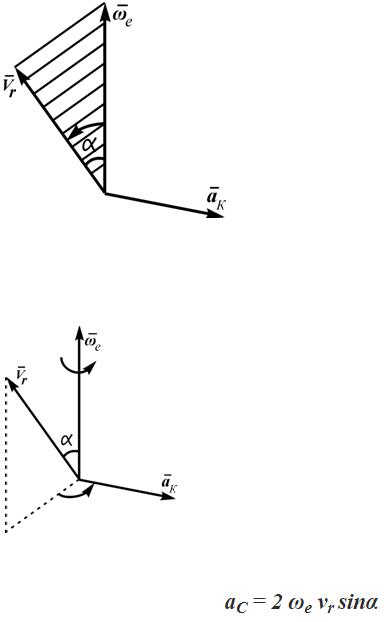
Направление ускорения Кориолиса определяется по правилу векторного произведения или по правилу Жуковского.
(смотри след. лист)
1. Правило векторного произведения
Согласно этому правилу вектор кориолисова ускорения перпендикулярен векторам ωe и Vr (или плоскости, проходящей через эти вектора, проведенные из одной точки). Направлен вектор aK так, что если смотреть ему навстречу, то кратчайший поворот вектора ωe до совмещения с вектором Vr происходит против хода часовой стрелки.
2. Правило Жуковского Для определения направления кориолисова ускорения нужно спроецировать вектор
относительной скорости в плоскость, перпендикулярную вектору переносной угловой скорости и полученную проекцию повернуть на в сторону переносного вращения.
Величина ускорения Кориолиса определяется выражением:
где α – угол между векторами ωee и νrr.
Билет №14. Принцип относительности и преобразования Галилея. Неинвариантность электромагнитных явлений относительно преобразований Галилея.
Краткая сводка
В основе классической̆механикилежитлежитположениеположениесуществованиисуществованиинекоторых некоторых абсолютных величин, единых для всех систем отсчета. К таким абсолютным величинам относятся время, расстояние, масса. Абсолютность означает, что длина и
масса некоторого конкретного предмета будет одной̆и тоймеханикиже во всехлежитинерциальныхположение о сущест системах отсчета. Ход часов также не изменяется от того, в какой̆инерциальномеханики лежит положени системе отсчета они расположены.
Кроме абсолютных величин, существуют относительные величины, зависящие от системы отсчета. К относительным величинам в первую очередь относится скорость. Относительными будут и все физические величины, зависящие от скорости, – импульс, кинетическая энергия и др.
Из абсолютного характера времени и расстояния, постулируемых в классической̆ механики механике, следуют простые классические формулы преобразования координат при переходе в расчетах от одной̆инерциальномеханики лежитсистемыположениек друго . Этиоформулысуществовании некоторы
называются преобразованиями Галилея.
Преобразования Галилея для некоторого частного случая
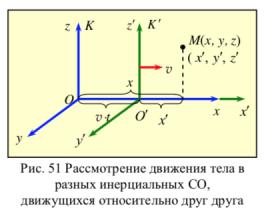
При рассмотрении двух инерциальных систем отсчета (например, системы K (x, y, z) и системы K’ (x’, y’, z’) ), часто принимают, что система K условно неподвижна, а система
K’ движется равномерно со скоростью v вдоль оси x (рис. 51). Конечно, можно было бы считать, что, наоборот, система K’ неподвижна, а система K движется, но это ничего не меняет в дальнейших выводах. Также принимается, что в
начальный̆моммеханикинт временилежитобе системыположение о существовании некоторых
совпадали. Тогда в момент времени t
координаты некоторой̆материальноханики лежточкитМ положениев о существовании некоторых
системе K’ будут связаны с координатами в системе K следующими соотношениями:
x'=x−vt
y'= y ; z'=z;t'=t
(1)
Эти соотношения называются прямыми преобразованиями Галилея. И, наоборот, координаты системы K будут связаны с координатами системы K’:
x=x'+vt
y= y' ; z=z ' ;t=t '
(2)

Эти соотношения и называются обратными преобразованиями Галилея. Из преобразований Галилея вытекает связь между скоростями движения некоторого конкретного тела в системах отсчета K и K’.
Для установления этой̆связимеханикинеобходимолежитпродиффереположениецироватьсуществованииуравнения (1) некоторых по времени:
dx'dt = dxdt =v
(3)
Можно ввести следующие обозначения:Скорость материальной̆точкимеханики лежит положе относительно системы отсчета K:
dxdt =u
(4)
Скорость этой же материальной̆точкимеханикиот оситележитьно системыположениеотсчетаоK’:существовании нек
dx'dt =u
(5)
Переносная скорость (скорость одной̆системымеханикиотсчеталежитпо отношениюположениек друго существовании) – v . нек Тогда уравнение (3) перепишется в виде:
u' =u −v
или
u =u' +v
(6)
Эти уравнения выражают собой̆законмеханикисложениялежитскоростеположениев классическосуществовании нек механике. Взяв еще раз производную по времени в соотношении (3), получим:
d2 x ' = d2 x dt2 dt2
(7)
Ускорение материальной̆точкимеханикив системележитотсчетаположениеK’: о существовании некоторы
d2 x2 ' =a' dt
(8)
Ускорение этой̆жемеханматериальноки лежитточкиположв системениеотсчетасуществованииK: некоторых
d2 x =a dt2
(9)
Сопоставляя между собой̆последниемеханикиуравненлежитя, мположениежно заметить,о существованиичто ускорения некотор в инерциальных системах отсчета одинаковы, т.е. a’ = a. II закон Ньютона в обеих
системах имеет вид:
F =ma F ' =m' a
Так как масса считается абсолютной̆величиномеханики(m'=лежитm), то Fположение' =F' . Такимо существовани
образом, уравнения движения конкретного тела (законы Ньютона) одинаковы во всех инерциальных системах отсчета, или они инвариантны относительно преобразований Галилея. Это и есть классический̆принципмеханикиотносительностилежит положениеГалилеяо существовании. Этот некот
принцип можно сформулировать и по-другому:
Никакими механическими опытами, выполненными в любой̆инерциальномеханики лежит положение системе, нельзя решить, двигается эта система или покоится.
Историческая справка
В середине ХIХ в. были разработаны методы, позволившие достаточно точно измерить скорость света. Оказалось, что в вакууме она составляет с = 3 * 108 м/с.
Возникает вопрос, к какой̆системемеханикиотсчеталежитотноситсяположениедан ое значениео существкорости?ванииВедьнекоторых говорить о скорости без указания системы отсчета бессмысленно. Из классического закона сложения скоростей̆следует,механикичто в лежитразных системахположениеотсчетасуществоскорос ь ветаании некоторых
должна быть различной̆. Поэтомумеханикизмеренноележит значениеполож ниескоростисуществованиисвета должно некоторых относиться лишь к одной̆какомеханики-то системележитотсчета,положениенапример,связанносуществованиисточникомнекоторых света.
Первый̆опытмеханикипо измерениюлежитскорпостиложениесвета водвижущейсясуществованиисистеме отсчетанекоторыхбыл поставлен Майкельсоном в 1881 г. Затем аналогичные эксперименты проводились другими учеными, причем точность измерений все время возрастала. Все эти опыты
дали отрицательный̆результатмеханики. Оказалось,лежит чтоположениево всех инерциальныхо существованиисистемах некоторых отсчета, независимо от величины и направления относительной̆ихмеханикискорости лежит положение движения, скорость света (в вакууме) одинакова и равна с = 3 *108 м/с.
Этот результат показывает, что классический̆законзаконсложениясложения скоростей̆имеетзаконграничсложениянную область применения. Он, в частности, непригоден для описания явлений, связанных с распространением света. Но классический̆законмеханикисложениялежитскоростеположениеявляется следствиемо существованиииз преобразованийнекоторых Галилея, следовательно, и они имеют ограниченную область применения.
Итак, преобразования Галилея оказались в противоречии с экспериментальным результатом – постоянства скорости света в инерциальных системах отсчета.
Приблизительно в это же время (в конце ХIХ в.) оказалось также, что преобразования Галилея не согласуются и с некоторыми теоретическими результатами. В это время Максвеллом была создана теория электромагнитного поля, написаны уравнения электродинамики (уравнения Максвелла). Оказалось, что если
преобразовать эти уравнения с помощью преобразований Галилея, то эти уравнения изменяются.
Следовательно, мы получаем, что электромагнитные явления неинвариантны относительно преобразований Галилея.
