Литература и лекции / Opredelenia

Определения:

1. Определение возрастания и убывания функции

2. Определение локального экстремума функции

3. Определение n-й производной функции

4. Определение выпуклости функции классическое

5. Определение выпуклости функции альтернативное

6. Определение точки перегиба функции.

7.Определение первообразной функции. Определение неопределённого интеграла.

●f: R -> R, F: R -> R; Функция F(х) есть первообразная функции f(x), если F’(x) = f(x).

●f: R->R; Множество всех первообразных функции f(x) есть

неопределенный интеграл функции f(x).

8.Определение дробно рациональной функции. Определение правильной и неправильной дробно рациональной функции.

Функция, представленная отношением двух полиномов

называется дробно рациональной функцией, или рациональной дробью. Если n > m, то дробь называется правильной.

Если n < = m, то дробь называется неправильной.

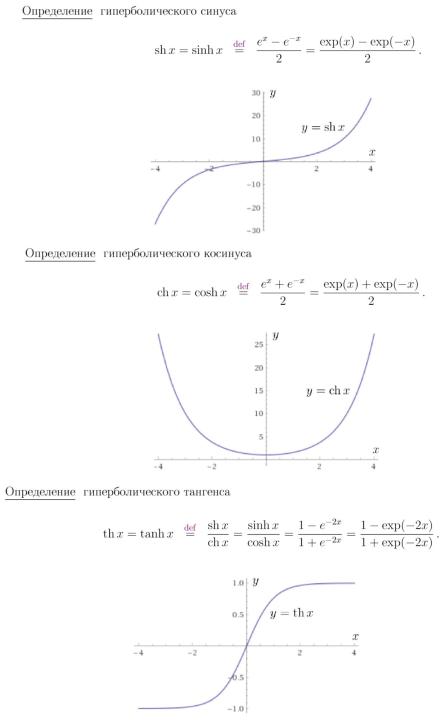
9. Определение гиперболической функции.

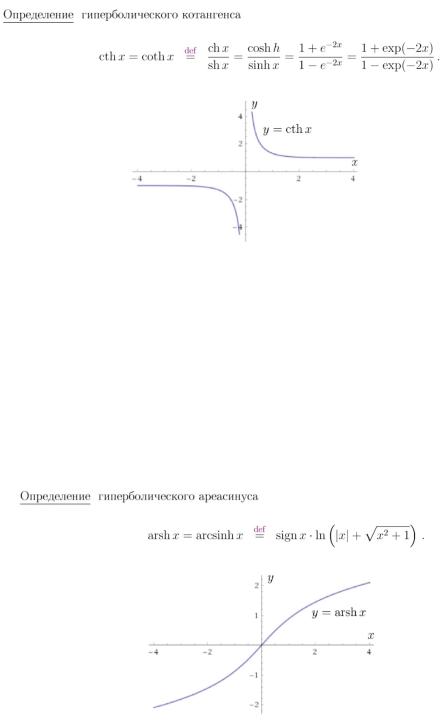
10. Определение обратных гиперболических функций.

11. Определённый интеграл

Набор точек {xi}i = 0, 1, 2,..,n , таких, что a = x0 < x1 < x2 < ... < xn = b , принято называть разбиением (или дроблением) промежутка [a, b] .

Число xi принято называть i -м узлом разбиения.

Число r = max(xi − xi−1) принято называть рангом разбиения.

Набор точек {ξi}i=1,2,...,n , таких, что xi−1 ≤ ξi ≤ xi , к сожалению, названия в литературе не удостоился.

Пусть f : [a, b] → .

n

Величину ∑ f (ξi) · (xi − xi−1) принято называть интегральной суммой.

i=1

Если существует и конечен предел интегральной суммы

n

lim ∑ f (ξi) · (xi − xi−1) ,

r→0 i=1

и этот предел не зависит от способа расстановки узлов xi на промежутке [a, b] и от выбора места для точек [xi−1, xi] , то принято говорить, что функция f (x) на промежутке

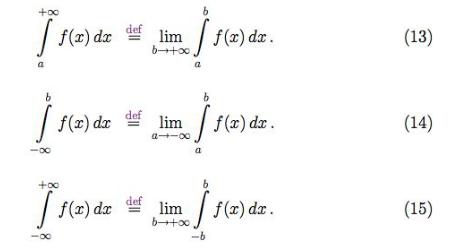
12. Геометрический смысл определённого интеграла. Определение подграфика функции.

Определение подграфика функции:

Пусть f : [a, b] → . Пусть f (x) ≥ 0, x [a, b].

Часть плоскости в декартовой прямоугольной системе координат xOy, ограниченная прямой y = 0 (снизу), прямой x = a (слева), прямой x = b (справа), и графиком функции y = f (x) (сверху), называется криволинейной трапецией, или подграфиком функции

f (x) на промежутке [a, b].

Геометрический смысл определённого интеграла:

●интегральная сумма примерно равна площади подграфика f(x) на [a, b];

●интеграл точно равен площади этого подграфика

Пытливый читатель скажет: "А всё-таки в последнем, фиолетовом пункте, что-то не так".

Безразличный читатель ответит: "А мне это глубоко фиолетово".

13. Определение несобственного интеграла 1 рода. Сходимость

Несобственный интеграл 1-го рода - это интеграл по промежутку бесконечно большой длины.

Если предел в (13) или в (14) существует и конечен, то принято говорить, что соответствующий несобственный интеграл сходится.

Если предел в (15) существует и конечен, то принято говорить, что несобственный

+∞

интеграл ∫ f (x)dx сходится в смысле Коши.

−∞

Если предел бесконечен либо не существует, то несобственный интеграл расходится.

14. Определение несобственного интеграла 2 рода. Сходимость

Несобственный интеграл 2-го рода - это интеграл по конечному промежутку, на одном из концов которого подынтегральная функция терпит разрыв второго рода.

15. Определение числового ряда и его сходимости

Числовой ряд - это совокупность двух последовательностей:

●основной последовательности чисел {an}n N ;

●вспомогательной последовательности {Sn}n N частичных сумм, содержащих элементы основной последовательности:

S1 = a1, S2 = a1 + a2, S3 = a1 + a2 + a3, ... , Sk = a1 + a2 + ... + ak, ... .

+∞

Обозначение: ∑ an.

n=1

Если существует и конечен предел lim Sk = S , принято говорить, что числовой ряд

k→+∞

сходится, а число S есть сумма ряда.

+∞

Если ряд сходится, и S есть сумма ряда, то принято писать ∑ an = S .

n=1

Если предел lim Sk бесконечен либо не существует, принято говорить, что числовой

k→+∞

ряд расходится.

+∞

16. Определение знакопеременного числового ряда. Определение знакочередующегося числового ряда.

Знакопеременными принято называть числовые ряды, слагаемые которых могут быть как положительными, так и отрицательными. Нулевые слагаемые тоже допускаются.

17.Определение абсолютной и условной сходимости.

●Знакопеременный числовой ряд абсолютно сходится,

если сходится знакопостоянный числовой ряд .

●Если знакопеременный числовой ряд сходится, а числовой ряд расходится, то принято говорить, что ряд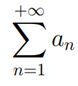

условно сходится.

18.Определение функционального ряда и его области сходимости.