
ПЭ5
.docxМинистерство науки и высшего образования Российской Федерации Федеральное государственное бюджетное образовательное учреждение
высшего образования
«ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ» (ТУСУР)
Кафедра комплексной информационной безопасности электронно-вычислительных систем (КИБЭВС)
ПОЛНЫЙ ФАКТОРНЫЙ ЭКСПЕРИМЕНТ
Отчет по лабораторной работе №5
по дисциплине «Планирование эксперимента»
Выполнил:
Студент гр.739-1
________Климанов М.Д.
22.12.2021
Проверил:
Доцент кафедры КИБЭВС
__________Шабля Ю.В.
22.12.2021
Томск 2021
1 Введение
Цель работы: изучение методики планирования и обработки результатов активного эксперимента на примере полного факторного эксперимента.
2 Ход работы
Данная лабораторная работа заключается в реализации решения 9-ой и 10-ой практических работ.
Программой, с помощью которой производились вычисления, стала Microsoft Excel.
Сведения варианта задания представлены в таблицах 2.1-2.4.
Таблица 2.1 – Информация о значениях факторов, влияющих на выходной параметр y

Таблица 2.2 – Матрица планирования

Таблица 2.3 – Результаты параллельных опытов

Таблица 2.4 – Рандомизация каждой серии параллельных опытов

Для дальнейшего решения были получены промежуточные значения и матрица планирования, представленные в таблице 2.5.
Таблица 2.5 – Промежуточные вычисления
№ |
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
-1 |
-1 |
-1 |
1 |
1 |
1 |
-1 |
-5,68 |
-5,29 |
-6,77 |
2 |
1 |
1 |
-1 |
-1 |
-1 |
-1 |
1 |
1 |
-12,52 |
-11,30 |
-16,21 |
3 |
1 |
-1 |
1 |
-1 |
-1 |
1 |
-1 |
1 |
-8,85 |
-4,84 |
-6,25 |
4 |
1 |
1 |
1 |
-1 |
1 |
-1 |
-1 |
-1 |
5,56 |
7,19 |
3,41 |
5 |
1 |
-1 |
-1 |
1 |
1 |
-1 |
-1 |
1 |
4,31 |
2,87 |
1,97 |
6 |
1 |
1 |
-1 |
1 |
-1 |
1 |
-1 |
-1 |
-9,42 |
-7,46 |
-10,47 |
7 |
1 |
-1 |
1 |
1 |
-1 |
-1 |
1 |
-1 |
2,70 |
5,09 |
3,74 |
8 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
10,51 |
10,15 |
12,22 |
Среднее
значение выходного параметра
 для каждой точки факторного пространства,
вычислялось по формуле:
для каждой точки факторного пространства,
вычислялось по формуле:
 ,
,
 – результат
измерения для j-ой
точки ФП в g-ой
серии измерений;
– результат
измерения для j-ой
точки ФП в g-ой
серии измерений;
M – количество серий параллельных опытов.
Результат вычислений по формуле среднего значения выходного параметра, представлен в таблице 2.6.
Таблица 2.6 – Результаты вычислений
|
|
|
|
-5,68 |
-5,29 |
-6,77 |
-5,91 |
-12,52 |
-11,30 |
-16,21 |
-13,34 |
-8,85 |
-4,84 |
-6,25 |
-6,65 |
5,56 |
7,19 |
3,41 |
5,39 |
4,31 |
2,87 |
1,97 |
3,05 |
-9,42 |
-7,46 |
-10,47 |
-9,12 |
2,70 |
5,09 |
3,74 |
3,84 |
10,51 |
10,15 |
12,22 |
10,96 |
Далее была произведена проверка воспроизводимости опытов по G -критерию Кохрена при уровне значимости α=0,05.
Формулы для критерия Кохрена:
 ;
;
 .
.
Значение
 было найдено при помощи таблицы и
параметров α=0,05,
было найдено при помощи таблицы и
параметров α=0,05,
 ,
,
 .
.

 ,
следовательно,
был сделан вывод, что дисперсия однородна.
,
следовательно,
был сделан вывод, что дисперсия однородна.
Результаты вычислений представлены на рисунке 2.1.

Рисунок 2.1 – Результаты вычислений
Затем
были найдены значения коэффициентов
уравнения регрессии
 .
Также выполнялась проверка значимости
коэффициентов уравнения регрессии по
критерию Стьюдента по формулам:
.
Также выполнялась проверка значимости
коэффициентов уравнения регрессии по
критерию Стьюдента по формулам:
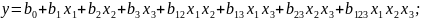





Результаты вычислений представлены на рисунке 2.2.

Рисунок 2.2 – Результаты вычислений
Линейная математическая модель в соответствии со значимыми коэффициентами:

Далее построена квазилинейная математическая модель в соответствии со значимыми коэффициентами:
 .
.
Была произведена проверка адекватности модели по критерию Фишера:


Было
найдено значение
 .
.

Результаты вычислений представлены в таблице 2.7.
Таблица 2.7 – Результаты вычислений
d |
|
|
а |
|
|
|
Вывод |
2 |
100,19 |
37,73 |
0,05 |
6,00 |
16,00 |
2,74 |
ММ не адекватна |
4 |
0,80 |
0,30 |
0,05 |
4,00 |
16,00 |
3,01 |
ММ адекватна |
На рисунке 2.3 изображены выводы математических моделей для натуральных значений факторов

Рисунок 2.3 – Вывод математических моделей
3 Заключение
В ходе лабораторной работы были изучены методики планирования и обработки результатов активного эксперимента на примере полного факторного эксперимента.





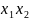








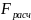
 =N-d
=N-d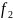 =N(M-1)
=N(M-1)