
Lessons In Industrial Instrumentation-16
.pdf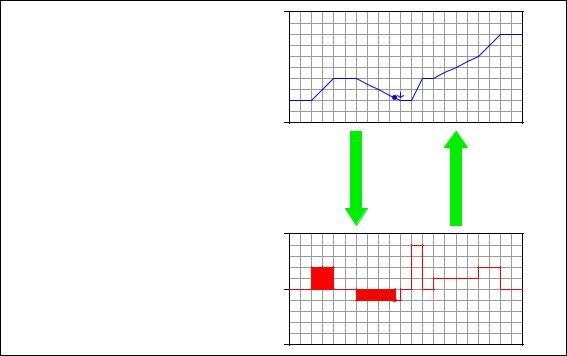
3034 |
APPENDIX A. FLIP-BOOK ANIMATIONS |
Note how the height increase of the volume graph directly relates to the area accumulated by the flow graph . . .
Max. |
V |
0 |
Flow rate (Q) is the derivative of volume with respect to time
Q =
dV dt
+Max.
Differentiation
Integration
Volume (V) is the integral of flow rate with respect to time
V = ò Q dt
Q 0
-Max.
A.4. DIFFERENTIATION AND INTEGRATION ANIMATED |
3035 |
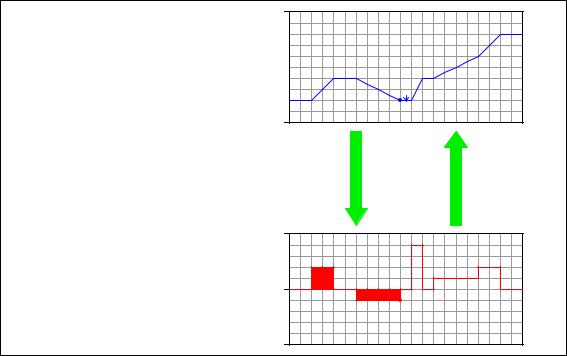
Note how the height increase of the volume graph directly relates to the area accumulated by the flow graph . . .
Max. |
V |
0 |
Flow rate (Q) is the derivative of volume with respect to time
Q =
dV dt
+Max.
Differentiation
Integration
Volume (V) is the integral of flow rate with respect to time
V = ò Q dt
Q 0
-Max.
3036 |
APPENDIX A. FLIP-BOOK ANIMATIONS |
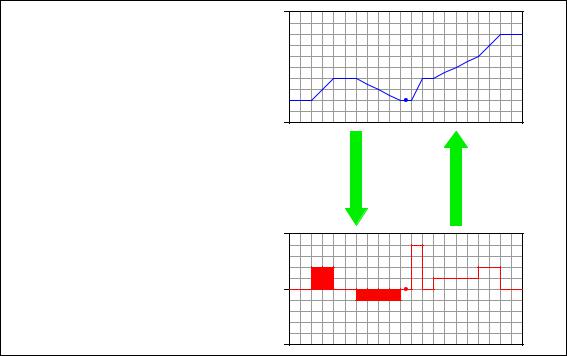
Note how the height increase of the volume graph directly relates to the area accumulated by the flow graph . . .
Max. |
V |
0 |
Flow rate (Q) is the derivative of volume with respect to time
Q =
dV dt
+Max.
Differentiation
Integration
Volume (V) is the integral of flow rate with respect to time
V = ò Q dt
Q 0
-Max.
A.4. DIFFERENTIATION AND INTEGRATION ANIMATED |
3037 |
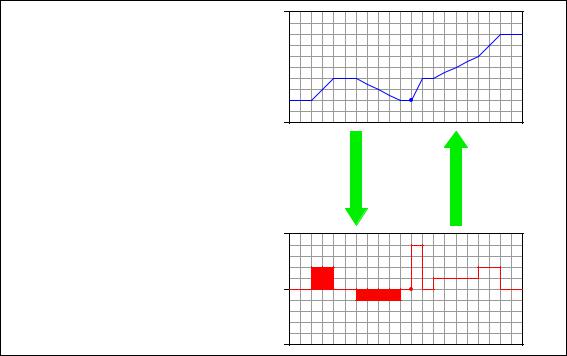
Note how the height increase of the volume graph directly relates to the area accumulated by the flow graph . . .
Max. |
V |
0 |
Flow rate (Q) is the derivative of volume with respect to time
Q =
dV dt
+Max.
Differentiation
Integration
Volume (V) is the integral of flow rate with respect to time
V = ò Q dt
Q 0
-Max.
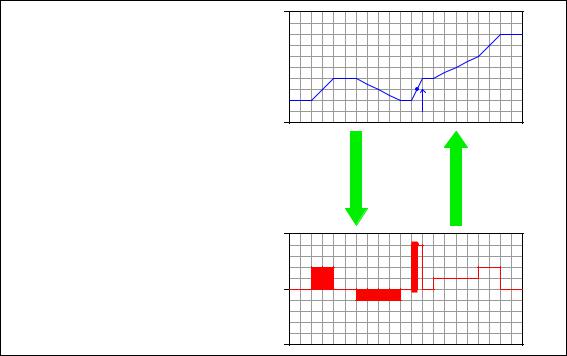
3038 |
APPENDIX A. FLIP-BOOK ANIMATIONS |
Note how the height increase of the volume graph directly relates to the area accumulated by the flow graph . . .
Max. |
V |
0 |
Flow rate (Q) is the derivative of volume with respect to time
Q =
dV dt
Differentiation
Integration
Volume (V) is the integral of flow rate with respect to time
V = ò Q dt
+Max. |
Q 0 |
-Max.
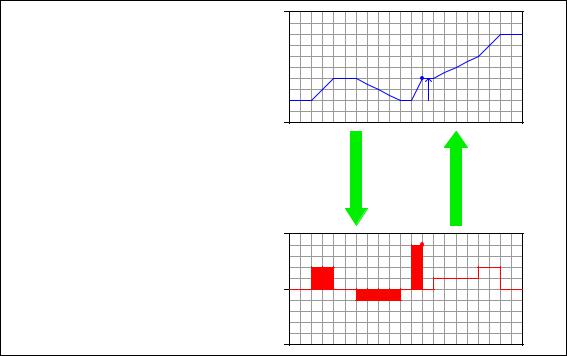
A.4. DIFFERENTIATION AND INTEGRATION ANIMATED |
3039 |
Note how the height increase of the volume graph directly relates to the area accumulated by the flow graph . . .
Max. |
V |
0 |
Flow rate (Q) is the derivative of volume with respect to time
Q =
dV dt
Differentiation
Integration
Volume (V) is the integral of flow rate with respect to time
V = ò Q dt
+Max. |
Q 0 |
-Max.
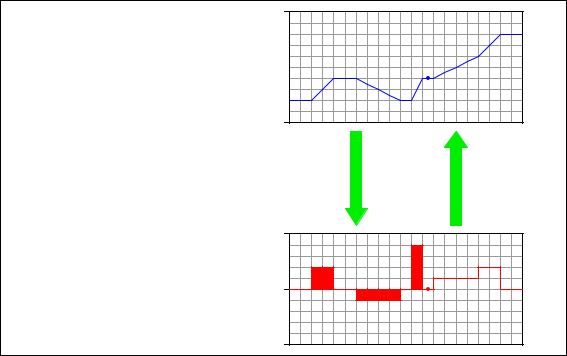
3040 |
APPENDIX A. FLIP-BOOK ANIMATIONS |
Note how the height increase of the volume graph directly relates to the area accumulated by the flow graph . . .
Max. |
V |
0 |
Flow rate (Q) is the derivative of volume with respect to time
Q =
dV dt
Differentiation
Integration
Volume (V) is the integral of flow rate with respect to time
V = ò Q dt
+Max. |
Q 0 |
-Max.
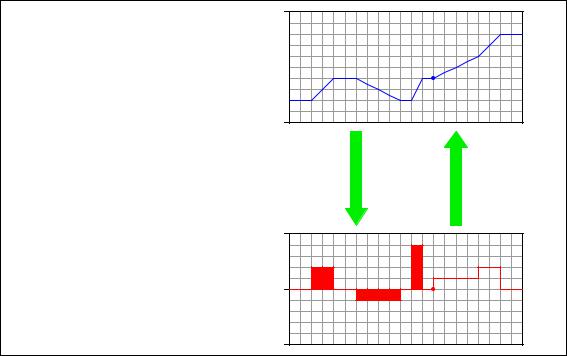
A.4. DIFFERENTIATION AND INTEGRATION ANIMATED |
3041 |
Note how the height increase of the volume graph directly relates to the area accumulated by the flow graph . . .
Max. |
V |
0 |
Flow rate (Q) is the derivative of volume with respect to time
Q =
dV dt
Differentiation
Integration
Volume (V) is the integral of flow rate with respect to time
V = ò Q dt
+Max. |
Q 0 |
-Max.
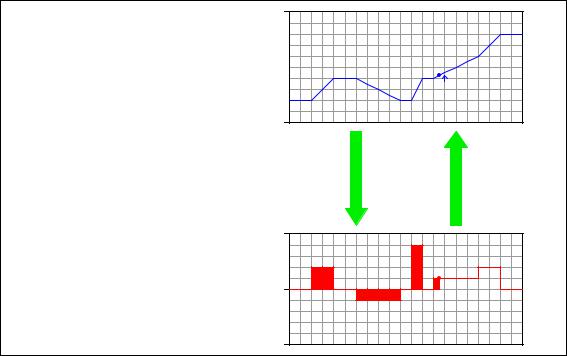
3042 |
APPENDIX A. FLIP-BOOK ANIMATIONS |
Note how the height increase of the volume graph directly relates to the area accumulated by the flow graph . . .
Max. |
V |
0 |
Flow rate (Q) is the derivative of volume with respect to time
Q =
dV dt
Differentiation
Integration
Volume (V) is the integral of flow rate with respect to time
V = ò Q dt
+Max. |
Q 0 |
-Max.
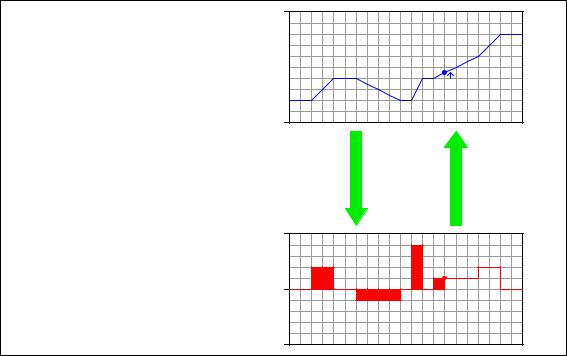
A.4. DIFFERENTIATION AND INTEGRATION ANIMATED |
3043 |
Note how the height increase of the volume graph directly relates to the area accumulated by the flow graph . . .
Max. |
V |
0 |
Flow rate (Q) is the derivative of volume with respect to time
Q =
dV dt
Differentiation
Integration
Volume (V) is the integral of flow rate with respect to time
V = ò Q dt
+Max. |
Q 0 |
-Max.
