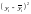2. Выборочное уравнение линейной регрессии Метод наименьших квадратов
При проведении современных клинических исследований обычно нет недостатка в информации: каждому пациенту соответствует целое множество различных клинических показателей и данных. В них могут быть завуалированы некоторые соотношения, основные черты которых и позволяют выявлять методы регрессионного анализа. При этом задача регрессионного анализа состоит в подборе упрощенной аппроксимации этой связи с помощью математической модели.
Регрессионный анализ имеет в своем распоряжении специальные процедуры проверки, является ли выбранная математическая модель адекватной для описания имеющихся данных.
Чаще всего регрессионный анализ используется для прогноза, то есть предсказания значений ряда зависимых переменных по известным значениям других переменных.
Выше указывалось, что результаты наблюдений, приведенные в двумерной выборке (табл. 8.7), можно представить в виде корреляционного поля точек (рис. 8.2), где каждая точка соответствует отдельным значениям x и y.
Таблица 8.7. Пример записи двумерной выборки
xi |
x1 |
x2 |
x3 |
x4 |
x5 |
yi |
|
|
|
|
|
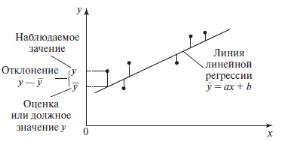
Рис. 8.2. Метод наименьших квадратов
В результате получается диаграмма рассеяния, позволяющая судить о форме и тесноте связи между варьирующими признаками. Довольно часто эта связь может быть аппроксимирована прямой линией (см. рис. 8.2).
Определение
Регрессия — это функция, позволяющая по величине одного признака X находить среднее ожидаемое (должное) значение другого признака Y, корреляционно связанного с X.
В линейной математической модели уравнение линейной регрессии имеет вид:
,
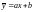где а и b — параметры линейной регрессии; а — коэффициент регрессии, показывающий, насколько в среднем величина одного признака Y изменяется при изменении на единицу меры другого признака X, корреляционно связанного с Y (чем больше α — угловой коэффициент прямой a = tgα, тем круче прямая, то есть быстрее изменяется Y); b — свободный член в уравнении, определяет при x = 0; — предсказанное (должное) значение Y для данного x при определенных значениях регрессионных параметров.
Параметры линейной регрессии определяют методом наименьших квадратов. Это способ подбора параметров регрессионной модели, согласно которому сумма квадратов отклонений вариант от линии регрессии должна быть минимальной:
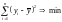. (8.3)
Необходимо подобрать параметры a и b так, чтобы точки, построенные по результатам наблюдений, находились как можно ближе к прямой линии регрессии.
Следовательно необходимо найти значения a и b, при которых функция F(a, b) будет иметь минимум:
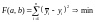
или
.
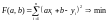Для отыскания минимума необходимо приравнять нулю частные производные:
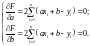
Выполнив преобразование, получаем систему двух линейных уравнений относительно a и b:
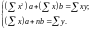
Решая эту систему, найдем значения a и b:
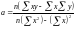; (8.4)
. (8.5)
Рассмотрим построение линии линейной регрессии на примере.
Пример 8.4. Исследовали зависимость между содержанием препарата в биологической ткани X и его концентрацией в крови пациента Y. Результаты наблюдений представлены в виде двумерной выборки (табл. 8.8).
Таблица 8.8. Исходные данные для примера 8.4
xi |
1,15 |
1,9 |
3,0 |
5,34 |
5,4 |
7,7 |
7,9 |
9,03 |
9,37 |
10,18 |
yi |
0,99 |
0,98 |
2,6 |
5,92 |
4,33 |
7,68 |
9,8 |
9,47 |
10,64 |
12,39 |
Решение. Результаты промежуточных вычислений представлены в табл. 8.9.
Таблица 8.9. Результаты промежуточных вычислений для примера 8.4
i |
xi |
yi |
|
xiyi |
|
|
|
1 |
1,15 |
0,99 |
1,32 |
1,14 |
0,27 |
0,72 |
0,52 |
2 |
1,9 |
0,98 |
3,61 |
1,86 |
1,21 |
–0,23 |
0,05 |
3 |
3,0 |
2,6 |
9,0 |
7,80 |
2,58 |
0,02 |
0,00 |
4 |
5,34 |
5,92 |
28,51 |
31,61 |
5,50 |
0,42 |
0,18 |
5 |
5,4 |
4,33 |
29,16 |
23,38 |
5,58 |
–1,25 |
1,56 |
6 |
7,7 |
7,68 |
59,29 |
59,14 |
8,45 |
–0,77 |
0,59 |
7 |
7,9 |
9,8 |
62,41 |
77,42 |
8,71 |
1,09 |
1,19 |
8 |
9,03 |
9,47 |
81,54 |
85,51 |
10,12 |
–0,65 |
0,42 |
9 |
9,37 |
10,64 |
87,79 |
99,69 |
10,54 |
0,1 |
0,01 |
10 |
10,18 |
12,39 |
103,63 |
126,13 |
11,56 |
0,83 |
0,69 |
|
60,97 |
64,8 |
466,26 |
513,68 |
|
0,28 |
5,21 |
Используя формулы (8.4) и (8.5), находим:
;
.
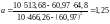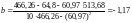Уравнение линейной регрессии имеет вид:
.
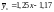Построим корреляционное поле точек (рис. 8.3).
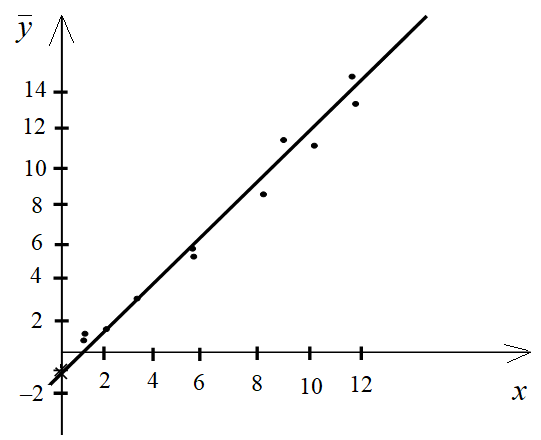
Рис. 8.3. График решения задачи
Рассчитаем должные величины:
при x = 0,
;
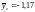при x = 10,
.
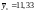Нанесем линию регрессии на график (см. рис. 8.3).
Из графика видно, что экспериментальные точки достаточно близко расположены к линии регрессии.