
lec01
.pdf
Кафедра Прикладной математики Института информационных технологий РТУ МИРЭА
Дисциплина
«Математическая логика
и теория алгоритмов»
2022-2023 уч.г.
Наполнение курса
Объем курса
16 лекционных и 8 практических занятий
Темы лекционных занятий
1.Элементы теории множеств. Булева алгебра
2.Булевы вектора и булевы функции
3.ДНФ, СДНФ, КНФ, СКНФ
4.Минимизация ДНФ
5.Метод Карно и метод Квайна
6.Двойственные функции
7.Функциональная полнота. Полные классы. Алгебра Жегалкина.
8.Замкнутые классы функций: монотонные, самодвойственные, сохраняющие const.
9.Теорема Поста
10.Исчисление высказываний
11.Исчисление предикатов. Основные положения. Кванторы
12.Нормальные формы. Доказательства
13.Конечные автоматы
14.Соединения и синтез автоматов
15.Машина Тьюринга
16.ЧРФ и НАМ
2
Тематика курса
Курс предназначен для ознакомления с основами булевой алгебры, полнотой систем булевых функций, минимизации нормальных форм, некоторыми приложениями булевой алгебры. Изучается формальная система классической логики 1 порядка и исследуются вопросы полноты и непротиворечивости.
В результате курса реализуются следующие компетенции:
1.Получение теоретических знаний о формальных системах 1 порядка.
2.Знание связей аппарата математической логики с основными математическими науками. А именно, общность всех структур математических наук, в том числе, и в методах доказательства теорем.
3.Владение алгоритмом распознавания тавтологий в логике высказываний.
4.Умение строить формальные доказательства и выводы в исчислении предикатов.
5.Формирование представлений о проблемах оснований математики и роли математической логики и теории алгоритмов в решении этих проблем.
3

Лекция 1.
Элементы теории множеств. Булева алгебра.
1.1.Элементы теории множеств.
1.2.Булева алгебра.

Часть 1.
Элементы теории множеств.
Что такое множество?
Квазиопределение. Под множеством U будем понимать любое собрание определенных и различимых между собою объектов, мыслимое как единое целое.
Формально U – множество из конечного (или бесконечного) числа элементов: U = {a1, a2, … an}.
Если Y = {x A(x)}, то A(x) называется характеристическим свойством множества Y.
Способы задания множества: перечисление или задание A(x) n = |U| - мощность множества U.
Рассмотрим всевозможные подмножества множества U. Обозначим его как Р(U) – множество всех подмножеств (множество-степень U), включающее Ø – пустое множество и само множество U.
Задание множества.
{3, 5, 6}
{а, б, в … я}
N, R, Z и др.
6
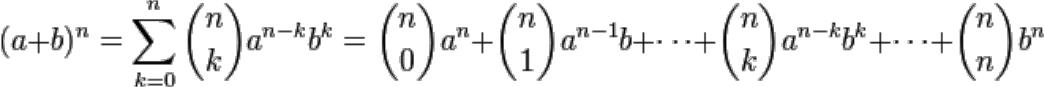
Теорема о количестве подмножеств.
Теорема 1.1. Множество U из n элементов будет содержать 2n подмножеств согласования.
1)Сосчитаем количество подмножеств – пустое подмножество плюс подмножества из одного элемента (их n), плюс подмножества из двух элементов множества и т.д. Имеем (1+1)n по формуле бинома Ньютона: (1+1) n
2)Запишем множество U = {a1, a2, … an}. Смотрим на a1. Имеется две возможности – взять его или нет? Далее смотрим на a2 – опять две возможности. Всего: 2 · 2 · … · 2 = 2n возможностей.
7
Кризис наивной теории множеств.
В математике рассматривается одна теория — теория множеств, которая длительное
время претендовала на выразимость в ней всех математических понятий. Рассмотрим существование множества всех множеств (парадокс Рассела).
Одна из аксиом «наивной» теории множеств: если X — множество, то для любого условия A имеем {x x X и A(x)} — также множество.
Выберем теперь свойство A следующим образом: A(x) — «x не содержит себя в качестве элементов». Примером множества, обладающего свойством A, служит, например, любое конечное множество.
Если обозначить через U универсум — множество всех множеств, то тогда можно определить множество Y = {x x U и A(x)} = {x x U и x x}.
Спрашивается, выполняется ли Y Y или Y Y ?
Любое из этих двух предположений влечет противоположное утверждение: по способу определения множества Y – его элемент обладает свойством A(x), т.е. Y Y. Но если это верно, то множество Y должно содержать Y как элемент => Y Y.
Обратно: если (элемент) Y Y (множеству), значит Y обладает характеристическим
свойством A(x), т.е. Y Y.
8
Парадокс Греллинга-Нельсона.
множество прилагательных.
Gm = {x A(x)},
где A(x) – гомологичность: соответствие своему смыслу. Примеры: русское – русское, трёхсложный – трёхсложное.
Большинство прилагательных своему смыслу не соответствуют, т.е. множество
Gt = {x B(x)},
где B(x) – гетерологичность: несоответствие своему смыслу A(x) не выполняется.
Примеры: сладкий – не сладкое, красный – не красное.
Прилагательное гетерологичное к каким относится: гомологичным или гетерологичным?
9

Алгебра подмножеств.
М – произвольное множество.
ВМ задана бинарная алгебраическая операция, если указан закон, по которому каждой паре элементов множества М сопоставляется некоторый третий элемент из М.
ВМ задана унарная алгебраическая операция, если указан закон, по которому каждому элементу множества М сопоставляется некоторый элемент из М.
Если М ≡ , то пример бинарной операции:
1) a + b; ab; .
Пример унарной операции:
a → – a
a → . |
10 |
|
