
Лекция_КЛАССИЧЕСКИЙ МЕТОД АНАЛИЗА ПЕРЕХОДНЫХ КОЛЕБАНИЙ В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ
.pdf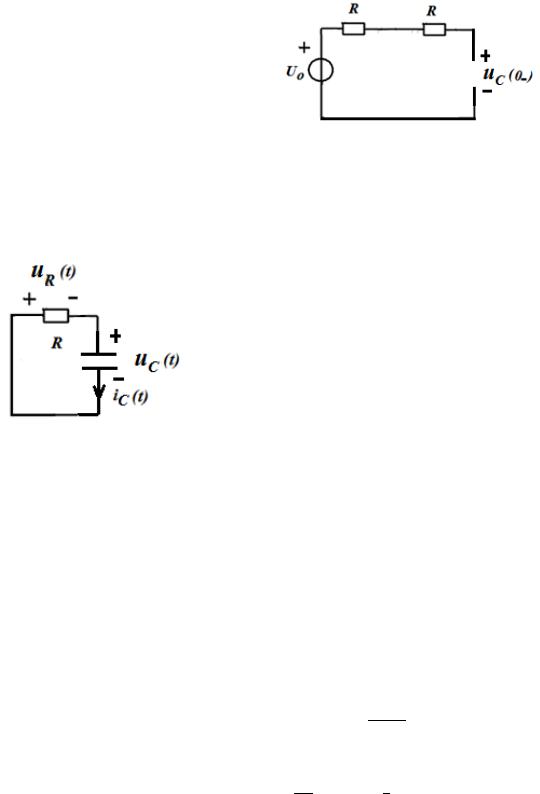
В этом режиме ток на емкости |
|
|||
( ) равен нулю, что эквивалентно |
|
|||
|
|
|
|
|
размыканию зажимов емкости. Тогда |
|
|||
схема приобретает вид, показанный |
|
|||
на рис. 1.13. |
|
|
|
|
Найдем напряжение на зажимах |
|
|||
емкости: |
|
|
|
Рис. 1.13. Схема RC-контура в |
|
(0 |
− |
) = . |
режиме постоянного тока при = 0− |
|
|
0 |
|
|
Для цепи после коммутации ( ≥ 0), представленной на рис. 1.14, которая образуется из исходной цепи после замыкания ключа, составим уравнение по второму закону Кирхгофа:
Рис. 1.14. Схема RC-контура после коммутации( ≥ 0)
|
|
|
( ) + ( ) = 0, |
|||||||
|
|
|
|
|
|
|
|
( ) |
|
|
где |
|
( ) = |
|
( ) ∙ ; |
|
|
( ) = |
. |
||
|
||||||||||
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|||
Подставим эти выражения в уравнение по второму закону Кирхгофа и получим дифференциальное уравнение относительно напряжения
( ):
|
( ) |
|
|
|
||
∙ |
|
|
+ |
|
( ) = 0. |
|
|
|
|||||
|
|
|
||||
|
|
|
|
|||
Полученное уравнение является линейным однородным дифференциальным уравнением первого порядка, поскольку в цепи один реактивный элемент – емкость.
Решение данного однородного уравнения будем искать в виде свободной составляющей (вынужденная составляющая равна нулю). Свободная составляющая, а, следовательно, и полное решение имеет вид:
( ) = св( ) = 1е 1 .
Показатель степени экспоненты 1 является корнем характеристического уравнения:
1∙ ∙ + 1 = 0, т. е. 1 = − ∙ .
Корень характеристического уравнения является вещественным отрицательным числом.
В результате, ( ) = св( ) = 1е− 1∙ = 1 − , где = ∙ имеет размерность времени и называется постоянной времени RC-контура.
Из начальных условий находим постоянную интегрирования 1:
(0−) = 1е0 = 1 = 0.
Окончательное решение дифференциального уравнения будет иметь следующий вид:
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||
|
|
|
( ) = |
|
( ) = е− |
|
|
= − . |
|
|
|||||||||||
|
|
св |
∙ |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
0 |
|
|
|
|
||||
Определим ток |
|
( ) через напряжение |
|
( ): |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
( ) |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
( ) = |
|
|
|
= − |
|
0 |
− . |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Величины 1 |
и будут зависеть от структуры цепи и ее параметров. |
||||||||||||||||||||
Если = , |
то ( ) = −1 |
= |
0 |
и |
|
( ) = − |
0 |
−1 = − |
0 |
. Таким |
|||||||||||
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∙ |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
образом, постоянная времени определяет время, за которое ток и напряжение на емкости в RC-контуре убывают по абсолютной величине в режиме свободных колебаний в ≈ 2,72 раз и составляют
|
|
( ) = |
0 |
≈ 0,37 |
и |
|
( ) = − |
0 |
|
≈ −0,37 |
0 |
. |
|
|
|
|
|||||||||||
|
|
|
|
0 |
|
|
∙ |
|
|
||||
|
|
|
|
|
|
|
|
|
|||||
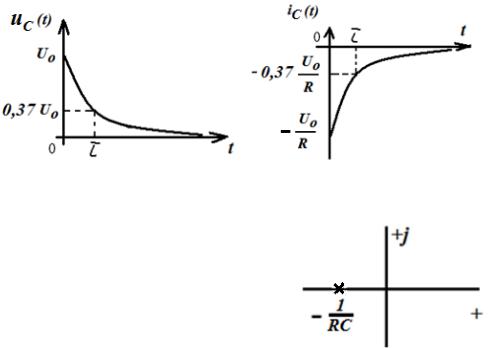
Графики |
полученных |
зависимостей ( ) |
(рис. 1.15, а) и ( ) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
(рис. 1.15, б) показывают, что абсолютные значения этих величин убывают по экспоненте со скоростью, которая определяется постоянной времени (как и для RL-контура).
а) |
|
б) |
Рис. 1.15. Графики зависимостей |
|
( ) (а) и ( ) (б) |
|
|
На рис. 1.16 показано расположение корня характеристического уравнения, который расположен в левой полуплоскости на ее вещественной отрицательной полуоси (как и для RL-контура).
Рис. 1.16. Расположение корня характеристического уравнения на комплексной плоскости
1.6. Переходные колебания в цепях с одним реактивным элементом при ступенчатом воздействии
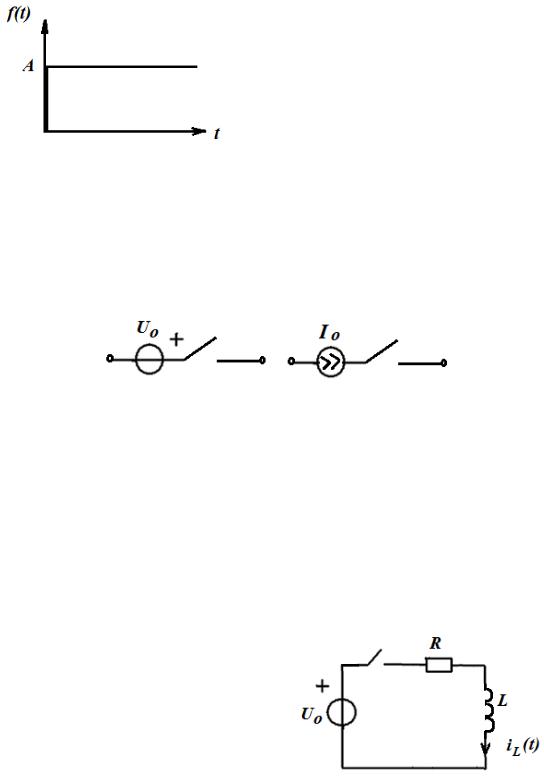
Ступенчатое воздействие напряжения или тока описывается функцией, представленной на рис. 1.17.
( ) = {0, |
при < 0; |
, |
при ≥ 0. |
Рис. 1.17. Ступенчатое воздействие
Ступенчатое воздействие напряжения (тока) называют перепадом или скачком напряжения (тока). Практически перепад напряжения (тока) соответствует включению в цепь источника постоянного напряжения (тока) и легко моделируется цепью из источника постоянного напряжения (тока) и ключа, который замыкается в момент = 0 (рис. 1.18).
Рис. 1.18. Цепи, моделирующие ступенчатое воздействие
1.6.1. Переходные колебания в последовательном RL-контуре при ступенчатом воздействии
Найдем законы изменения тока и напряжения в последовательном RL - контуре, если к его входу подведено напряжение в виде ступенчатого воздействия:
( ) = { 0, |
|
при < 0; |
|
0 |
0 |
, |
при ≥ 0. |
|
|||
Подобной задаче соответствует подключение к контуру источника постоянного напряжения 0( ) = 0
вцепи, представленной на рис. 1.19,
вмомент замыкания ключа = 0.
Рис. 1.19. Схема RL-контура
Определим начальные условия. До коммутации токи и напряжения в RL-цепи были равны нулю, т.е. цепь находилась в состоянии покоя.
Поэтому (0−) = (0+) = 0, т.е. имеем нулевые начальные условия.
Для t в цепи после коммутации (рис. 1.20) запишем уравнение по второму закону Кирхгофа.
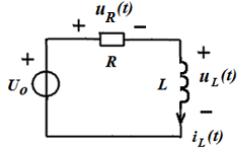
Рис. 1.20. Схема RL-контура после коммутации (t )
( ) + ( ) = 0( ),
где ( ) и ( ) – напряжения на |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
резистивном |
сопротивлении |
и |
||||||||
индуктивности. |
Выразим |
|
эти |
|||||||
напряжения |
через |
|
ток |
( ) |
в |
|||||
|
|
|
|
|
|
|
|
|
|
|
контуре, |
|
используя известные |
||||||||
соотношения |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
( ) |
|
|
( ) = |
|
( ) |
∙ ; |
|
|
( ) = |
|
|
|
. |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
Тогда получим следующее уравнение:
|
|
|
( ) |
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
( ) ∙ = |
0 |
( ) = . |
(1.11) |
||
|
|
|
|||||||||
|
|
|
|
|
|
|
0 |
|
|||
|
|
|
|
|
|
|
|
|
|
||
Полученное |
уравнение |
является |
линейным |
дифференциальным |
|||||||
уравнением первого порядка, что соответствует цепи с одним реактивным элементом. Дифференциальное уравнение имеет постоянные коэффициенты и является неоднородным (правая часть отлична от нуля), т.к. в цепи после коммутации имеется источник.
Решение дифференциального уравнения в соответствии с изложенным выше порядком, будем искать в виде суммы (1.5)
( ) = св( ) + вын( ),
где св( ) – общее решение однородного уравнения с правой частью равной нулю, а вын( ) = уст( ) – частное решение уравнения (1.11), которое определяется как установившееся значение искомой переменной в цепи после коммутации.
Для определения св( ) запишем характеристическое уравнение, соответствующее полученному дифференциальному. Оно будет иметь вид:
+ = 0,
его корень будет равен: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 = − |
|
= − |
1 |
. |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|||||
В соответствии с этим свободная составляющая |
|
|
|
|
|||||||||
|
( ) = е 1 |
= |
е− |
|
= |
− |
|
, |
|
||||
|
|
(1.12) |
|||||||||||
св |
1 |
1 |
|
1 |
|
|
|
|
|||||
где – постоянная интегрирования; = |
|
|
– имеет размерность времени и |
||||||||||
1 |
|
|
|
называется постоянной времени RL-цепи. |
|
Необходимо отметить, что в цепи с одним реактивным элементом |
|
дифференциальное уравнение для искомой переменной будет первого порядка как для свободных, так и для переходных колебаний. Постоянные
будут зависеть от структуры цепи и ее параметров.
Вынужденную составляющую вын( ) будем определять как установившееся значение тока в цепи. В установившемся режиме при t в цепи установится режим постоянного тока, при котором напряжение
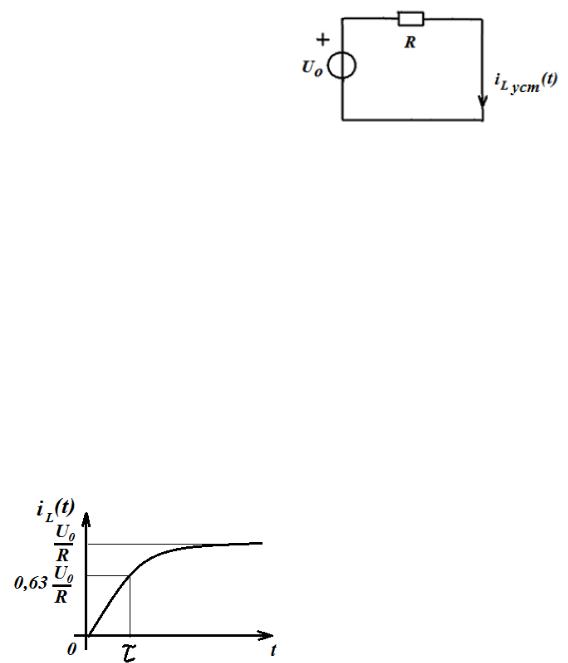
индуктивности тождественно, т.е. для любого момента времени, равно нулю
(согласно соотношению ( ) =
Поэтому в установившемся режиме постоянного тока индуктивность можно представить коротким замыканием, а всю схему в виде, представленном на рис. 1.21.
В данной схеме определяем
|
( ) |
|
|
|
|
|
|
|
= 0 |
при |
|
( ) = const). |
|
|
||||||
|
|
|
||||
|
|
|
|
|||
Рис. 1.21. Схема RL-контура в режиме постоянного тока при t
|
|
|
( ) = |
уст |
( ) = |
0 |
. |
(1.13) |
||||
|
|
|
||||||||||
|
|
вын |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||
|
Полный переходный ток, согласно 1.11–1.13 равен |
|
||||||||||
|
|
( ) |
− |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
= е |
|
+ |
|
. |
|
|
(1.14) |
|||
|
|
|
|
|
|
|||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Постоянную интегрирования 1 |
определяем из начальных условий |
||||||||||
(0 |
+ |
) = 0. После коммутации ток в цепи описывается выражением (1.14). |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Полагая в нем = 0 и приравнивая полученное выражение известному
начальному значению, получим (0 |
+ |
) |
= |
+ |
0 |
= 0. |
Отсюда |
|
= − |
0 |
. |
|||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Окончательное решение (1.14) принимает вид: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
( ) = |
0 |
|
− |
0 |
е− |
|
|
= |
0 |
|
(1 − е− |
|
). |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
(1.15) |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
График зависимости тока от времени представлен на рис. 1.22. |
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
До коммутации |
|
ток |
в |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
индуктивности равен нулю и с |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
этого |
же |
|
|
значения |
начинает |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
изменяться |
|
|
после коммутации. |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
При = ток нарастает до 0.63 от |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
установившегося значения |
|
0 |
, |
а |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
при = 4 достигает значения |
||||||||||||||||||||||
|
|
Рис. 1.22. График зависимости тока |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
0.98 ∙ |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
на индуктивности от времени |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
По истечении времени = (4 − 5) переходный процесс практически |
||||||||||||||||||||||||||||||||
завершается и в цепи устанавливается постоянный ток |
уст |
( ) = |
0 |
. |
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Напряжения на индуктивности можно определить по найденному току |
||||||||||||||||||||||||||||||||
|
|
( ) с использованием известного соотношения: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
( ) = |
|
|
|
|
= е− . |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
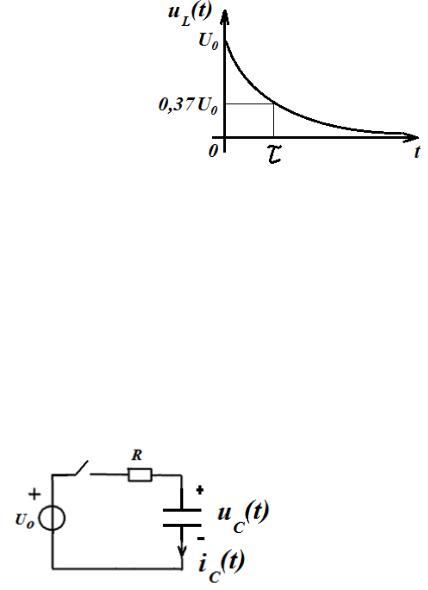
График ( ) приведен на рис. 1.23. Напряжение на индуктивности( ) пропорционально производной от тока и в первый момент после коммутации напряжение на индуктивности равно U0, т.е. изменяется скачком, т.к. до коммутации оно равнялось нулю.
Это не противоречит законам коммутации, которые выполняются только для токов в индуктивностях и для напряжений на емкостях.
Рис. 1.23. График зависимости напряжения на индуктивности от времени
1.6.2. Переходные колебания в последовательном RC-контуре при ступенчатом воздействии
Найдем законы изменения тока и напряжения в последовательном RC - контуре, если к его входу подведено напряжение в виде ступенчатого воздействия:
( ) = { 0, |
|
при < 0; |
|
0 |
0 |
, |
при ≥ 0. |
|
|||
Подобной задаче соответствует подключение к контуру источника постоянного напряжения 0( ) = 0 в цепи, представленной на рис. 1.24, в момент замыкания ключа = 0.
Определим начальные условия. До коммутации токи и напряжения в RC-цепи были равны нулю, т.е. цепь находилась в состоянии покоя. Поэтому
(0−) = (0+) = 0, т.е. имеем
нулевые начальные условия.
Рис. 1.24. Схема RC-контура
Для t в цепи после коммутации (рис. 1.25) запишем уравнение по второму закону Кирхгофа.
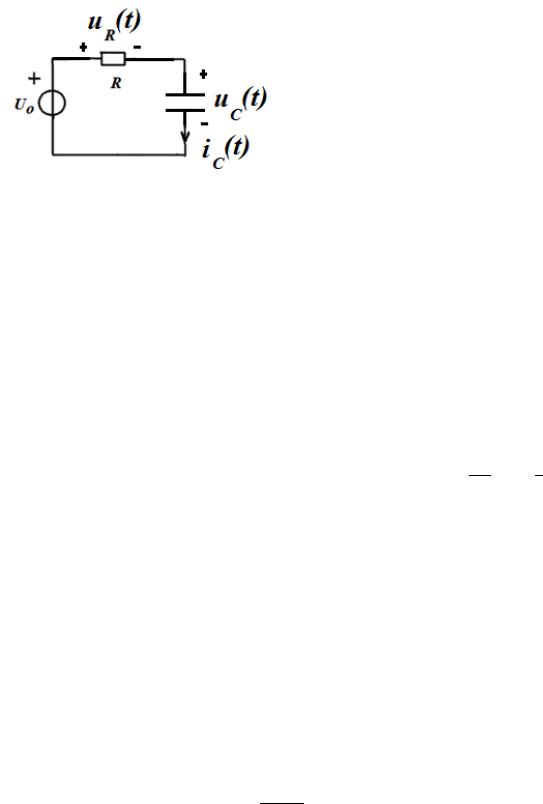
|
|
|
|
|
|
|
|
|
|
|
( ) + ( ) = ( ), |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
где |
|
( ) и |
|
( ) – напряжения на |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
резистивном |
|
сопротивлении и |
|||||||||
|
|
|
|
|
|
|
|
емкости. Выразим эти напряжения |
|||||||||||
|
|
|
|
|
|
|
|
через |
|
ток |
|
( ) |
|
в контуре, |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
используя известные соотношения |
|||||||||||
|
|
|
|
|
|
|
|
( ) = ( ) ∙ ; |
|
|
( ) = |
( ) |
. |
||||||
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Рис. 1.25. Схема RC-контура |
|
|
|
Тогда |
|
|
получим |
|
следующее |
||||||||||
после коммутации (t ) |
|
|
|
уравнение: |
|
|
|
|
|
|
|
||||||||
∙ |
( ) |
+ |
( ) = |
0 |
( ) = . |
|
|
|
|
(1.11) |
|||||||||
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение дифференциального уравнения в соответствии с изложенным |
|||||||||||||||||||
выше порядком, будем искать в виде суммы (1.5) |
|
|
|
|
|
|
|
||||||||||||
|
|
|
( ) = |
св |
( ) + |
|
|
( ), |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
вын |
|
|
|
|
|
|
|
|
||||
где св( ) – общее решение однородного уравнения с правой частью равной нулю, а вын( ) = уст( ) – частное решение уравнения (1.16), которое определяется как установившееся значение искомой переменной в цепи после коммутации.
Для определения св( ) запишем характеристическое уравнение, соответствующее полученному дифференциальному. Оно будет иметь вид:
∙ ∙ + 1 = 0, а его корень будет равен: 1 = − 1∙ = − 1. В соответствии с этим свободная составляющая
|
( ) = |
е 1 |
= |
е− |
1 |
= − |
|
, |
|
∙ |
|
(1.17) |
|||||||
св |
1 |
|
1 |
1 |
|
|
|
||
где 1 – постоянная интегрирования; = ∙ – имеет размерность времени и называется постоянной времени RC-цепи.
Необходимо отметить, что в цепи с одним реактивным элементом дифференциальное уравнение для искомой переменной будет первого порядка, и, следовательно, собственная составляющая будет иметь вид
(1.17). Постоянные 1 и будут зависеть от структуры цепи и ее параметров.
Вынужденную составляющую вын( ) будем определять как установившееся значение напряжения в цепи. В установившемся режиме при t в цепи установится режим постоянного тока, при котором ток емкости тождественно, т.е. для любого момента времени, равен нулю
(согласно соотношению ( ) = ( ) = 0 при ( ) = const).
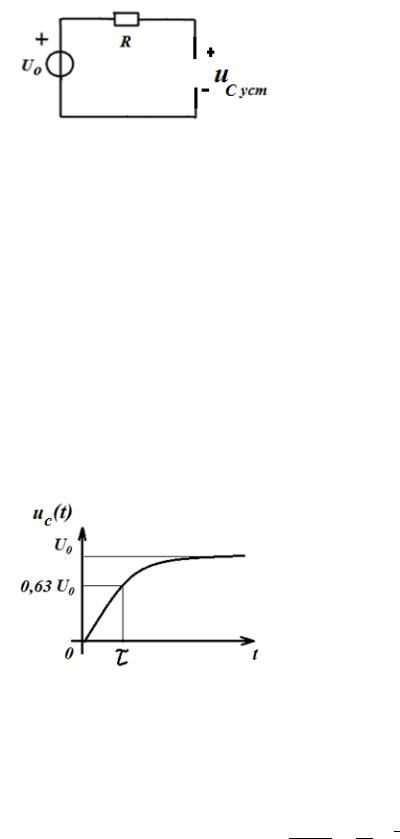
Поэтому в установившемся
|
|
|
|
|
|
|
|
|
режиме постоянного тока емкость |
|||||||||
|
|
|
|
|
|
|
|
|
представляет из себя обрыв цепи, |
|||||||||
|
|
|
|
|
|
|
|
|
и схему можно представить в виде |
|||||||||
|
|
|
|
|
|
|
|
|
рис. 1.26. |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
Из представленной схемы |
|||||||
Рис. 1.26. Схема RC-контура в режиме |
|
|
|
определяем |
|
|
|
|
||||||||||
|
|
постоянного тока при t |
|
|
|
|
|
|
|
|
вын |
( ) |
= |
( ) = . |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
уст |
0 |
|||
Полное напряжение на емкости равно |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
( ) = е− |
|
+ . |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
(1.18) |
|||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
0 |
|
|
|
|
|
|
Постоянную интегрирования 1 |
определяем из начальных условий |
|||||||||||||||||
(0 |
+ |
) = 0. После |
коммутации напряжение |
|
|
|
в |
цепи |
описывается |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
выражением (1.18). Полагая в нем |
= 0 |
и |
приравнивая |
полученное |
||||||||||||||
выражение известному начальному значению, получим |
|
|||||||||||||||||
|
|
|
(0 |
+ |
) = + |
= 0. |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
1 |
|
0 |
|
|
|
|
|
|
|
|
Отсюда 1 = − 0. Окончательное решение (1.18) принимает вид: |
||||||||||||||||||
|
|
|
( ) = − е− |
|
|
= |
(1 − е− |
|
). |
|
|
|||||||
|
|
|
|
|
(1.19) |
|||||||||||||
|
|
|
0 |
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
||
График зависимости напряжения на емкости от времени представлен на рис. 1.27.
Рис. 1.27. График зависимости напряжения на емкости от времени
До коммутации напряжение на емкости равно нулю и с этого же значения начинает изменяться
после коммутации. При = напряжение нарастает до 0.63 от установившегося значения 0, а при = 4 достигает значения
0.98 ∙ 0.
По истечении времени = (4 − 5) переходный процесс практически завершается и в цепи устанавливается постоянное напряжение
уст( ) = 0.
Ток ( ) можно определить по найденному напряжению ( ) с использованием известного соотношения:
( ) = ( ) = е− .
График ( )приведен на рис. 1.28.

Рис. 1.28. График зависимости тока на емкости от времени
Необходимо отметить, что до коммутации токи и напряжения в цепи были равны нулю. В момент коммутации напряжение на емкости остается нулевым, а ток скачком
изменяется до величины (0+) = , а затем постепенно спадает до нуля.
Скачок тока не противоречит законам коммутации, т.к. это не ток в индуктивности.
1.7.Расчет переходных колебаний в разветвленных цепях
содним реактивным элементом и источниками постоянного тока и напряжения
Расчет переходных колебаний в таких цепях можно произвести, используя общий порядок, изложенный в разделе 1.4, т.е. путем составления уравнений Кирхгофа и получения дифференциального уравнения. Очевидно, что при одном реактивном элементе в цепи порядок дифференциального уравнения будет первым. Другой способ решения рассматриваемой задачи – применение общей формулы, описывающей переходные токи и напряжения в цепи первого порядка, а именно:
|
A e p1t f ( ) A e |
t |
|
|
|
|
|
|
|
||
f(t) = f(∞) + |
|
, |
(1.20) |
||
|
1 |
1 |
|
|
|
где f(t) – переходный ток или напряжение в цепи; А1 – постоянная
интегрирования; – постоянная времени цепи; f(∞) = fвын = fуст – установившееся значение искомой переменной в цепи после коммутации, которое определяется при → ∞.
Постоянную интегрирования можно определить с помощью начального значения искомой переменной f(0+). Действительно, из (1.20)
имеем: f(0+) = f(∞) + А1, откуда А1 = f(0+) f(∞). Таким образом, в данном случае постоянная интегрирования равна разности между начальным и
установившимся (конечным) значениями искомой переменной. Решение (1.20) окончательно запишем в следующем виде:
|
e |
t |
|
|
f(t) = f(∞) + [ f (0 ) f ( )] |
|
. |
(1.21) |
|
Рассмотрим определение величин, входящих в (1.21).
1.Начальное значение f(0+) определяется из схемы для t = 0+, в которой заданы или определены независимые начальные условия uC(0+) или iL(0+). Для расчета могут быть использованы законы Кирхгофа или любые другие методы. В частности, по теореме замещения (компенсации) реактивный
элемент для рассматриваемого момента времени t = 0+ может быть заменен источником постоянного напряжения uC(0+) (если это емкость) или источником постоянного тока iL(0+) (если это индуктивность). В образованной таким образом резистивной цепи с источниками постоянного тока и напряжения могут быть определены начальные значения для всех токов и напряжений, в том числе и для искомой переменной.
2.Установившееся значение f(∞) = fвын = fуст определяется из схемы после коммутации в установившемся режиме постоянного тока при → ∞,
вкоторой реактивный элемент представляется либо коротким замыканием (индуктивность) либо обрывом (емкость).
3.Постоянная времени RC-цепи определяется по формуле = RЭC, а
для RL-цепи = L / RЭ, где RЭ – эквивалентное сопротивление, рассчитанное относительно зажимов реактивного элемента в пассивном двухполюснике, полученном из заданной цепи путем удаления источника напряжения (внешние зажимы которого замыкаются накоротко) или (и) источника тока (внешние зажимы которого размыкаются).
Далее рассмотрим примеры решения задач классическим методом:
Пример 1.7.1
Для цепи, представленной на рис. 1.29, определить переходный ток iL(t) путем составления и решения дифференциального уравнения.
Источник постоянного напряжения U0 подключается к разветвленной цепи с индуктивностью.
Начальные условия нулевые, т.е. (0+) = (0_) = 0.
Составим уравнения Кирхгофа. Линейно независимая система должна состоять в данном случае из трех уравнений (три неизвестных тока), причем одно уравнение составляем по первому закону Кирхгофа и два уравнения по второму закону Кирхгофа:
|
|
( ) = |
|
( ) + |
2 |
( ); |
|
|
||||
|
1 |
|
|
|
|
|
|
|
|
|||
|
|
( ) |
|
|
|
|
( ) |
|
|
|||
1( ) 1 |
+ |
|
|
= 0; |
|
|
|
|
= 2 |
( ) 2. |
||
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||
