
ХТП не гартман
.pdf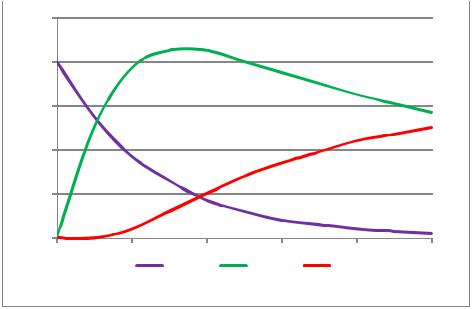
|
|
W1 k1 |
CA ; |
|
|
|
|||
|
W2 k2 |
CC2 ; |
|
|
|
||||
|
|
dCA |
=-k C |
; |
|
|
(2.73) |
||
|
|
|
|
|
|||||
|
|
dt |
|
1 A |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
dCD k |
C C2 |
; |
|
|
|||||
|
dt |
2 |
B C |
|
|
|
|||
|
|
|
|
|
|
|
|||
dCC =2k C |
2k C2 |
, |
|||||||
dt |
1 |
A |
|
2 |
C |
|
|||
|
|
|
|
|
|
|
|
|
|
где СА, СС, СD – концентрации веществ, моль/л.
Систему обыкновенных дифференциальных уравнений (ОДУ) первого порядка (2.73) можно решить с использованием алгоритмов численных методов решения ОДУ (Эйлера, Рунге-Кутты [11]).
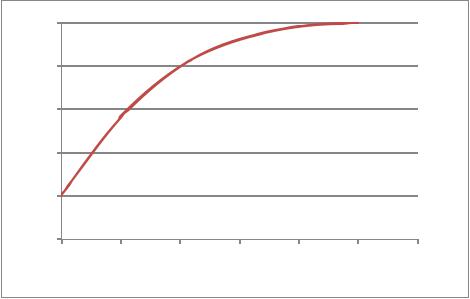
На рис. 2.9, 2.10 приведены результаты исследования влияния температуры на степень превращения исходного реагента и на концентрацию веществ с применением математической модели (2.73).
Полученные результаты позволяют сделать вывод об оптимальном времени проведения процесса с целью получения целевого продукта. Математическая модель (2.73) также позволяет исследовать влияние состава сырья на выход продуктов реакции.
Известно, что скорость химической реакции зависит от температуры, поэтому, чтобы исследовать влияние температуры на ход процесса, необходимо в кинетической модели (2.73) константу скорости химической реакции выразить по уравнению Аррениуса (2.70).
Рис. 2.9. Изменение концентрации реагирующих веществ
51
с течением времени
Рис. 2.10. Зависимость степени превращения исходного вещества от температуры
2.4.3. Моделирование кинетики гетерогенных химических реакций
Основы гетерогенной химической кинетики заложены в работах Лэнгмюра, Темкина и др. [20, 21, 23, 24]. В этих работах сформулировано понятие идеального адсорбированного слоя, базирующееся на аналогии с представлениями гомогенной кинетики. Эта модель использует следующие предположения:
равноценность всех участков поверхности катализатора и независимость энергии хемосорбции от степени заполнения поверхности различными адсорбентами;
неизменность катализатора и независимость его свойств от состава реакционной смеси и ее воздействия на катализатор;
равновесное распределение энергии.
Формальным аналогом кинетического закона действующих масс
для элементарных процессов на твердых поверхностях является закон действующих поверхностей (ЗДП) [20, 21].
Согласно его первоначальной формулировке скорость химической реакции пропорциональна произведению поверхностных концентраций реагирующих веществ в степенях, равных стехиометрическим соотношениям, в которых они вступают во взаимодействие (2.74):
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
. (2.74) |
|||
W kQZ11 |
QZ22 |
... QZ0 |
W k z1i z22 |
... z0 |
k zii z0 |
|||
|
|
|
|
|
|
i 1 |
|
|
52
где k – константа скорости; Zi – доля поверхности, занятой i-й адсорбированной частицей; Z0 – доля свободной поверхности; i – стехио-
метрические коэффициенты стадий; – изменение числа молей при протекании химической реакции.
Пусть протекает элементарная химическая реакция
|
A |
2 |
A |
... ' |
A' |
' |
A' |
.... |
(2.74а) |
1 |
1 |
2 |
1 |
1 |
2 |
2 |
|
|
При этом все вещества вступают во взаимодействие из адсорбированного состояния.
Обозначим: zi – доля поверхности, занятая i-м адсорбированным веществом. Тогда, в соответствии с законом действующих поверхностей, скорость необратимой реакции (2.74а) можно записать как
n
W k zii k z1i z22 z0 . (2.75)
i 1
Если не все вещества вступают во взаимодействие из адсорбированного состояния, а реагируют непосредственно из газовой фазы, то в более общем виде выражение закона действующих поверхностей можно представить следующим образом:
|
n |
|
|
m |
|
|
|
|
|
zi |
j |
|
|
||||
W k |
|
|
i |
|
C |
j |
, |
(2.76) |
|
|
|
|
|||||
|
i 1 |
|
|
j 1 |
|
|
|
|
где C j – парциальные давления (концентрации) j-веществ, реагирую-
щих из газовой фазы; n, m – количество веществ, адсорбированных на поверхности катализатора и реагирующих из газовой фазы.
Например, пусть протекает адсорбция водорода на активном центре катализатора Z с образованием адсорбированного поверхностного соединения ZH2:
H2 Z k ZH2 ,
тогда на основании ЗДП скорость данной элементарной химической реакции можно записать как
Wk Z CH2 .
Вкачестве основного фактора, определяющего кинетические зависимости, вначале рассматривался фактор вытеснения, «борьбы» компонентов реакционной смеси за места на поверхности катализатора. При этом принималось дополнительное предположение о высокой скорости адсорбционных и десорбционных стадий по сравнению с собственно химическими превращениями.
53
Последующие исследования показали существенную ограниченность этих предположений. Тем не менее Хиншельвудом, Швабом, Хоугеном, Ватсоном и другими получены уравнения, удовлетворительно описывающие кинетический эксперимент в определенном интервале изменения параметров [24].
Общая формула кинетического уравнения, соответствующего этим предположениям, имеет следующий вид:
|
n |
vi |
|
n |
|
, |
W k Ci |
1 |
kpi Ci |
||||
|
i 1 |
|
|
i 1 |
|
|
где k – константа скорости; Сi – концентрация i-го реагента газовой среды; kpi – константа равновесия стадии адсорбции i-го компонента; i –
стехиометрические коэффициенты.
Пример
Рассмотрим сложную гетерогенную химическую реакцию гидрокрекинга толуола.
Детальный механизм гетерогенной химической реакции:
Здесь Z – активные центры на поверхности катализатора; ZH2 и т. д. – адсорбированные промежуточные соединения.
Запишем скорости элементарных стадий механизма по закону действующих поверхностей:
r1 k1 CH2 Z; r 1 k 1 ZН2 ;
r2 k2 CC7H8 ZH2 ;
r3 k3 ZC7H8 H2 ;
r 3 k 3 CC6H6 CCH4 Z .
Математическая модель данного химического процесса будет представлять собой систему дифференциальных уравнений, выражающих изменение концентраций наблюдаемых веществ и промежуточных соединений во времени:
54
dC |
H2 |
|
r1 r 1; |
|
|
|
||||||||||
|
|
|
|
|
|
|||||||||||
dt |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
dCC |
H |
8 |
|
|
r ; |
|
|
|
|
|
||||||
|
|
7 |
|
|
|
|
|
|
|
|
|
|||||
dt |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dCCH |
4 |
|
|
|
r |
|
r |
|
; |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
dt |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
3 |
3 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dCC |
H |
6 |
|
|
r3 |
r 3; |
|
|
|
|||||||
|
|
6 |
|
|
|
|
|
|
(2.77) |
|||||||
dt |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
d Z |
r |
r |
r r ; |
|||||||||||||
|
dt |
|
|
|
|
1 |
|
|
1 |
|
3 |
3 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d ZН |
|
|
|
r |
r |
r ; |
|
|
||||||||
|
|
2 |
|
|
|
|
||||||||||
|
|
|
|
|
|
|||||||||||
dt |
|
|
|
1 |
|
1 |
|
2 |
|
|
|
|||||
|
d ZC7H8 H2 |
|
|
|
|
|
|
|
|
|||||||
|
|
r |
r |
r |
. |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
dt |
|
|
|
|
|
|
2 |
|
3 |
3 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
При решении системы дифференциальных уравнений (2.77) можно использовать численные методы Эйлера и Рунге-Кутты.
Методы построения кинетических моделей гетерогенных химических реакций
Метод, основанный на элементах теории Ленгмюра
Сформулируем алгоритм построения кинетической модели гетерогенной химической реакции методом Лэнгмюра.
1.Записывается механизм гетерогенной химической реакции в виде совокупности элементарных стадий.
2.Записываются выражения скоростей реакций элементарных стадий на основании закона действующих поверхностей.
3.Определяется лимитирующая стадия. Все остальные стадии являются быстрыми и равновесными.
4.Для равновесных стадий приравниваются скорости в прямом и обратном направлениях и концентрации промежуточных соединений выражаются через концентрацию промежуточного соединения, участвующего в лимитирующей стадии и концентрации наблюдаемых веществ.
5.В результате решения системы алгебраических уравнений определяются выражения для концентрации промежуточного соединения, входящего в уравнение скорости лимитирующей стадии, через концентрации наблюдаемых веществ и константы скоростей эле-
55
ментарных стадий. При этом используется уравнение нормировки, в котором количество активных центров на поверхности катализатора принято равным единице и равно сумме долей поверхности катализатора, занятых промежуточными соединениями и свободными центрами.
6.Записывается выражение скорости гетерогенной химической реакции по лимитирующей стадии.
Пример. Рассмотрим вывод выражения скорости для следующей гетерогенной химической реакции:
По закону действующих поверхностей запишем скорости элементарных стадий:
r1 k1 z CA ; r 1 k 1 zA ; r2 k2 zA ; r3 k3 zB ; r 3 k 3 z CB .
Примем вторую стадию за лимитирующую и запишем выражение скорости стадии по ЗДП:
W r2 k2 zA . |
(2.78) |
В этом выражении необходимо выразить концентрацию промежуточного соединения θzA через концентрации наблюдаемых компонентов.
Все остальные стадии будем считать быстрыми и равновесными. В этом случае скорость прямой реакции равна скорости обратной:
k1 z CA k 1 zA ; |
(2.79) |
k3 zB k 3 CB z . |
Выразим z :
z k 1 zA . k1 CA
56
Запишем уравнение нормировки zA zB + z 1и решим систему алгебраических уравнений (2.79) относительно θzA:
|
|
|
|
|
k 1 |
|
|
|
|
k 1k 3CB |
|
|
||||||||||||
zA 1 |
|
|
|
1; |
||||||||||||||||||||
|
|
k1k3CA |
||||||||||||||||||||||
|
|
|
|
|
k1 CA |
|
|
|||||||||||||||||
zB |
k 3CB z |
|
k 1k 3CB zA |
; |
|
|
||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
k3 |
|
|
|
|
|
|
|
k1k3CA |
||||||||||
zA |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
; |
|
|
|||||||
1 |
|
k 1 |
|
|
k 1k 3CB |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
k C |
|
|
|
|
k k C |
A |
|||||||||||
|
|
|
|
|
|
|
|
1 A |
1 3 |
|
||||||||||||||
zA |
|
|
|
|
|
|
|
k1k3CA |
|
|
|
|
|
|
|
|
; |
|||||||
k1k3CA |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
k 1k3 k 1k 3CB |
||||||||||||||||||||||
W |
|
|
|
|
|
|
|
k1k2k3CA |
|
|
|
|
|
|
|
. |
||||||||
k k C |
|
k |
|
k |
k |
k |
C |
|||||||||||||||||
|
|
|
1 3 A |
|
|
|
1 3 |
|
1 |
|
3 B |
|||||||||||||
Метод стационарных концентраций
Стационарным считается такой режим, при котором параметры в каждой точке системы в заданный промежуток времени сохраняются постоянными.
Так как скорость химического процесса существенно зависит от концентраций промежуточных веществ, то при стационарном режиме ее протекания концентрации промежуточных соединений должны оставаться постоянными. Таким образом, стационарность протекания химической реакции означает стационарность концентраций промежуточных соединений, которые должны успевать многократно возникнуть и разложиться в ходе химической реакции, уступая место другим промежуточным соединениям. Тогда условие стационарности можно выразить следующим образом [23]:
d i 0. dt
Выполнение условия стационарности означает, что алгебраическая сумма скоростей образования и расходования каждого из промежуточных соединений равна нулю. Для реализации стационарного режима необходимо сохранение постоянства внешних параметров режима, а для гетерогенных каталитических реакций – и постоянство каталитической активности катализатора.
Сформулируем алгоритм построения кинетической модели гетерогенной химической реакции методом стационарных концентраций:
57

1.Записывается механизм гетерогенной химической реакции в виде совокупности элементарных стадий.
2.Записываются выражения скоростей реакций элементарных стадий на основании закона действующих поверхностей.
3.Записывается условие стационарности по промежуточным соединениям.
4.Решается полученная система алгебраических уравнений и определяются выражения для концентраций промежуточных соединений.
5.Записывается выражение скорости гетерогенной химической реакции по любой стадии.
Пример. Составить выражение скорости для гетерогенной химиче-
ской реакции.
Механизм химической реакции:
1. A+z |
|
k1 |
|
zA |
||||
|
|
|
|
|
|
|||
|
|
k-1 |
|
|||||
|
|
|
|
|
|
|||
2. zA |
|
k2 |
|
z+B |
||||
|
|
|||||||
|
|
|
|
|
||||
|
|
k-2 |
|
|
||||
А=В
Скорости элементарных реакций:
W1 r1 r-1 ;
W2 r2 r 2.
Запишем выражения для скоростей элементарных стадий по закону действующих поверхностей:
r1 k1 CA z , r2 k2 zA ; r 1 k 1 zA , r 2 k 2 CB z .
Условие стационарности:
dCdtz 0; dCdtzA 0;
dCz |
r r |
r r |
0; |
|
|
dt |
1 1 |
2 2 |
(2.80) |
|
||||
|
|
|
||
dCzA |
r1 r 1 r2 r 2 0. |
|||
|
dt |
|||
|
|
|
|
|
Используя уравнение нормировки
z zA |
1, |
58

преобразуем систему уравнений (2.80) к следующему виду:
k1CA z k 1 zA k2 zA k 2CB z 0;
zA k 1 k2 z k1CA k 2CB ;
|
z |
|
|
k 1 k2 |
|
zA; |
|
|
||||||||||||
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
k1CA k 2CB |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
k 1 k2 |
|
|
|
|
|
|
|
|
|
|||||
zA 1 |
|
|
|
|
|
1; |
|
|
||||||||||||
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
k1CA k 2CB |
|
|
|
|
|
||||||||||
|
zA |
|
|
|
|
1 |
|
|
|
|
|
|
|
; |
|
|
||||
|
1 |
k 1 |
k2 |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
k C |
A |
k |
2 |
C |
B |
|
|
||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
||||||||
zA |
|
|
|
|
k1CA k 2CB |
|
|
|
|
; |
||||||||||
|
k1CA k 2CB |
k 1 k2 |
|
|||||||||||||||||
|
|
|
|
|
||||||||||||||||
r2 |
|
|
|
k2 k1CA k |
2 k 2CB |
. |
||||||||||||||
k1CA k 2CB |
k 1 k2 |
|||||||||||||||||||
|
|
|
|
|||||||||||||||||
Так как реакция обратимая, находим выражение скорости r–2:
z |
k 1 k2 |
|
(k1CA k 2CB ) |
. |
(k1CA k 2CB ) |
|
|||
|
|
k1CA k 2CB k 1 k2 |
||
В результате преобразований получим
z k1CA kk 21CB k2 k 1 k2 .
Подставим полученное выражение в r–2:
|
|
|
r |
|
k 2 k 1CB k 2 k2CB |
. |
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
2 |
|
|
|
k1CA k 2CB k 1 k2 |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
В результате получим выражение скорости реакции |
|
|
|
|||||||||||||||||||||||||||||
W =r -r |
= |
k2 k 1CA k2 k 2CB |
|
|
k 2 k 1CB k 2 k2CB |
; |
||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||
2 -2 |
|
k C |
k |
2 |
C |
B |
k |
1 |
k |
2 |
|
k C |
k |
2 |
C |
B |
k |
1 |
k |
2 |
|
|||||||||||
|
|
1 A |
|
|
|
|
|
|
|
|
|
|
1 A |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
W = |
|
k1k2CA k 1 k 2CB |
. |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
k C |
A |
k |
2 |
C |
B |
k |
1 |
k |
2 |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Если в механизме есть хоть одна необратимая стадия, то весь процесс становится необратимым.
59
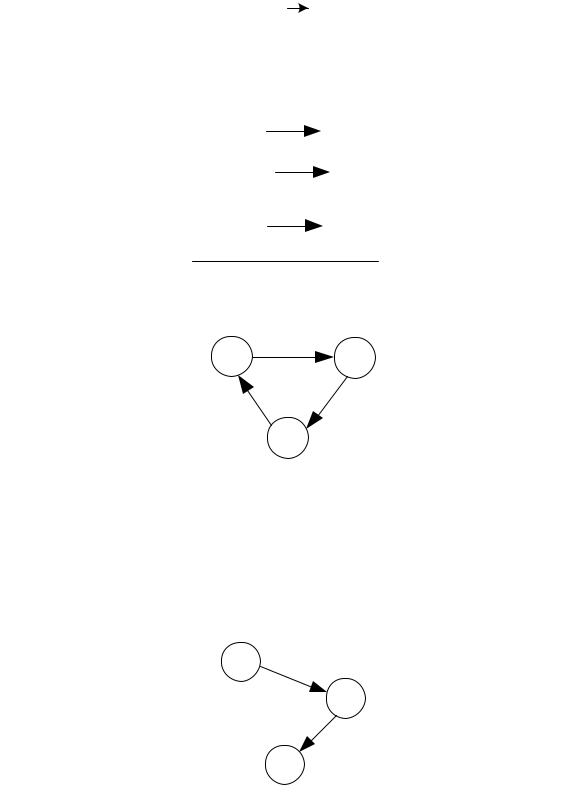
Метод построения кинетических моделей с использованием элементов теории графов
Рассмотрим вывод выражения скорости на примере следующей реакции:
.
Механизм реакции представим в виде последовательности элементарных стадий:
Граф для данного механизма реакции представим в виде
Всякое графическое изображение конечного множества элементов и взаимосвязей между ними называется графом. Граф состоит из вер-
шин (узлов) и ребер (или дуг)[20].
Дуга – это линия, соединяющая вершины графа. Цикл – замкнутая совокупность дуг.
Дерево граф (каркас) – незамкнутая совокупность дуг, проходящих через все вершины графа и входящих в данную вершину.
Например, дерево граф для вершины zC:
60
