
Вопросы к зачету с оценкой
по дисциплине: «Моделирование химико-технологических процессов»
(весенний семестр 2021/2022 уч. год - бакалавры)
Моделирование стационарного режима изотермического процесса химического превращения в проточном реакторе идеального перемешивания с простейшей стехиометрией последовательной реакции A-P-S. Определение оптимального времени пребывания потока в реакторе.



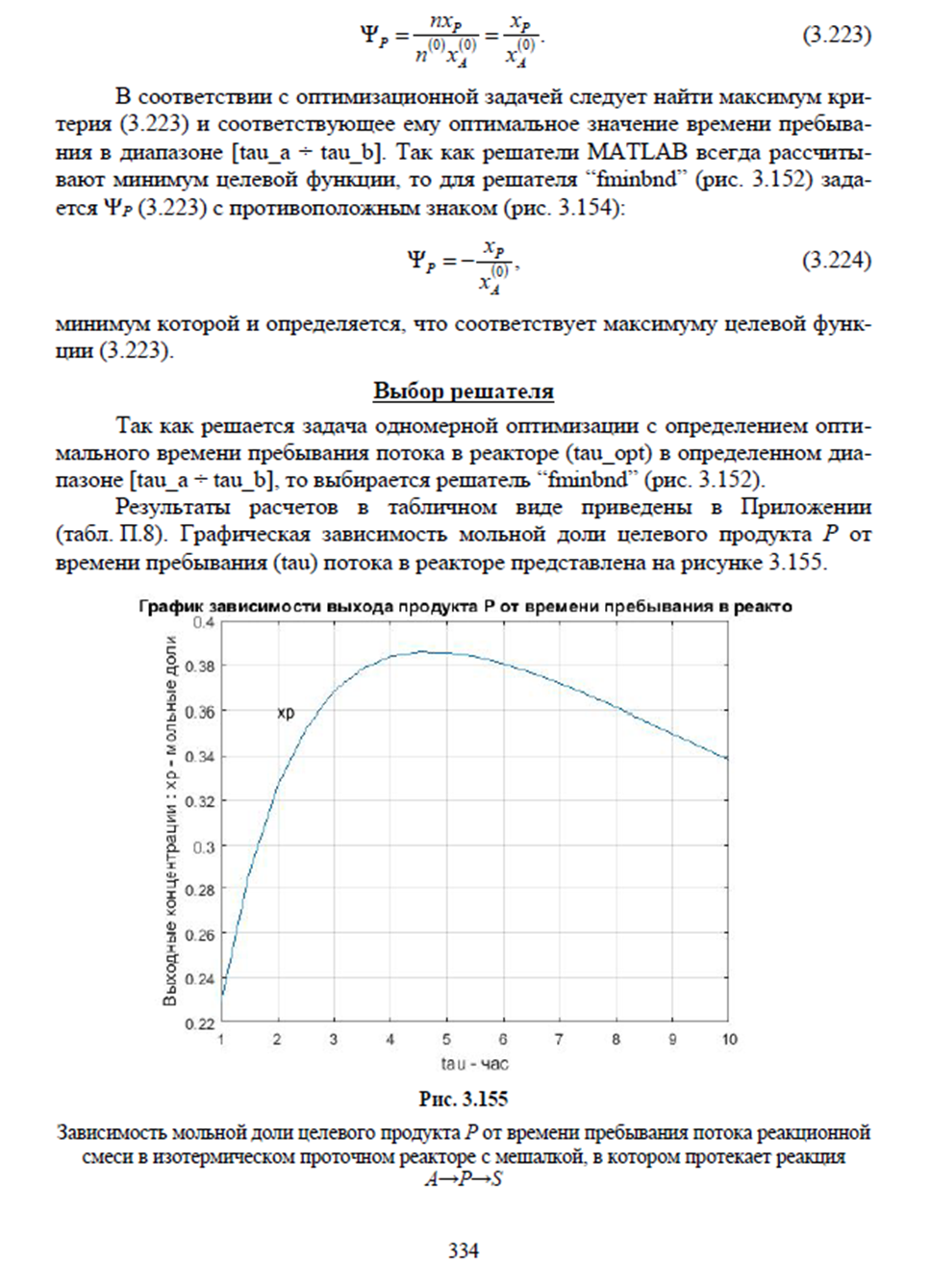
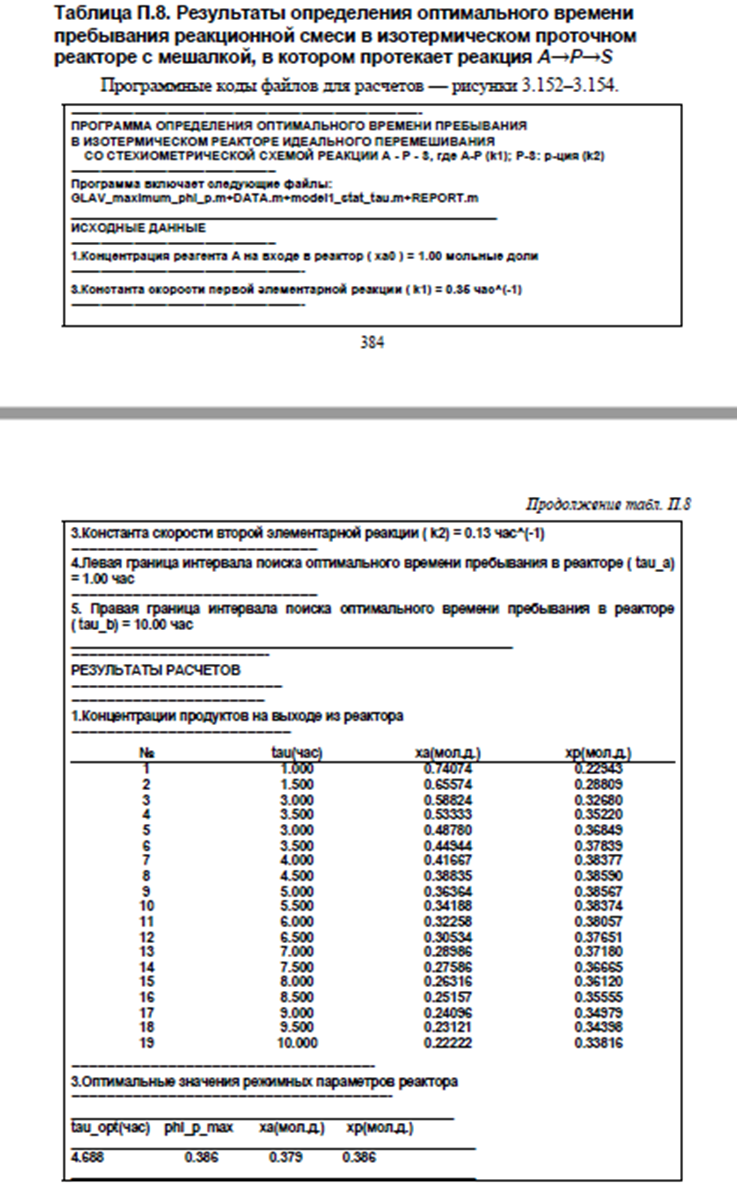
Моделирование стационарного режима изотермического процесса химического превращения в проточном реакторе идеального перемешивания с простейшей стехиометрией обратимой реакции A=P. Определение оптимальной температуры в в реакторе.




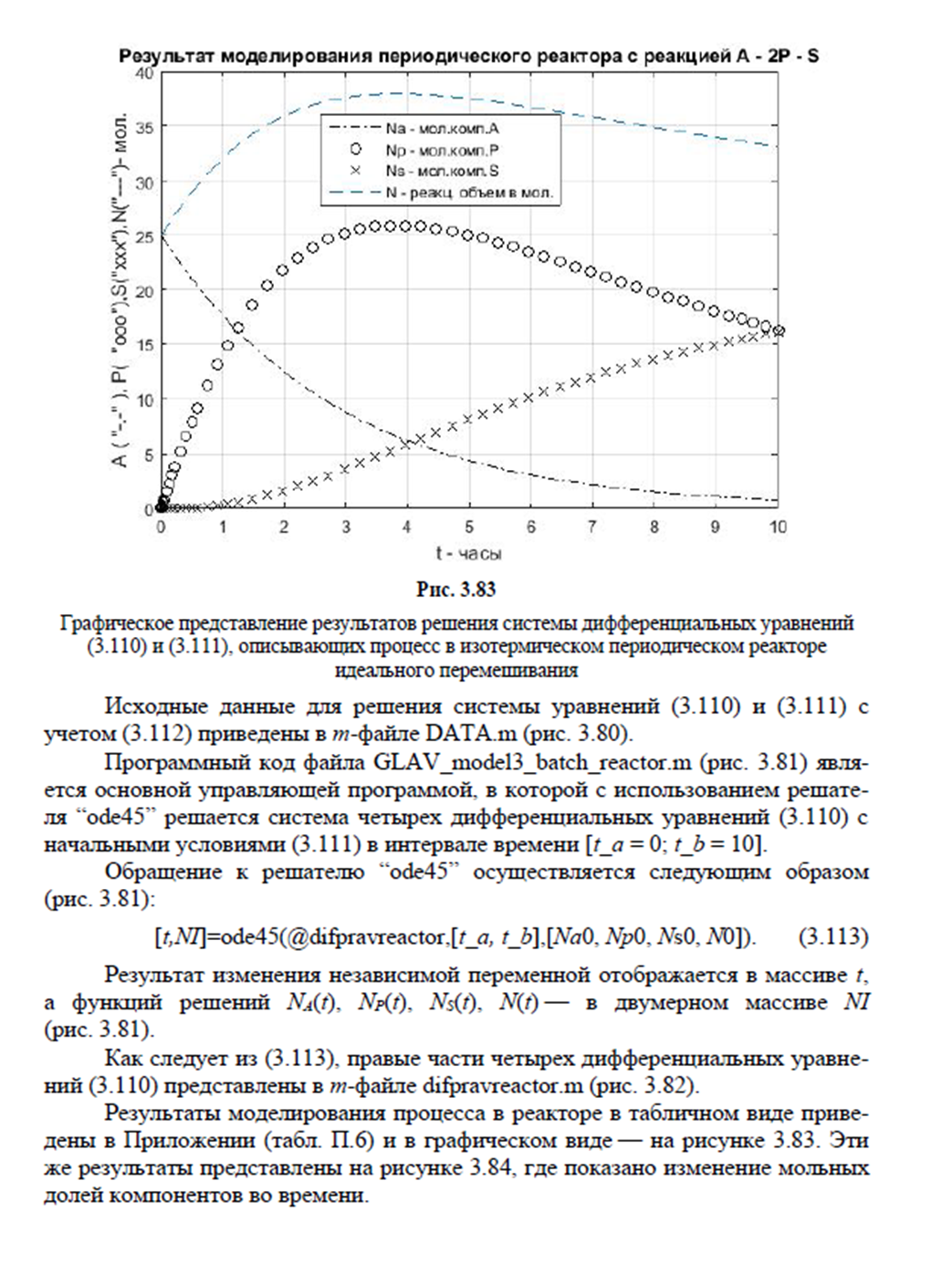
Моделирование изотермического процесса химического превращения в периодическом реакторе с мешалкой с последовательной реакцией A-P-S и определение оптимального времени реакции.



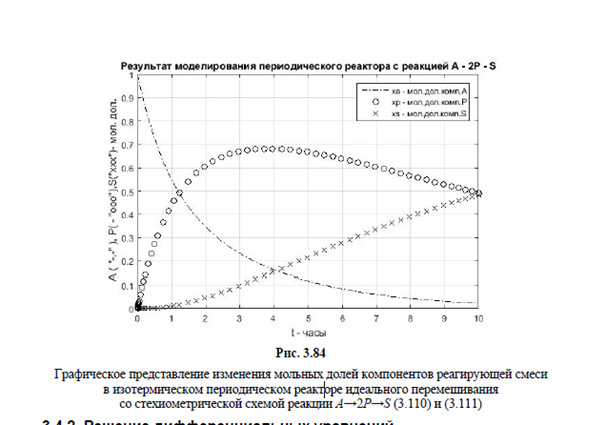


Моделирование стационарного процесса теплопередачи с движущимися потоками типа “смешение-смешение”. Математическое описание процесса и принимаемые допущения. Математическая формулировка задачи и алгоритмы её решения.


Моделирование стационарного процесса теплопередачи с движущимися потоками типа “смешение-вытеснение”. Математическое описание процесса и принимаемые допущения. Математическая формулировка задачи и алгоритмы её решения.
ГАРТМАН 2008 С.289-292
https://elib.belstu.by/bitstream/123456789/32074/1/Matys_modelirovanie_2019.pdf (Дополнительная информация по вопросу, более кратко)



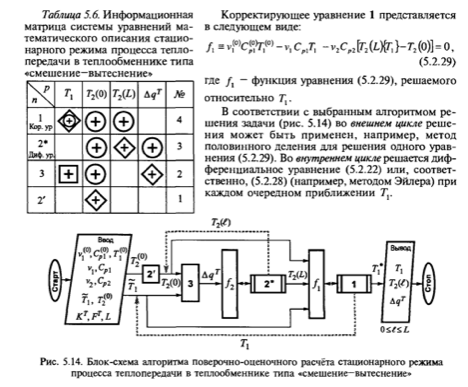
Моделирование стационарного процесса теплопередачи с движущимися потоками типа “вытеснение-вытеснение (прямоток)”. Математическое описание процесса и принимаемые допущения. Математическая формулировка задачи Коши с начальными условиями и алгоритмы её решения.
ГАРТМАН 2008 С.292-294
https://elib.belstu.by/bitstream/123456789/32074/1/Matys_modelirovanie_2019.pdf (Дополнительная информация по вопросу, курсу)


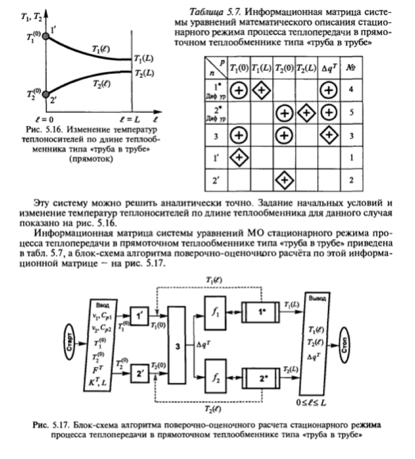
Моделирование стационарного процесса теплопередачи с движущимися потоками типа “вытеснение-вытеснение (противоток)”. Математическое описание процесса и принимаемые допущения. Математическая формулировка краевой задачи и алгоритмы её решения.
Моделью вытеснение – вытеснение описываются, например, аппараты типа труба в трубе.



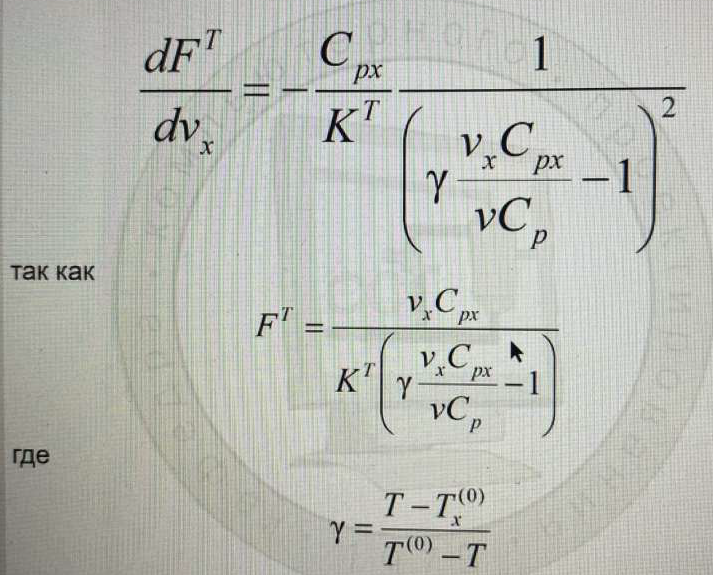
Оптимизация стационарного процесса теплопередачи с движущимися потоками типа “смешение-смешение” при требуемой тепловой нагрузке с целью определения оптимальной площади поверхности теплопередачи и оптимального расхода одного из теплоносителей. Выбор экономического критерия оптимальности для решения задачи. Обоснование выбора ресурса оптимизации (оптимизирующей переменной).
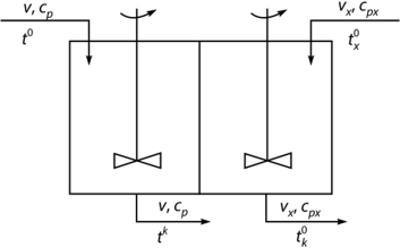
Теплообменник типа «смешение — смешение». Математическое описание этого теплообменника (рис. 2.5) задают системой двух уравнений, относящихся к обоим теплоносителям (типа (2.15)). Интенсивность источника тепла Q при этом равна скорости теплопередачи через стенку по уравнению Ньютона (1.67). При стационарном режиме работы теплообменника в уравнениях (2.15) производные по времени равны нулю.
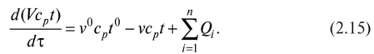
В результате будет справедлива следующая система уравнений соответственно для горячего и холодного теплоносителя
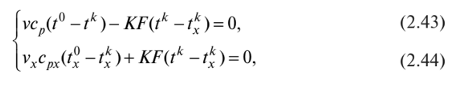
которая может быть решена относительно двух любых параметров, входящих в эти уравнения. В частности, для выходных температур горячего ft и холодного ft теплоносителей можно получить соответственно выражения:
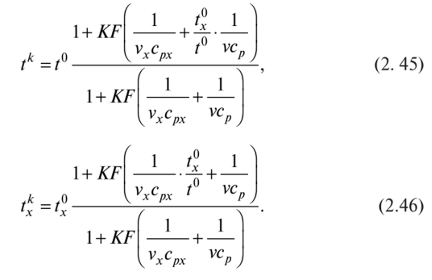
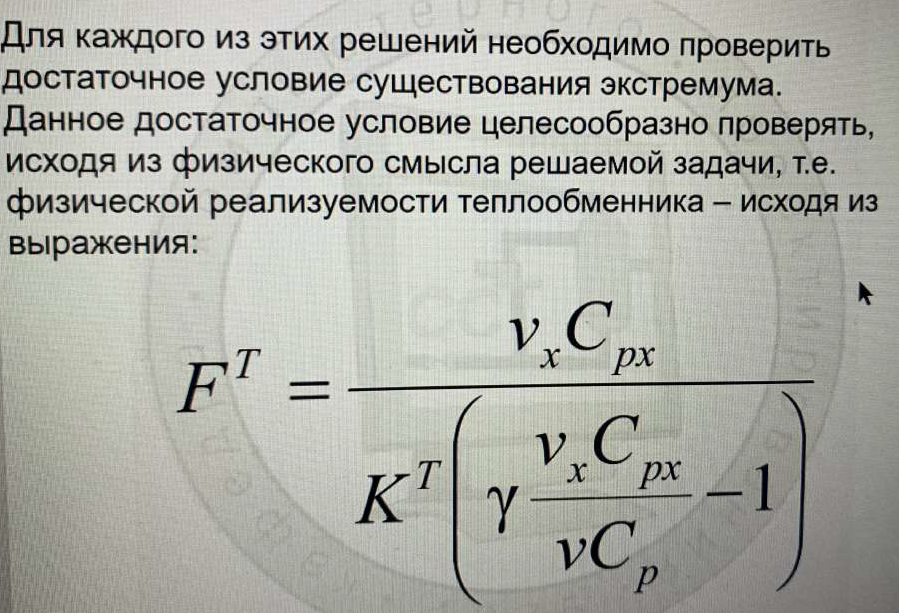
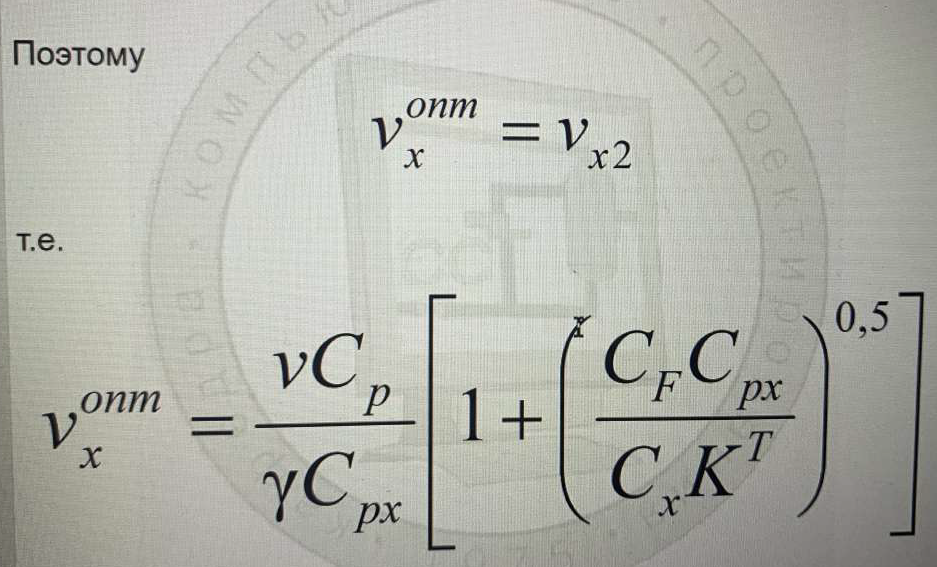
(Критерий приведенных затрат – расход хладагента νx (оперативные) и площадь поверхности теплопередачи FT (капитальные). Сумма этих величин должна быть минимальной. Стоимость хладагента должна быть минимальной и площадь поверхности или стоимость железа должна быть наименьшей. Физические величины поэтому умножаем на стоимостные коэффициенты.
Необходимо найти оптимальный расход теплоносителя и оптимальную площадь поверхности. Благодаря модели, которую мы используем, FT и νx связаны между собой. Зная площадь поверхности, можно выбрать необходимый теплообменник.)



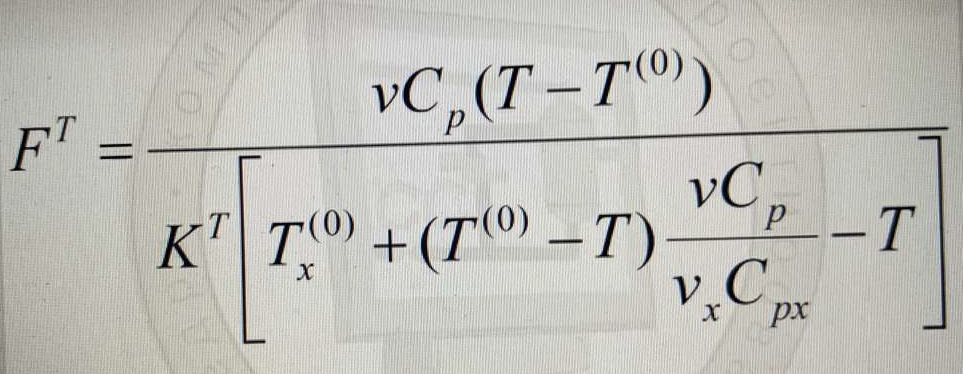



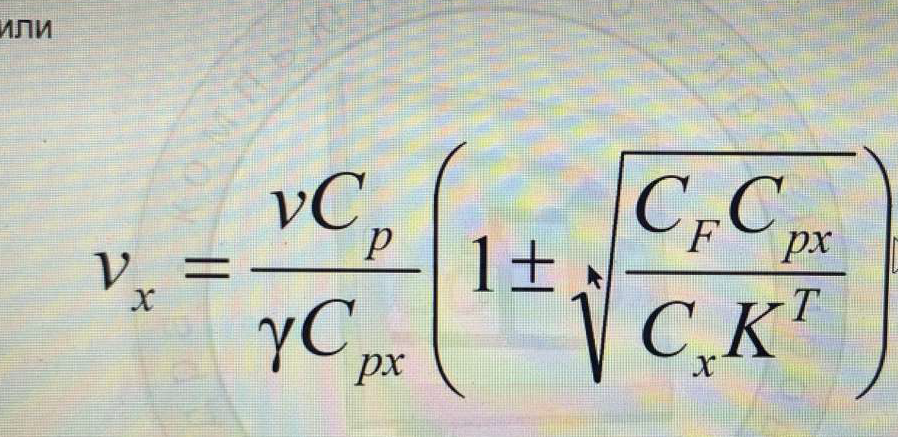




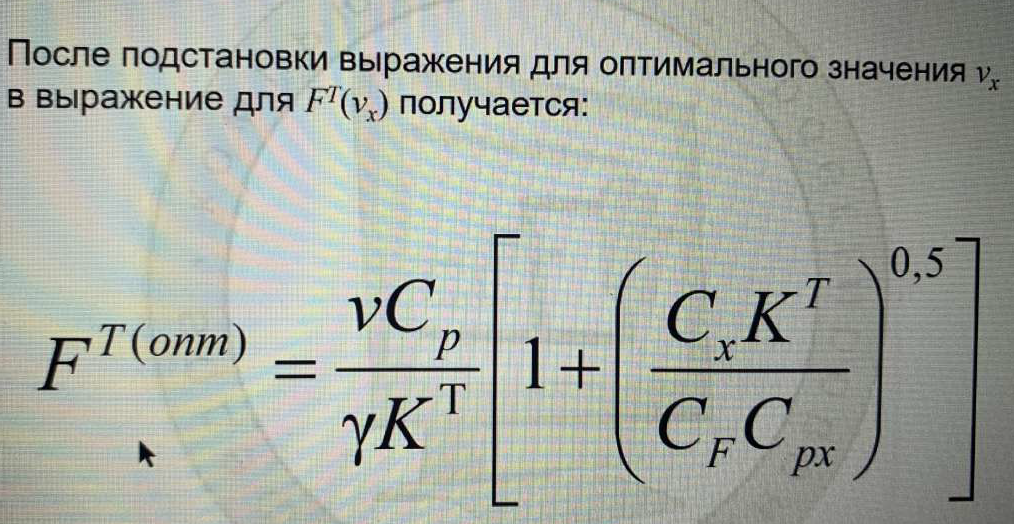
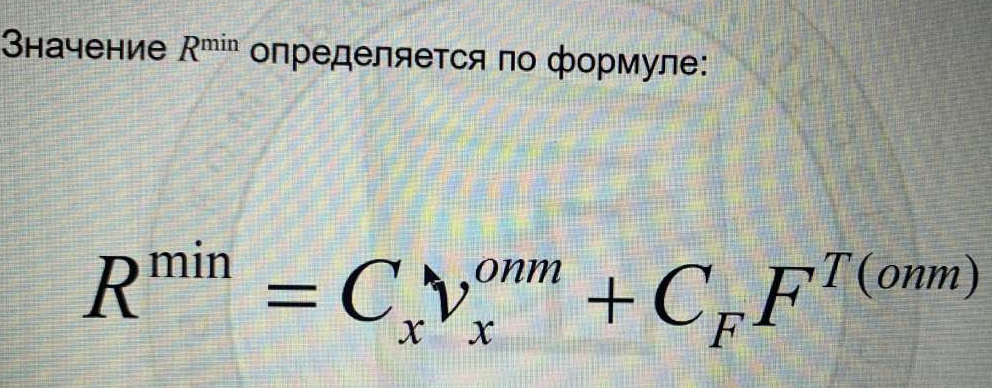
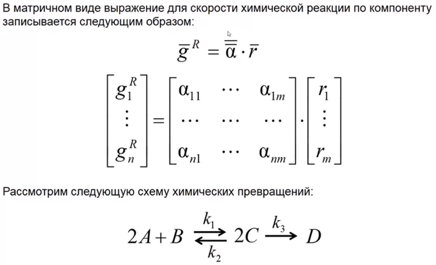
Моделирование микрокинетики произвольной химической реакции. Формирование матрицы стехиометрических коэффициентов сложной химической реакции. Определение числа ключевых компонентов химической реакции с применением матрицы стехиометрических коэффициентов. Закономерности для вычисления скоростей отдельных стадий химической реакции и скоростей реакции по отдельным компонентам. Задание температурной зависимости констант скоростей реакции. Определение скорости выделения (поглощения) тепла в химических реакциях. Учет тепловых эффектов отдельных стадий экзотермических и эндотермических реакций.

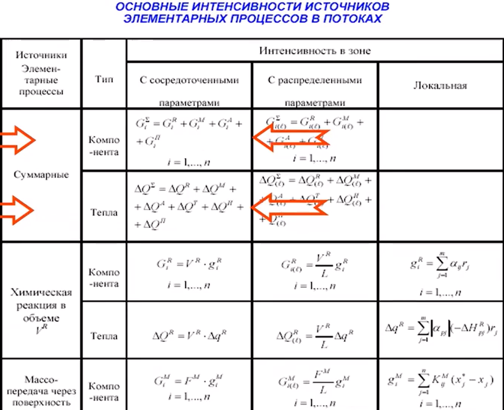
![]() – локальный
источник компонента i-го за счёт химической
реакции.
– локальный
источник компонента i-го за счёт химической
реакции.
m – количество стадий
n – количество веществ в реакторе
ɑ - стехиометрические коэффициенты
r – скорость реакции (скорость стадии).
R – источник тепла за счёт химической реакции.
j – количество стадий
Для таблицы ниже:
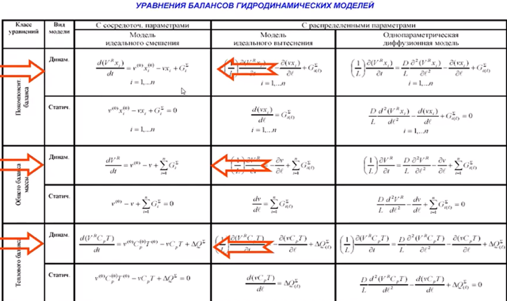
Сосредоточенные параметры – относятся к модели идеального смешения.
Распределённые параметры – относятся к модели идеального вытеснения.
Верхние индексы:
R – химическая реакция
М – массопередача
Λ – изменение агрегатного состояния
n – подпитка тепла
Т – теплопередача
И – теплоизоляция


k – константа скорости
Матричная форма расчёта:
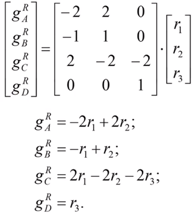
“ – “ – если вещество убывает.


Ключевые компоненты нужны, чтобы на микроуровне сократить количество уравнений.





Математическое описание стационарного гомогенного процесса в проточном реакторе с мешалкой и рубашкой с произвольной стехиометрией реакции. Выбор алгоритма решения прямой задачи моделирования с применением информационной матрицы системы уравнений математического описания. Блок-схема алгоритма решения задачи моделирования.
Вначале следует изучить теорию процесса в конкретном реакторе.
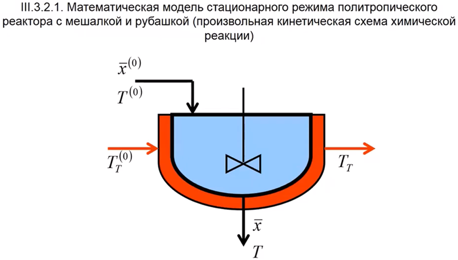
Политропический реактор обеспечивает изменение тепла за счёт химической реакции и теплообмена. Теплообмен может происходить за счёт теплоносителя или теплообменника (в данном случае рубашка), либо за счёт обмена с окружающей средой.
В данном случае и в реакторе, и в рубашке осуществляется модель идеального смешения.
Сверху - входные параметры веществ и температуры, по бокам- входная и выходная температура теплоносителя, снизу- выходные параметр реактора

Математическое описание:
Первые n-уравнения – покомпонентный баланс для каждого вещества.
Во 2-м уравнении определяют источник компонента за счёт химической реакции. В 3-м уравнении определяется скорость реакции – этих уравнений будет столько же, сколько реакций. В 4-м уравнении определяется константа скорости для каждой реакции – этих уравнений столько же, сколько и реакций (или стадий).
5-е уравнение – уравнение общего материального баланса (во всём реакторе). V – реакционный объём.

Далее идут тепловые балансы:
6 – тепловой баланс в реакторе – включает изменение тепла за счёт входного потока, химической реакции и теплопередачи. F – поверхность теплопередачи, ∆ – изменение тепла за счёт теплопередачи.
7 – изменение тепла за счёт химической реакции.
8 – изменение тепла за счёт теплопередачи. – коэффициент теплопередачи. – поток теплоносителя (вспомогательный поток) или температура окружающей среды, Т – температура в реакторе.
9 – общая теплоёмкость потока, складывается из теплоёмкостей индивидуальных веществ. – концентрация индивидуального вещества.
10 – количество уравнений = количеству веществ. Теплоёмкость индивидуального вещества по формуле зависимости от температуры.
11 – относится к теплоносителю. Тепловой баланс в теплоносителе. 6 и 11 уравнения – разница в знаках ∆.
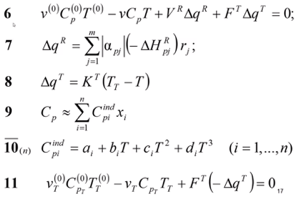
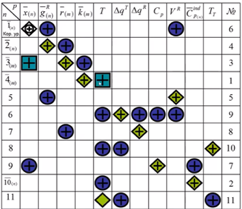
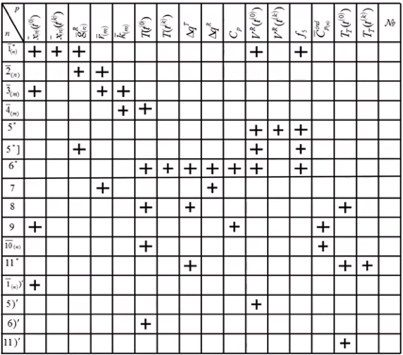
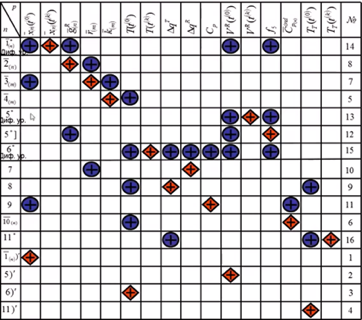
Построение информационной матрицы.
Информационная матрица строится, чтобы определить оптимальный порядок решения системы уравнений.
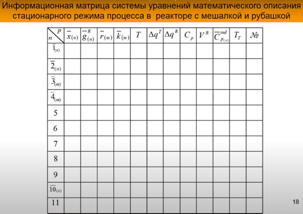
Вначале проставляются крестики, в какие уравнения входят неизвестные значения. Далее задаётся начальное приближение по температуре – обводим в квадрат. Температура хороша в качестве начального приближения тем, что она имеет диапазон изменения (не может быть ниже, чем температура стеклования и выше, чем температура разложения вещества), входит в большое число уравнений, её задание помогает запустить решение системы уравнений.
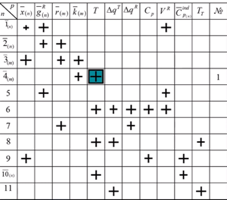
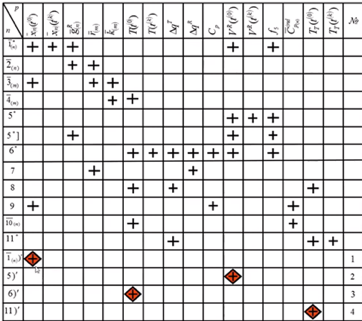
Ромб – посчитанное, кружок – уже найденное.
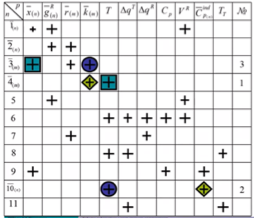
Задается начальное приближение по концентрации ключевого компонента. Не ключевые компоненты будут обводиться ромбиками.
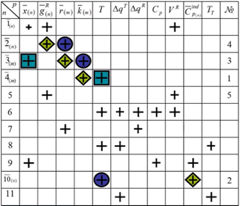
Рассчитываем g.
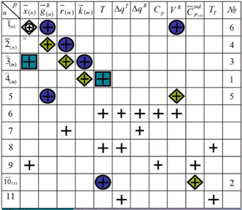
6 – корректирующее уравнение по веществу х.
В 11 уравнении 2 известные величины, поэтому оно тоже может быть корректирующим (по температуре).
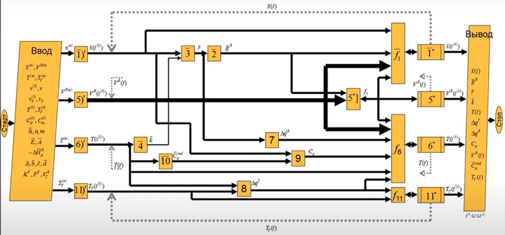
Строим блок-схему по данным из таблицы.
Пунктиром сверху обозначена первая итерация.
Т с волнистой линией задали температуру в реакторе, а ТТ- температура теплоносителя.
Нижняя пунктирная линия- вторая итерация, для задания температуры в реакторе, если было сделано что-то неправильно. (11- проверочное уравнение)

Математическое описание нестационарного гомогенного процесса в проточном реакторе с мешалкой и рубашкой с произвольной стехиометрией реакции. Выбор алгоритма решения прямой задачи моделирования с применением информационной матрицы системы уравнений математического описания. Блок-схема алгоритма решения задачи моделирования.
Динамический режим отличается тем, что параметры (концентрации) изменяются во времени.

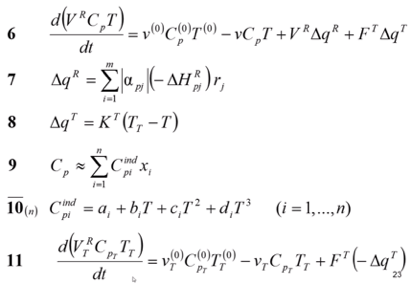
5 (общий материальный баланс) – дифференциальное уравнение по реакционному объёму и 6 (тепловой баланс) – по изменению температур во времени.
∆q^R – изменение тепла за счёт химической реакции; не меняется по сравнению со стационарным режимом, так как это микроуровень.
∆q^T – изменение тепла за счет теплопередачи.
9 – общая теплоёмкость, 10 – теплоёмкость каждого индивидуального вещества в зависимости от температуры.
11 – тепловой баланс для теплообменника.





Информационная матрица системы уравнений математического описания нестационарного режима процесса в реакторе с мешалкой и рубашкой:

Если нет теплообменника, то теплообмен с окружающей средой, и температуру окружающей среды в матрицу вставлять не нужно, так как она известна.
Сначала проставляем все неизвестные в каждом уравнении:
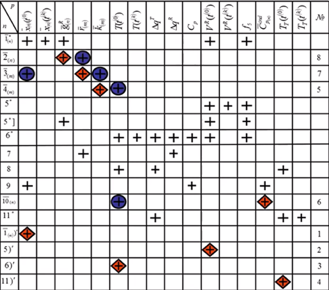
Красные ромбики – рассчитали значения параметров в начальный момент времени.
Синие кружки – посчитанные значения.
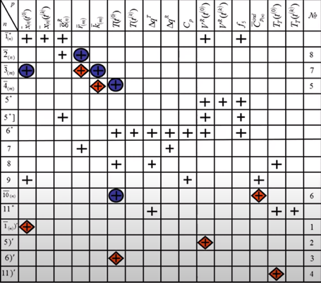
Когда стали известны скорости реакций, рассчитываем (источник компонента за счёт химической реакции):
Далее на основании информационной матрицы строим блок-схему – графическое изображение алгоритма, позволяющее более наглядно представить расчёты.
Итерации по всем 4-м заданным величинам.
Математическое описание стационарного гомогенного процесса в проточном трубчатом реакторе с рубашкой (теплоноситель движется в режиме прямотока) с конкретной стехиометрией реакции. Выбор алгоритма решения прямой задачи моделирования с применением информационной матрицы системы уравнений математического описания. Блок-схема алгоритма решения задачи моделирования.
По тепловым балансам 3 типа реакторов:
политропический – присутствуют все наполнения математического описания (полная математическая модель).
адиабатический – предполагает, что нет обмена с окружающей средой, работает по принципу термоса. Все изменения по теплу происходят внутри самого реактора. Изменение тепла происходит только за счёт тепла химической реакции. Некоторые уравнения будут отсутствовать.
изотермический – предполагается, что Т=const. Будет модель материального баланса, а тепловых балансов не будет. Самый простой по типу реактор (относится и к режиму смешения, и к режиму вытеснения).
По движению потоков 2 типа реакторов:
смешения
вытеснения – изменение параметров по длине реактора (трубы).
Математическая модель стационарного режима политропического процесса в трубчатом реакторе с прямоточным режимом движения теплоносителей в рубашке (конкретная кинетическая схема химической реакции):
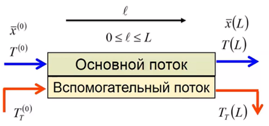
Для построения модели политропического трубчатого реактора примем следующие допущения:
рассматривается 2-х-стадийная 3-х-компонентная химическая реакция, протекающая по схеме:
![]()
движение основного потока (реакционной смеси) в реакторе и вспомогательного потока (теплоносителя в рубашке) представляется гидродинамическими моделями идеального вытеснения
параметры потока теплоносителя в рубашке (обозначаются нижним индексом «Т») неизменны, кроме температуры потока теплоносителя в рубашке
реакции в реакторе считаются гомогенными, без фазовых переходов
считается, что все процессы происходят в жидкой фазе, все реакции протекают одновременно
тепловые эффекты стадий химической реакции не зависят от температуры
при теплообмене между основным и вспомогательным потоками учитывается только теплопередача
коэффициент и площадь поверхности теплопередачи между основным и вспомогательным потоками постоянны и не изменяются
Режим идеального вытеснения предполагает «вытеснённые параметры»:


