Описание микрокинетики процесса в реакторе

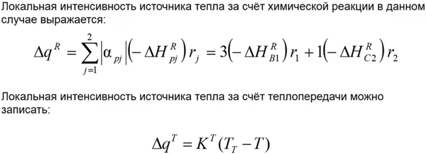
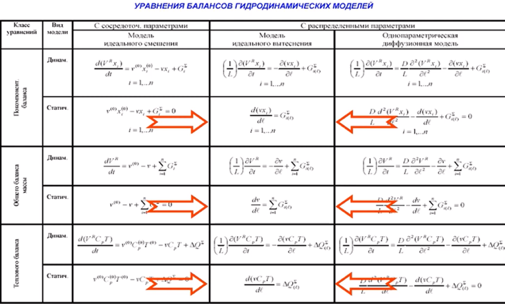
Построение математической модели стационарного режима процесса с прямоточным движением теплоносителя (решение задачи Коши):

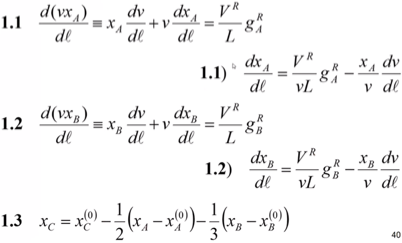
Первые 2 уравнения – определение ключевых компонентов. Хс выражается через 2 ключевых компонента. - начальное условие, – текущее значение С через концентрации А и В.

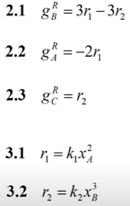
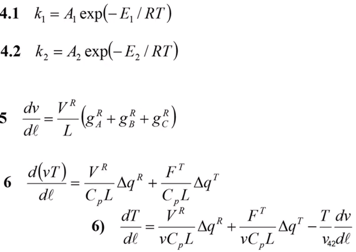
5 – определение скорости движения по длине реактора.

Если будет реактор изотермический, то 6 уравнения нет (т.к. Т=const).

6 – уравнение теплового баланса в реакторе - изменение температуры по длине.

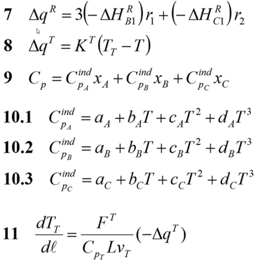
7 – определение изменения локального тепла за счёт химической реакции.

8 – локальное изменение тепла за счёт теплопередачи. – константа теплопередачи.

9 – общее значение теплоёмкости.

10 – индивидуальные значения теплоёмкостей.

11 – тепловой баланс теплоносителя. -∆q^T – минус, так как режим вытеснения и прямоток – два потока идут параллельно. В уравнении 6 и 11 должны быть разные знаки при ∆q^T (где-то поток охлаждается, а где-то нагревается).

Для определения частного решения системы обыкновенных дифференциальных уравнений необходимо решить задачу Коши, при этом задаются следующие начальные условия:

Если нет рубашки, но реактор политропический, то убирается уравнение 11, а в 8 на месте Тт ставится температура окружающей среды.

Если реактор адиабатический, то в 6-м уравнении не будет последнего члена (не будет изменение тепла за счёт теплообмена). Пропадут также 8 и 11 уравнения.

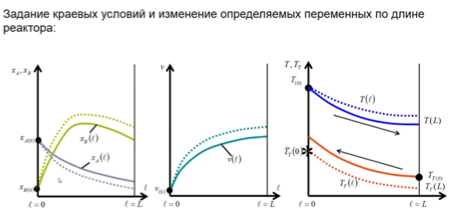
Задание начальных условий и изменение концентраций компонентов, расхода потока и температур реакционного и вспомогательного (теплового) потоков по длине реактора:

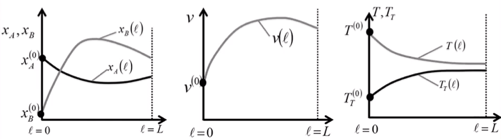
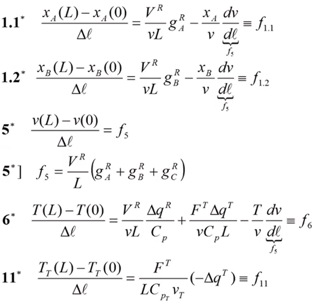
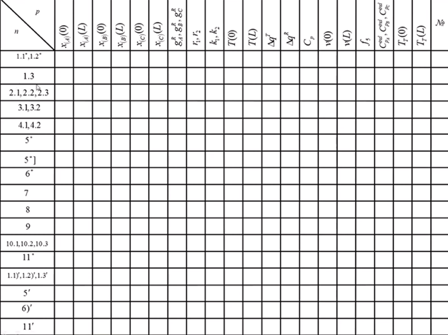
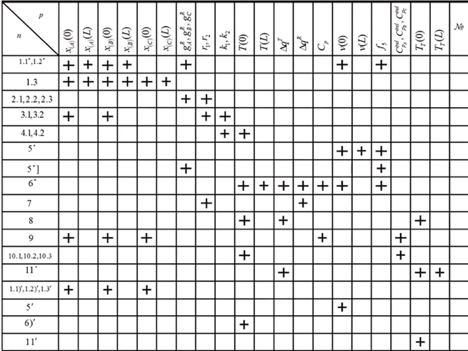
Начальные условия:

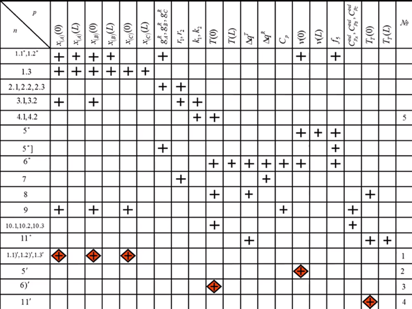
Расчёты:

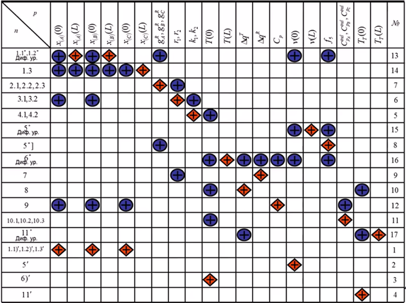
Блок-схема:

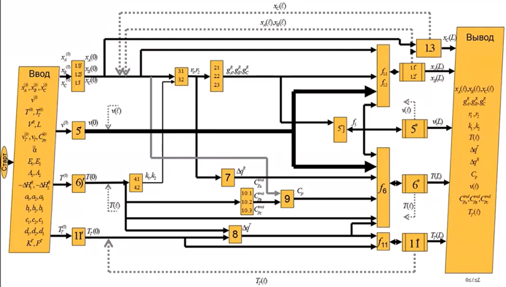
Итерации идут по длине. Их столько же, сколько и начальных условий. Когда заканчивается длина трубы, значит, величины уже выходные.

13. Математическое описание стационарного гомогенного процесса в проточном трубчатом реакторе с рубашкой (теплоноситель движется в режиме противотока) с конкретной стехиометрией реакции. Выбор алгоритма решения прямой задачи моделирования с применением информационной матрицы системы уравнений математического описания. Блок-схема алгоритма решения задачи моделирования.

Построение математической модели стационарного режима процесса с противоточным движением теплоносителя (решение краевой задачи):

Первые 2 уравнения – определение для определения ключевых компонентов.

Хс выражается через 2 ключевых компонента.

х_С^((0))- начальное условие, х_С – текущее значение С через концентрации А и В.

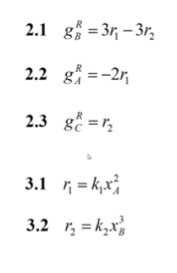
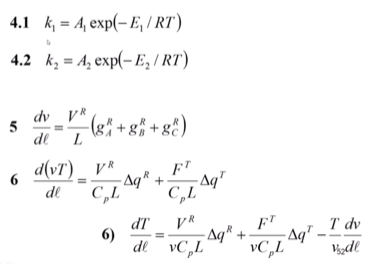
5 – определение скорости движения по длине реактора. Ур-ие общего материального баланса

Если будет реактор аддиабатический, то 6 уравнения нет.

6 – уравнение теплового баланса в реакторе - изменение температуры по длине.

7 – определение изменения локального тепла за счёт химической реакции.

8 – локальное изменение тепла за счёт теплопередачи. К^Т – константа теплопередачи.

9 – общее значение теплоёмкости.

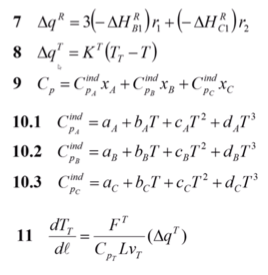
10 – индивидуальные значения теплоёмкостей.

11 – тепловой баланс теплоносителя. ∆q^T – нет знака минуса

Для определения частного решения системы обыкновенных дифференциальных уравнений необходимо решить краевую задачу, при этом задаются следующие начальные условия:

Задание начальных условий и изменение концентраций компонентов, расхода потока и температур реакционного и вспомогательного (теплового) потоков по длине реактора:

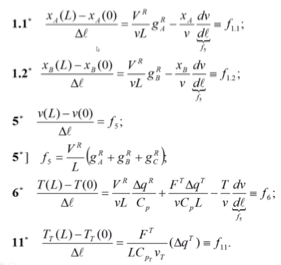
Начальные условия:

Расчеты:

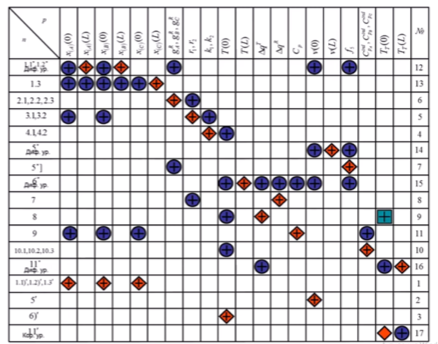
Блок схема:

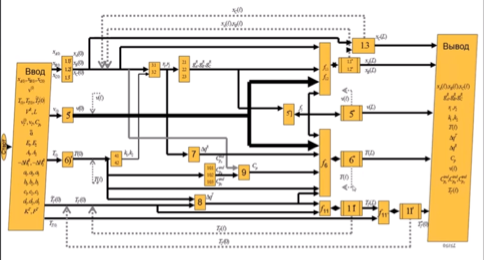
14. Математическое описание нестационарного гомогенного изотермического процесса в проточном трубчатом реакторе с простейшей стехиометрией реакции A-P. Выбор способа дискретизации системы дифференциальных уравнений с частными производными. Начальные и граничные условия задачи моделирования. Алгоритм решения прямой задачи моделирования.

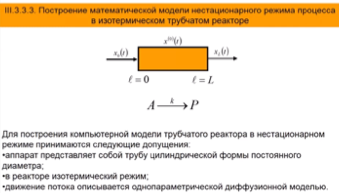
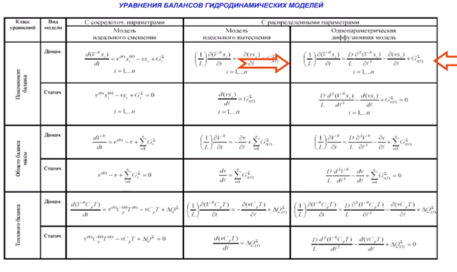
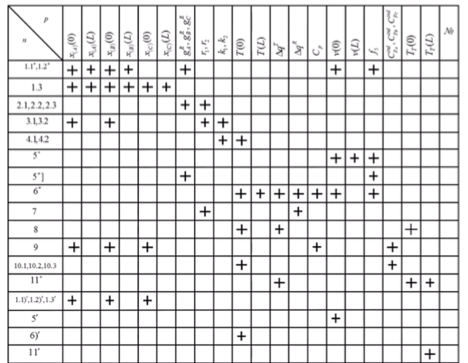
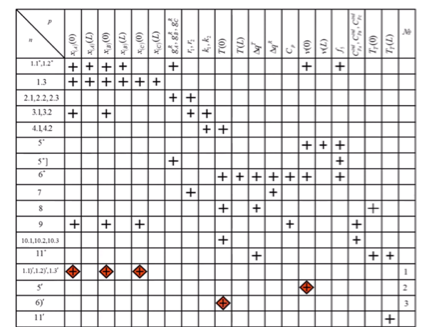
Таблицу можно использовать на зачете!

Уравнение записывается по времени и по длине и получается дифф. Ур-ие с частными производными.

Маленькая v- линейная скорость потока.

S – диаметр.

Делим переменные:

ТОЖЕ САМОЕ, НО В МАТРИЧНОМ ВИДЕ

15. Теоретические физико-химические и эмпирические регрессионные модели химико-технологических процессов. Прямые и обратные задачи построения математических моделей и алгоритмы их решения. Структурная и параметрическая идентификация математических моделей. Анализ параметрической чувствительности процессов. Постановка и решение задачи оптимизации. Инструменты для решения задач компьютерного моделирования – пакеты компьютерной математики (ПКМ) и пакеты моделирующих программ (ПМП).

Несмотря на большое разнообразие подходов к моделированию химико-технологических систем, таких как, например, применение конечных автоматов, вероятностных марковских процессов, нейронных сетей, доминирующими остаются в настоящее время два подхода: теоретическое физико- химическое и эмпирическое регрессионное моделирование. Первый подход основан на знании механизмов протекающих процессов и на блочном принципе построения полной модели, а второй – на обработке большого объема экспериментальной информации о входных и выходных параметрах процесса и базируется на кибернетическом принципе «черного ящика» и применении методов регрессионного, корреляционного и дисперсионного анализа при построении моделей.

На практике достаточно часто эти подходы приходится совмещать, так как математические физико-химические модели не всегда применимы для описания процессов на отдельных ступенях иерархии (для отдельных блоков) полной системы.

Необходимо подчеркнуть, что в настоящее время стремление к разработке теоретических физико-химических блочных математических моделей химикотехнологических процессов преобладает, а регрессионные модели используются, когда знаний о теории и механизме протекающих процессов недостаточно.

При этом процесс моделирования можно представить в виде следующих этапов:

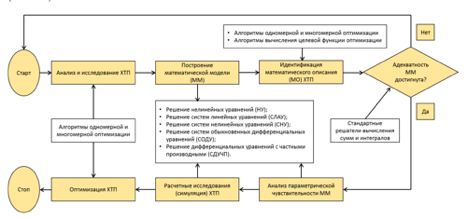
Рис. Блок-схема процедуры компьютерного моделирования ХТП

Активный эксперимент проводится по заранее составленному плану, в

соответствии с которым ставится задача не только определения оптимальных

условий проведения эксперимента, но и оптимизации процесса (оптимальное

планирование эксперимента).

Для структурной и параметрической идентификации математического описания процесса необходимы алгоритмы одномерной и многомерной оптимизации для определения параметров (коэффициентов) моделей, а также алгоритмы вычисления целевой функции оптимизации в виде суммы или интеграла, оценивающих согласование расчетных и экспериментальных данных.

Для решения оптимизационных задач необходимо :

1. Выбрать или сформировать целевую функцию 𝑅 = 𝑅(𝑥̅) – критерий оптимальности, который должен быть количественным, чувствительным (по возможности заметно изменяться в зависимости от изменения ресурсов оптимизации – оптимизирующих переменных), и иметь экстремальное (минимальное или максимальное) значение в рассматриваемом интервале решения задач.

2. Выявить обоснованные ресурсы оптимизации – оптимизирующие переменные 𝑥̅, влияющие на целевую функцию R и позволяющие обеспечить ее экстремальный характер.

3. Располагать надежным алгоритмом оптимизации, реализованным в данном случае в виде стандартного решателя MATLAB, для определения оптимального решения – в общем случае оптимального значения ресурса оптимизации – оптимизирующих переменных 𝑥̅ 𝑜𝑝𝑡 и экстремальной (минимальной или максимальной) величины целевой функции – критерия оптимальности 𝑅 𝑜𝑝𝑡 .

Одним из важнейших преимуществ ПКМ является их относительно простое усвоение и обучение работе с ними специалистов в разнородных предметных областях, не являющихся профессиональными программистами. Практически все алгоритмы решения типичных задач вычислительной математики представлены в них в виде решателей, для применения которых специалисту или научному работнику необходимо на используемом ПКМ языке программирования записать функцию, соответствующую постановке решаемой им технической или научной задачи. Для применения пакетов компьютерной математики инженеру необходимо изучить язык программирования, встроенный в ПКМ, и научиться пользоваться решателями для решения собственных математических задач.

Некоторые решатели ПКМ MATLAB, используемые для реализации численных методов вычислительной математики при компьютерном моделировании ХТП.

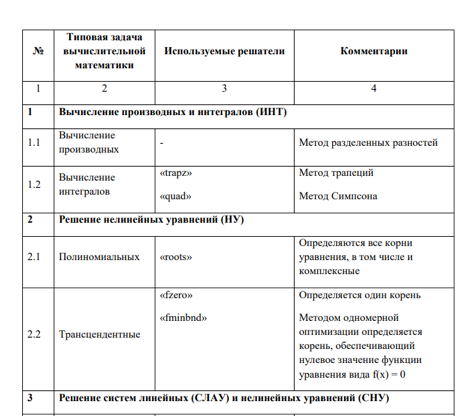
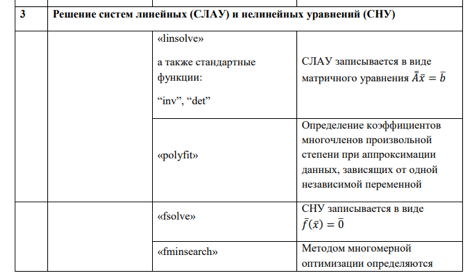
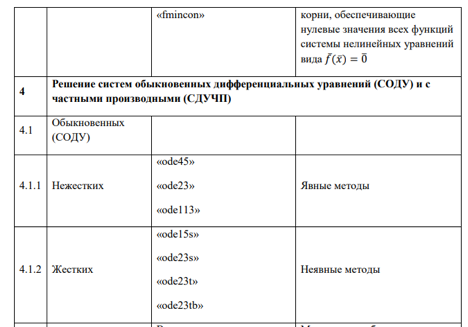
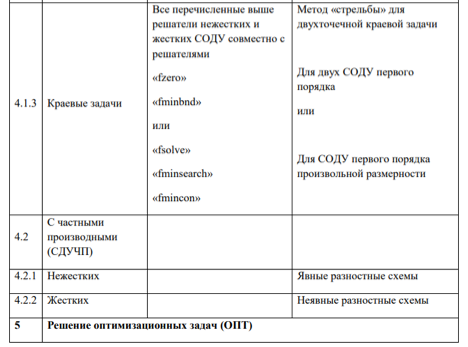
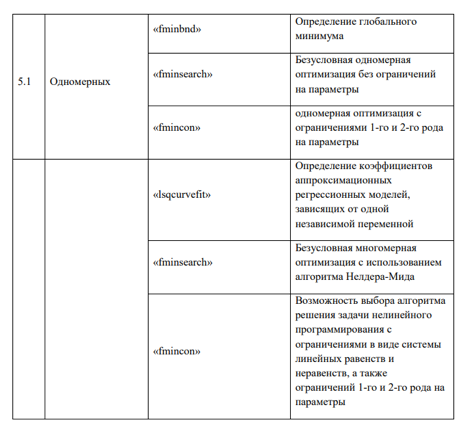
В общем случае с применением современных ПМП -- симуляторов химических производств -- решаются следующие задачи:

• * анализа, оптимизации и синтеза химико-технологических систем (ХТС) для проектируемых и действующих производств

• * исследования динамического поведения ХТС для синтеза систем управления;

• * разработки компьютерных систем обучения операторов химических производств, в частности тренажёрных комплексов.

Большинство систем моделирования включает набор следующих основных подсистем, обеспечивающих решение задачи моделирования химико-технологических процессов:

• набор термодинамических данных по чистым компонентам (база данных) и средства, позволяющие выбирать определенные компоненты для описания качественного состава рабочих смесей;

• средства представления свойств природных углеводородных смесей, главным образом - нефтей и газоконденсатов, в виде, приемлемом для описания качественного состава рабочих смесей, по данным лабораторного анализа;

• различные методы расчета термодинамических свойств, таких как коэффициент фазового равновесия, энтальпия, энтропия, плотность, растворимость газов и твердых веществ в жидкостях и фугитивность паров;

• набор моделей для расчета отдельных элементов технологических схем процессов;

• средства для формирования технологических схем из отдельных элементов;

• средства для расчета технологических схем, состоящих из большого числа элементов, определенным образом соединенных между собой.

16. Построение моделей линейной и нелинейной регрессии. Основные допущения регрессионного анализа. Определение коэффициентов математических моделей в случае линейной и нелинейной регрессии. Оценка погрешностей регрессионных уравнений.

Регрессионный анализ позволяет:

производить расчет регрессионных моделей путем определения значений параметров — постоянных коэффициентов при независимых переменных — регрессорах, которые часто называют факторами;

проверять гипотезу об адекватности модели имеющимся наблюдениям;

использовать модель для прогнозирования значений зависимой переменной при новых или ненаблюдаемых значениях независимых переменных.

Уравнение регрессии адекватно реальному моделируемому явлению или процессу только в случае соблюдения требований его построения:

1. Совокупность исходных данных должна быть однородной и математически описываться непрерывными функциями.

2. Наличие достаточно большого объема исследуемой выборочной совокупности.

3. Возможность описания моделируемого явления одним или несколькими уравнениями причинно-следственных связей.

4. Причинно-следственные связи между явлениями и процессами, по возможности, следует описывать линейной (или приводимой к линейной) формой зависимости.

5. Отсутствие количественных ограничений по параметрам модели.

6. Количественное выражение факторных признаков.

7. Постоянство структуры изучаемой совокупности в пространстве и во времени.

Проверить значимость оценок коэффициентов регрессии — значит установить, достаточна ли величина оценки для статистически обоснованного вывода о том, что коэффициент регрессии отличен от нуля. Для этого проверяют гипотезу о равенстве нулю коэффициента регрессии, соблюдая предпосылки «нормальной регрессии». В этом случае вычисляемая для проверки нулевой гипотезы статистика

имеет распределение Стьюдента с к= n-2 степенями свободы (b — оценка коэффициента регрессии, — оценка среднеквадратического отклонения коэффициента регрессии, иначе стандартная ошибка оценки). По уровню значимости а и числу степеней свободы к находят по таблицам распределения Стьюдента критическое значение удовлетворяющее условию то нулевую гипотезу о равенстве нулю коэффициента регрессии отвергают, коэффициент считают значимым. Принет оснований отвергать нулевую гипотезу.

Оценки среднеквадратического отклонения коэффициентов регрессии вычисляют по следующим формулам:

где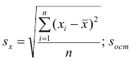 — оценка остаточной дисперсии.

Доверительный интервал для значимых параметров строят по обычной схеме. Из условия

где а — уровень значимости, находим

17. Пассивный эксперимент и обработка его результатов методом регрессионного анализа. Выбор уравнений для описания экспериментальных данных. Определение коэффициентов регрессии. Оценка значимости коэффициентов и определение адекватности математических моделей.

Ответ:

Приближенные уравнения регрессии в общем виде:

Для определения конкретного вида приближенного уравнения регрессии необходимо:

1) Найти конкретный вид функции f, в частности, линейна или не линейна она относительно коэффициентов ;

2) Определить значения коэффициентов модели – коэффициентов регрессии;

3) Провести статический анализ полученных результатов.

Статический анализ, как правило, проводится методами регрессионного и корреляционного анализа.

В общем случае различают два вида уравнений регрессии (эмпирических моделей) – нелинейные по параметрам , статистический анализ которых осуществляется методом «нелинейной регрессии» и линейные по параметрам , статистический анализ которых проводится методом «линейной регрессии».

Линейные по параметрам модели могут быть представлены в следующем виде:

где - линейные или нелинейные функции входных переменных ().

Определение параметров (коэффициентов) линейных моделей и их регрессионный анализ существенно проще, чем для нелинейных моделей.

Поэтому нелинейные модели, по возможности, стараются линеаризовать и привести к виду (6).

Частными случаями уравнения линейной регрессии являются:

А) полиномиальная регрессия, когда

и её разновидности – линейная регрессия от одной переменной (m=1 ):

и параболическая регрессия (m=2 ):

Б) трансцендентная регрессия и её разновидности в виде зависимости показательного типа:

которая линеаризуется логарифмически:

и дробно-показательного типа:

+которая также линеаризуется логарифмически:

В) множественная регрессия, когда число входных переменных больше 1:

Для определения коэффициентов линейной или линеаризованной регрессионной модели необходимо выполнить следующую последовательность действий:

· сформировать вектор наблюдений и вычислить его компоненты (только для линеаризованных моделей);

· сформировать и рассчитать компоненты матрицы, зависящей от входных переменных; транспонировать матрицу ;

· перемножить транспонированную матрицу на исходную матрицу ;

· выполнить обращение информационной матрицы - ;

· умножить полученную обратную матрицу на матрицу ;

· умножить полученный результат на вектор наблюдений и получить выборочные коэффициенты регрессии .

Определение значимости коэффициентов регрессии. (Выполнение второго этапа регрессионного анализа).

Для этого используется нормированная случайная величина: подчиняющаяся t –распределению Стьюдента. Воспользовавшись оценкой дисперсии из (49) и , можно записать вероятностное соотношение: В этом случае табличное значение t берётся при доверительной вероятности β (чаще всего 0,95) и числе степеней свободы дисперсии воспроизводимости (48) – f_e . Если предположить, что математическое ожидание коэффициента (т.е. истинное его значение равно нулю), то условие незначимости коэффициента a_j имеет вид (62): Для значимых коэффициентов в соответствии с (62), раскрывая неравенство, получим следующий доверительный интервал: Это означает, что вместо оценки коэффициентов регрессии можно пользоваться их крайними значениями в соответствии с (64). Это в свою очередь приведёт к различным величинам в уравнении: В результате на графике вместо одной кривой, полученной по оценочным значениям коэффициентов регрессии, получается три: одна - минимальных значений a_j , вторая – максимальных значений a_j и третья – сплошная, для оценочных значений коэффициентов регрессии:

Проверка адекватности уравнения регрессии - математической модели. (Выполнение третьего этапа регрессионного анализа).

В результате успешного решения задачи идентификации (параметрической и структурной) должна получиться адекватная математическая модель (ММ). Под адекватностью ММпонимается:

1) Качественное и количественное соответствие поведения ММ и объекта моделирования.

2) Выполнение этого соответствия как при одном наборе режимных параметров (адекватность состояния), так и при различных наборах режимных параметров (адекватность поведения).

3) Возможность интерполяции и экстраполяции свойств реального объекта с помощью ММ.

18. Активный полный факторный эксперимент (ПФЭ) и обработка его результатов. Выбор уравнений для описания экспериментальных данных. Определение коэффициентов регрессии. Оценка значимости коэффициентов и определение адекватности регрессионных моделей.

Ответ:

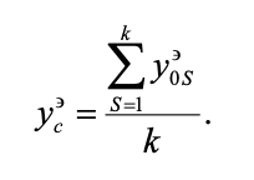
19. Ортогональное центральное композиционное планирование экспериментов (ОЦКП) и обработка его результатов. Выбор уравнений для описания экспериментальных данных. Определение коэффициентов регрессии. Оценка значимости коэффициентов и определение адекватности регрессионных моделей.

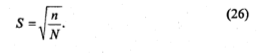
n – число экспериментов ПФЭ

N – общее число опытов ОЦКП

S – дисперсия, вычисляется, чтобы обеспечить ортогональность матрицы Ф

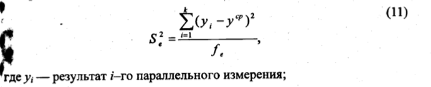
f_e – число степеней свободы

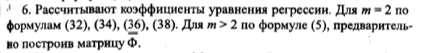
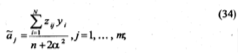
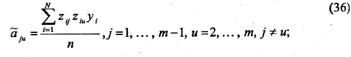
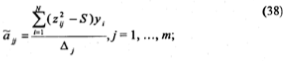
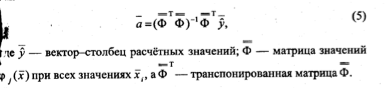
S^2_e - дисперсия воспроизводимости