
1й курс / Konspekt_lektsiy_Informatika_7
.pdf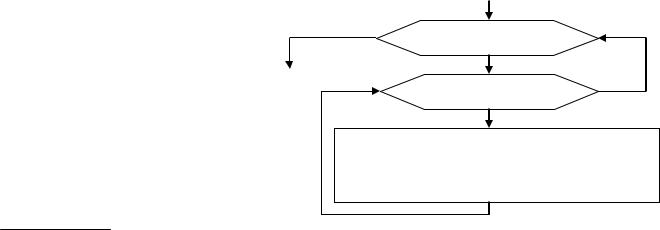
1
Тема №8. АЛГОРИТМИЗАЦИЯ И С++. ДВУМЕРНЫЕ МАССИВЫ
8.1. Описание двумерных массивов
Двумерный массив (матрица) представляет собой таблицу, на пересечении строк и столбцов которой располагаются элементы. Каждый элемент имеет два индекса. Первый индекс обычно обозначается буквой i и указывает номер строки, в которой расположен элемент. Второй индекс обозначается буквой j и указывает номер столбца, в котором расположен элемент. В С++ нумерация строк и столбцов матрицы начинается с 0.
Номера столбцов
j=0 |
j=1 |
j=2 |
... |
j=N–1 |
Номера строк
i=0 |
A0,0 |
A0,1 |
A0,2 |
... |
A0,N–1 |
|
|
|
|
|
|
i=1 |
A1,0 |
A1,1 |
A1,2 |
... |
A1,N–1 |
|
|
... |
... |
Ai,j |
... |
... |
… |
||||
|
|
|
|
|
|
|
|
|
|
|
|
i=M–1 |
AM–1,0 |
AM–1,1 |
AM–1,2 |
... |
AM-1,N–1 |
|
|
|
|
|
|
Основные характеристики двумерного массива:
1)размерность – задается двумя числами: количество строк и количество столбцов;
2)значения и тип элементов массива.
Двумерный массив, у которого количество строк равно количеству столбцов называется
квадратной матрицей, в противном случае – прямоугольной.
Структура описания двумерного массива в С++:
тип имя_матрицы [M][N];
где M – количество строк (нумеруются от 0 до M–1);
N – количество столбцов (нумеруются от 0 до N–1). Например,
int A[10][15]; //Описана целочисленная матр. A, состоящая из 10 строк и 15 столбцов
Для доступа к значению, хранящемуся в определенном элементе двумерного массива (для обращения к элементу массива), необходимо указать имя массива и последовательно индексы этого элемента.
Например, A[2][3].
В С++ можно использовать многомерные массивы, которые описываются следующим образом:
тип имя_массива [M1][M2]…[Mk];
Для обработки двумерного массива требуетсядва вложенных цикла, при этом наиболее удобно использовать циклы«Для» на основе блока модификации. Один цикл будет перебирать номера строк, второй – но-  мера столбцов массива. Таким образом, будут перебраны все элементы двумерного массива.
мера столбцов массива. Таким образом, будут перебраны все элементы двумерного массива.
В общем видеалгоритм обра-  ботки двумерного массива выглядит следующим образом:
ботки двумерного массива выглядит следующим образом:
Внешний цикл (по параметру i) при i = 0 «выбирает» 0-ю строку массива. Внутренний цикл (по параметру j) перебирает номера столбцов массива от 0 до N–1, т.е. в теле внутреннего
ÓЕфименко К.Н.

2
цикла поочередно выбираются элементы A0,0, А0,1, А0,2 и т.д. до конца 0-й строки. После выхода из внутреннего цикла происходит возврат во внешний цикл, где выбирается 1-я строка массива, для которой внутренний цикл опять переберет поочередно все элементыA1,0, А1,1, А1,2 и т.д. Та-
ким образом, элементы двумерного массива будут перебираться по строкам.
Если в блок-схеме алгоритма поменять местами параметры внешнего и внутреннего циклов, т.е. внешний цикл сделать по параметру j, а внутренний – по параметру i, то элементы массива будут перебираться по столбцам.
8.2. Ввод-вывод элементов двумерного массива
Ввод двумерного массива, также как и одномерного выполняется в два этапа. Вначале задается его размерность, а затем вводятся значения для каждого элемента массива.
Блок-схема алгоритма ввода двумерного массива:
Ввод M,N
i=0; i<M; i++
j=0; j<N; j++
Ввод Ai,j
Варианты ввода двумерного массива:
Вариант 1. Ввод массива с помощью функции scanf.
…
float a[10][10]; int i,j,m,n;
printf("\n M="); scanf("%d",&m); printf("\n N="); scanf("%d",&n); for(i=0; i<m; i++)
for(j=0; j<n; j++)
{printf("A[%d][%d]=",i,j);
scanf("%f",&a[i][j]);
}
…
Вариант 2. Ввод массива с помощью оператора cin.
…
float a[10][10]; int i,j,m,n;
cout<<"\n M="; cin>>m; cout<<"\n N="; cin>>n; for(i=0; i<m; i++) for(j=0; j<n; j++)
{
cout<<"A["<<i<<"]["<<j<<"]=";
cin>>a[i][j];
}
Вывод двумерного массива также выполняется поэлементно с помощью вложенных циклов «Для».
ÓЕфименко К.Н.

3
Блок-схема алгоритма вывода двумерного массива:
i=0; i<M; i++
j=0; j<N; j++
Вывод Ai,j
Варианты вывода двумерного массива в виде таблицы:
Вариант 1. Вывод массива с помощью функции printf.
…
for(i=0; i<m; i++)
{
for(j=0; j<n; j++) printf("A[%d][%d]=%f\t",i,j,a[i][j]); printf("\n");
}
…
Вариант 2. Вывод массива с помощью оператора cin.
…
for(i=0; i<m; i++)
{
for(j=0; j<n; j++) cout<<"A["<<i<<"]["<<j<<"]="<<a[i][j]<<"\t";
cout<<endl;
}
…
Пример 8.1. В двумерном массиве А[M,N], состоящем из вещественных чисел найти минимальный положительный элемент.
Принцип поиска максимального (минимального) элемента в двумерном массиве аналогичен принципу, используемому для одномерного массива. Только в качестве параметров такого элемента определяются номера строки и столбца.
int main()
{float a[10][10]; int i,j,m,n,im,jm;
cout<<"\n M="; cin>>m; cout<<"\n N="; cin>>n; for(i=0; i<m; i++)
for(j=0; j<n; j++)
{cout<<"A["<<i<<"]["<<j<<"]="; cin>>a[i][j]; }
im=-1;
for(i=0; i<m; i++) for(j=0; j<n; j++) if (a[i][j]>0)
if (im==-1) {im=i; jm=j;}
else if (a[i][j]<a[im][jm]){im=i; jm=j;} if (im!=-1)
cout<<"Min=A["<<im<<","<<jm<<"]="<<a[im][jm]; else
ÓЕфименко К.Н.

cout<<"Net elementov >0\n";
}
НАЧАЛО
Ввод M,N
i=0; i<M; i++
im = –1 |
j=0; j<N; j++ |
Ввод Ai,j
i=0; i<M; i++
–
im ≠ –1 |
|
|
j=0; j<N; j++ |
|
|
|
|
||
+ |
|
– |
||
|
|
|||
Вывод |
|
|
Ai,j > 0 |
|
|
|
|
|
|
Aim,jm |
|
+ |
|
|
|
|
– |
||
|
|
|
im = –1 |
|
КОНЕЦ |
– |
+ |
|
|
|
|
|||
|
|
Ai,j<Aim,jm |
||
|
|
|
|
|
|
|
|
im = i |
|
|
|
|
jm = j |
|
|
|
|
|
|
4
+
im = i jm = j
Пример 8.2. В двумерном массиве А[M,N], состоящем из вещественных чисел определить среднее арифметическое значение отрицательных элементов.
…
int k=0; float s=0; for(i=0; i<m; i++) for(j=0; j<n; j++)
if (a[i][j]<0) {k++; s+=a[i][j];} if (k!=0)
cout<<"Average A[i,j]<0 = "<<s/k<<endl; else
cout<<"Net elementov <0\n";
…
ÓЕфименко К.Н.

5
8.3. Задачи на обработку двумерного массива
Дана матрица A[4;4]
a00 |
a01 |
a02 |
a03 |
a10 |
a11 |
a12 |
a13 |
a20 |
a21 |
a22 |
a23 |
a30 |
a31 |
a32 |
a33 |
i < j |
i = j |
i > j |
i<N-j-1 |
i=N-j-1 |
i>N-j-1 |
Главной диагональю квадратной матрицы называется диагональ, соединяющая верхний левый угол матрицы с правым нижним углом. Для элементов, расположенных на главной диагонали соблюдается соотношение между индексами: i = j. Для элементов расположенных ниже главной диагонали: i > j. Для элементов расположенных выше главной диагонали: i < j.
Побочной диагональю квадратной матрицы называется диагональ, соединяющая нижний левый угол матрицы с правым верхним углом. Для элементов, расположенных на побочной диагонали соблюдается соотношение между индексами: i = N–j–1. Для элементов расположенных ниже побочной диагонали: i > N–j–1. Для элементов расположенных выше – i < N–j–1.
ЗАДАЧА 1. Найти сумму элементов квадратной матрицы А[N,N], расположенных выше
главной диагонали.
НАЧАЛО
a00 |
|
a01 |
a02 |
a03 |
|
a10 |
a11 |
a12 |
a13 |
Ввод N |
|
a 20 |
a21 |
a 22 |
a23 |
|
|
a30 |
a31 |
a32 |
a33 |
|
|
|
|||||
|
|
i=0; i<N; i++ |
|
|
|
|
|
S = 0 |
j=0; j<N; j++ |
||
|
|
Ввод Ai,j |
|
|
|
|
|
|
|
i=0; i<N; i++ |
|
int main() |
|
|
|
{float a[10][10],s; |
|
j=0; j<N; j++ |
|
int i,j,n; |
Вывод S |
|
|
cout<<"\n N="; |
|
+ |
|
cin>>n; |
– |
||
for(i=0; i<n; i++) |
КОНЕЦ |
i < j |
|
|
|
||
for(j=0; j<n; j++) |
|
|
S = S + Ai,j |
{ cout<<"A["<<i<<"]["<<j<<"]="; |
|
|
|
cin>>a[i][j]; } |
|
|
|
s=0; |
|
|
|
for(i=0; i<n; i++) |
|
|
|
for(j=0; j<n; j++) |
|
|
|
ÓЕфименко К.Н.

|
6 |
|
if (i<j) s+=a[i][j]; |
|
|
cout<<"S = "<<s<<endl; |
|
|
S = 0 |
|
|
} |
|
|
Для перебора только элементов квад- |
|
|
ратной матрицы расположенных выше глав- |
i=0; i<N-1;i++ |
|
ной диагонали достаточно организовать два |
|
|
вложенных цикла со следующими парамет- |
|
|
рами: i = 0 ¸ N–2 и j = i+1 ¸ N–1. Аналогично |
j=i+1; j<N;j++ |
|
для перебора элементов расположенных ниже |
|
|
главной диагонали – i = 1 ¸ N–1 и j = 0 ¸ i–1. |
|
|
S = S + Ai,j |
|
|
Для перебора только элементов квад- |
|
|
ратной матрицы расположенных выше - по |
|
|
|
|
|
бочной диагонали достаточно организовать два вложенных цикла со следующими параметрами: i = 0 ¸ N–2 и j = 0 ¸ N–i–2. Аналогично для перебора элементов расположенных ниже побочной диагонали – i = 1 ¸ N–1 и j = N–i ¸ N–1.
ЗАДАЧА 2. Поменять местами максимальные элементы главной и побочной диагоналей квадратной матрицы А[N,N].
Для перебора элементов, расположенных на главной или побочной диагонали достаточно организовать только один цикл по параметруi = 0 ¸ N–1, и обращаться к элементу главной диагонали – Ai,i, к элементу побочной диагонали – Ai,N–i–1.
|
|
|
|
a00 |
a01 |
a02 |
a00 |
a01 |
a02 |
a03 |
|
|
im1 = 0 |
|
|
||||||||
|
|
|
a10 |
a11 |
a12 |
a13 |
|||||
|
im2 = 0 |
|
|
a10 |
a11 |
a12 |
|||||
|
|
|
|
a20 |
a21 |
a22 |
a20 |
a21 |
a22 |
a23 |
|
|
|
|
|
||||||||
|
i=1; i<N; i++ |
|
|
|
|
|
a30 |
a31 |
a32 |
a33 |
|
|
|
|
|
|
|
im1≠N-im2-1 |
|
– |
|
|
|
|
Ai,i>Aim1,im1 |
+ |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
+ |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
– |
im1 = i |
|
|
|
|
|
|
|
|
|
|
b = Aim1,im1 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
||||||
|
|
|
|
|
Aim1,im1 = Aim2,N-im2-1 |
|
|
|
|
||
– |
|
|
Aim2,N-im2-1 = b |
|
|
|
|
||||
Ai,N-i-1>Aim2,N-im2-1 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|||
+
im2 = i
…
im1=0;im2=0; for(i=1; i<n; i++)
{
if (a[i][i]>a[im1][im1]) im1=i;
if (a[i][n-i-1]>a[im2][n-im2-1]) im2=i;
}
if (im1!=n-im2-1) {b=a[im1][im1]; a[im1][im1]=a[im2][n-im2-1]; a[im2][n-im2-1]=b;}
ÓЕфименко К.Н.
7
else
cout<<"Max elements are the same!"<<endl;
…
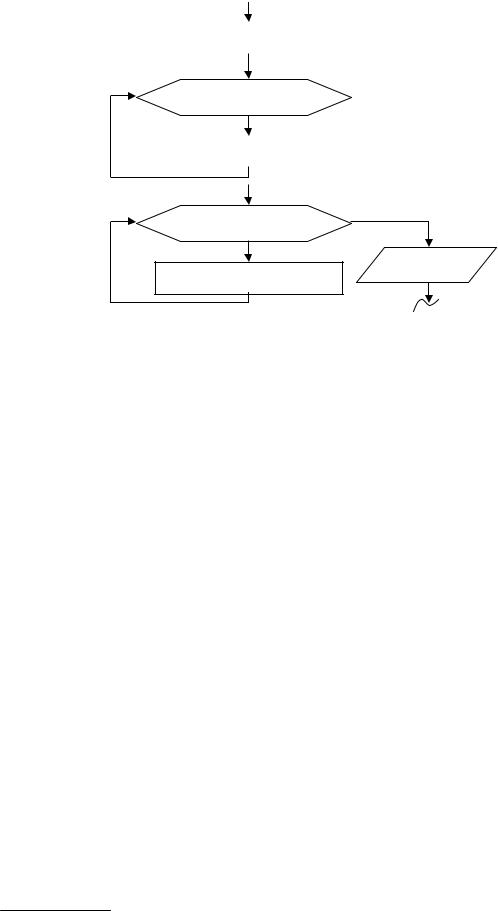
ЗАДАЧА 3. Вычислить сумму элементов квадратной матрицы А[N,N], расположенных по ее периметру. 
|
S = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a 00 |
|
a 01 |
a 02 |
|
a 03 |
|||
|
|
|
|
|
|
|
a10 |
|
|
|
|
a13 |
|
|
|
|
|
|
|
|
a11 |
a12 |
|
||
|
|
|
|
|
|
|
|
|
||||
|
i=0; i<N;i++ |
|
|
a 20 |
|
a 21 |
a 22 |
a 23 |
||||
|
|
|
||||||||||
|
|
|
|
|
|
|
a 30 |
|
a 31 |
a 32 |
|
a 33 |
S = S + Ai,0 + Ai,N–1 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j=1; j<N-1;j++
Вывод S
S = S + A0,j + AN–1,j
ЗАДАЧА 4. Преобразовать матрицу A[M,N] так, чтобы строки с нечетными индексами были упорядочены по убыванию, c четными – по возрастанию.
…
for(i=0; i<m; i++) if ((i%2)==0)
{ for(k=0; k<n-1; k++) for(j=0; j<n-k-1; j++)
if (a[i][j]>a[i][j+1])
{b=a[i][j];
a[i][j]=a[i][j+1]; a[i][j+1]=b; }
}
else
{ for(k=0;k<n-1;k++) for(j=0;j<n-k-1;j++)
if (a[i][j]<a[i][j+1])
{b=a[i][j];
a[i][j]=a[i][j+1]; a[i][j+1]=b; }
}
…
ЗАДАЧА 5. Сформировать вектор В[M], каждый элемент которого равен количеству нулевых элементов соответствующей строки целочисленной матрицы А[M,N].
int main()
{int a[10][10],b[10]; int i,j,m,n; cout<<"\nM="; cin>>m; cout<<"N="; cin>>n; for(i=0; i<m; i++) for(j=0; j<n; j++)
{cout<<"A["<<i<<"]["<<j<<"]="; cin>>a[i][j]; }
ÓЕфименко К.Н.

8
for(i=0; i<m; i++) |
НАЧАЛО |
|
{ b[i]=0; |
||
|
||
for(j=0; j<n; j++) |
|
|
if (a[i][j]==0) b[i]++; |
Ввод M, N |
|
cout<<"B["<<i<<"]="<<b[i]<<endl; |
|
|
} |
|
|
} |
|
i=0; i<M; i++
j=0; j<N; j++
Ввод Ai,j
i=0; i<M; i++ |
|
|
||||
|
|
|
|
|
Вывод Bi |
|
КОНЕЦ |
|
Bi = 0 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j=0; j<N; j++ |
|
|
||||
– |
+ |
|
|
|||
|
|
Ai,j = 0 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
Bi = Bi + 1 |
|
|
|
|
|
||||
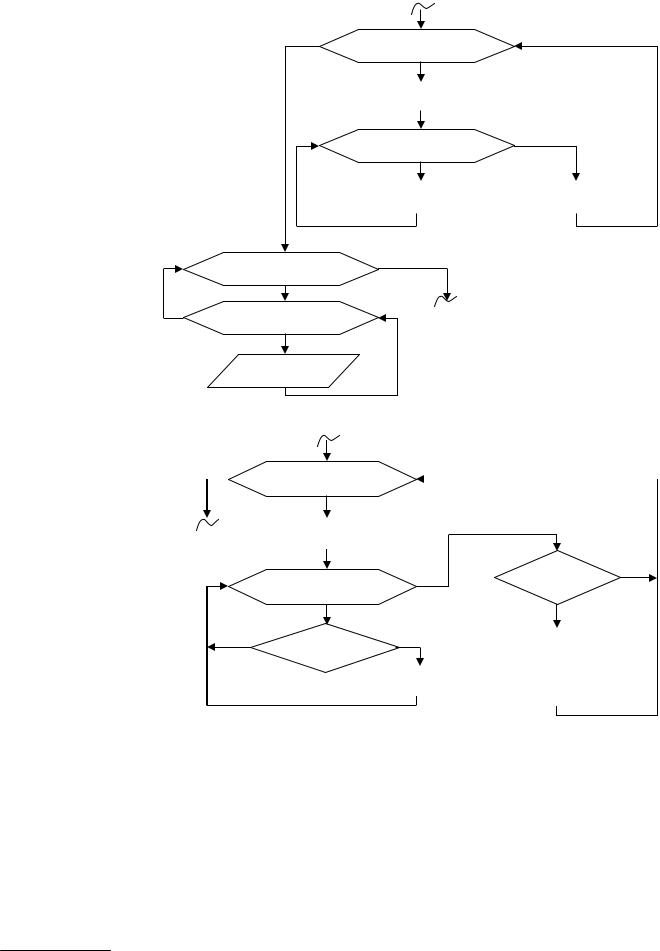
ЗАДАЧА 6. Сформировать вектор В[N], каждый элемент которого равен среднему |
||||||
арифметическому значению положительных элементов |
соответствующего |
столбца матрицы |
||||
А[M,N]. |
|
|
|
|
|
|
j=0; j<N; j++
Bj = 0 k=0
–
k ≠ 0
i=0; i<M; i++
+
… |
– |
Ai,j > 0 |
|
for(j=0; j<n; j++) |
|
{b[j]=0; k=0; |
|
for(i=0; i<m; i++) |
|
if (a[i][j]>0) |
|
{b[j]+=a[i][j]; k++;} |
|
if (k!=0) b[j]=b[j]/k; |
|
cout<<"B["<<j<<"]="<<b[j]<<endl;
}…
+ |
Bj = Bj/k |
|
Bj = Bj + Ai,j |
Вывод Bj |
k = k + 1 |
ÓЕфименко К.Н.
9
ЗАДАЧА 7. Преобразовать исходную матрицу A[M,N] так, чтобы первый элемент каждого столбца был заменен средним арифметическим последующих элементов этого же столбца.
… |
|
|
|
|
|
|
for(j=0; j<n; j++) |
|
j=0; j<N; j++ |
|
|
|
|
{ |
|
|
|
|
|
|
s=0; |
|
|
|
|
|
|
|
|
S = 0 |
|
|
|
|
for(i=1; i<m; i++) |
|
|
|
|
|
|
s+=a[i][j]; |
|
|
|
|
|
|
a[0][j]=s/(m-1); |
|
i=1; i<M; i++ |
|
|
|
|
} |
|
|
|
|
|
|
for(i=0; i<m; i++) |
|
|
|
|
|
|
{for(j=0; j<n; j++) |
|
|
S = S + Ai,j |
|
|
A0,j = S/(M–1) |
cout<<"A["<<i<<"]["<<j |
|
|
|
|
|
|
|
|
|
|
|
|
|
<<"]="<<a[i][j]<<"\t"; |
|
|
|
|||
cout<<endl;} |
|
|
|
|
|
|
… |
i=0; i<M; i++ |
|
|
|
||
j=0; j<N; j++
Вывод Ai,j
ЗАДАЧА 8. В каждой строке матрицы А[N,N] найти наибольший элемент и поменять его местами с элементом главной диагонали.
|
|
i=0; i<N; i++ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
jm = 0 |
|
|
|
|
|
|
|
|
|
|
|
– |
|
|
|
|
|
|
|
|
|
|
j=1; j<N; j++ |
|
|
i ≠ jm |
||
|
|
|
|
|
|
||
|
|
|
|
|
|
+ |
|
… |
|
– |
+ |
|
|
|
|
|
b = Ai,i |
|
|||||
for(i=0; i<n; i++) |
|
Ai,j > Ai,jm |
|
|
|
||
|
|
|
|
Ai,i = Ai,jm |
|
||
{ |
jm=0; |
|
|
jm = j |
|
Ai,jm = b |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
for(j=1; j<n; j++) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
if (a[i][j]>a[i][jm]) jm=j; |
|
|
|
|
||
|
if (i!=jm) |
|
|
|
|
|
|
{b=a[i][i];
a[i][i]=a[i][jm]; a[i][jm]=b; }
}
for(i=0; i<n; i++)
{
for(j=0; j<n; j++) cout<<"A["<<i<<"]["<<j<<"]="<<a[i][j]<<"\t"; cout<<endl;
}…
ÓЕфименко К.Н.
