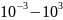Метрология_ЛР3(8)_Обработка
.docxМИНОБРНАУКИ РОССИИ
Санкт-Петербургский государственный
электротехнический университет
«ЛЭТИ» им. В.И. Ульянова (Ленина)
Кафедра информационно-измерительных систем и технологий
отчет
по лабораторной работе №8
по дисциплине «Метрология»
Тема: Измерение параметров электрических цепей
Студенты гр. 1585 |
|
Левшин С.Ю. |
|
|
Хватов А.В. |
|
|
|
Преподаватель |
|
Царёва А.В. |
Санкт-Петербург
2023
Цель работы: изучение средств и методов измерения параметров электрических цепей; оценка результатов и погрешностей измерений.
Основные теоретические положения
Результаты измерений нужно представить в виде
|
(1) |
где
 – сопротивление измеряемого резистора,
определяемое по шкале прибора; R
– абсолютная погрешность измерения
сопротивления.
– сопротивление измеряемого резистора,
определяемое по шкале прибора; R
– абсолютная погрешность измерения
сопротивления.
Рассмотрим
принцип оценки погрешностей для ряда
омметров, имеющих неравномерную шкалу
с диапазонами показаний 0∞,
∞0.
В таких приборах за нормирующее значение
LN
принимают геометрическую длину шкалы,
выраженную в делениях любой равномерной
шкалы, имеющейся у данного прибора. В
таких приборах класс точности имеет
особое обозначение, например,
 .
Численное значение класса точности при
таком его представлении означает
максимальную допустимую приведенную
погрешность омметра, в данном случае
определяемую как отношение максимально
допустимой абсолютной погрешности
прибора, выраженной в делениях, к длине
LN
шкалы омметра в тех же делениях. Отсюда
следует двухступенчатая процедура
оценки погрешности результата измерений
сопротивления омметрами по его классу
точности. Сначала определяют предельную
абсолютную погрешность прибора,
выраженную в делениях любой равномерной
шкалы:
.
Численное значение класса точности при
таком его представлении означает
максимальную допустимую приведенную
погрешность омметра, в данном случае
определяемую как отношение максимально
допустимой абсолютной погрешности
прибора, выраженной в делениях, к длине
LN
шкалы омметра в тех же делениях. Отсюда
следует двухступенчатая процедура
оценки погрешности результата измерений
сопротивления омметрами по его классу
точности. Сначала определяют предельную
абсолютную погрешность прибора,
выраженную в делениях любой равномерной
шкалы:
|
(2) |
где
LN
– нормирующее значение равномерной
шкалы, выраженное в делениях шкалы; k
– класс точности прибора. Для того чтобы
определить погрешность в единицах
измерения сопротивления, необходимо
подключить магазин сопротивлений к
вольтметру и установить полученное
значение сопротивления резистора на
магазине сопротивлений. Далее с помощью
магазина сопротивлений, изменяя значения
сопротивления магазина, отложить по
равномерной шкале вправо, а затем влево
предельную абсолютную погрешность ∆L,
рассчитанную по (2), фиксируя при этом
получаемые значения магазина сопротивлений.
Определив разность между показаниями
магазина сопротивлений и номинальным
значением, полученным с помощью
вольтметра, результат измерения следует
записать в виде
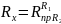 .
.
Спецификация средств измерений, применяемых при эксперименте
Наименование средства измерений |
Диапазоны измерений, постоянные СИ |
Характеристики точности СИ, классы точности |
Рабочий диапазон частот |
Параметры входа (выхода) |
Вольтметр универсальный В7-26 |
10 Ом – 1000 МОм |
|
- |
|
Вольтметр универсальный цифровой GDM–8135 |
200 Ом – 2000 кОм
20 МОм |
1 ед. мл. разряда
1 ед. мл. разряда |
- |
|
Измеритель иммитанса Е7–21 |
Режим омметра |
|||
1 мОм – 20 МОм |
- |
100 Гц – 1 кГц |
- |
|
Режим измерения ёмкости |
||||
0,1 пФ – 20 мФ |
- |
1 кГц |
- |
|
Режим измерения
|
||||
по |
- |
1 кГц |
- |
|
Режим измерения индуктивности |
||||
0,1 мкГн – 16 кГн |
- |
1 кГц |
- |
|
Режим измерения |
||||
по |
- |
1 кГц |
- |
|
Режим измерения добротности |
||||
|
- |
1 кГц |
- |
|
Обработка результатов
1. Измерение сопротивления резисторов
1.1. Измеритель импеданса
Расчёт погрешности:
Для

 ,
где
,
где
 – конечное значение установленного
диапазона измерений; R
– измеренное значение сопротивления.
– конечное значение установленного
диапазона измерений; R
– измеренное значение сопротивления.
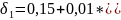 %
%

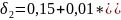 %
%
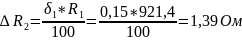
Для

 ,
где
,
где
 – начальное значение установленного
диапазона измерений; R
– измеренное значение сопротивления
– начальное значение установленного
диапазона измерений; R
– измеренное значение сопротивления
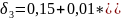 %
%

Результаты измерений:



1.2. Универсальный электронный вольтметр
Абсолютная
погрешность
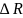 результата измерений оценивается по
приближённой формуле
результата измерений оценивается по
приближённой формуле
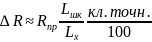 ,
где
– показания прибора;
,
где
– показания прибора;
 – длина
любой равномерной шкалы данного прибора,
выраженная в делениях шкалы;
– длина
любой равномерной шкалы данного прибора,
выраженная в делениях шкалы;
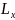 – длина участка этой же шкалы от нулевой
отметки до положения указателя при
изменении сопротивления, выраженная в
тех же делениях шкалы; кл.точн. – класс
точности прибора в режиме омметра.
– длина участка этой же шкалы от нулевой
отметки до положения указателя при
изменении сопротивления, выраженная в
тех же делениях шкалы; кл.точн. – класс
точности прибора в режиме омметра.
и
класс точности – величины постоянные
для всех трёх измерений, поэтому примем
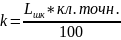 и вычислим этот коэффициент:
и вычислим этот коэффициент:
 .
.
Теперь
 .
.



Результаты измерений:

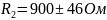

1.3. Универсальный цифровой вольтметр
Расчёт погрешности:
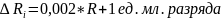



Результаты измерений:

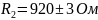

2. Измерение ёмкости и тангенса угла потерь конденсатора
2.1. Последовательная схема замещения
Расчёт погрешности:
 ,
где
,
где
 – начальное значение установленного
диапазона измерений; C
– измеренное значение ёмкости.
– начальное значение установленного
диапазона измерений; C
– измеренное значение ёмкости.

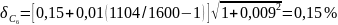





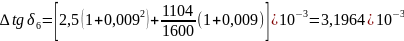
Результаты измерений:


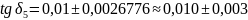

2.2. Параллельная схема замещения
Т.к.
значения
 ,
,
 ,
,
 ,
,
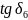 при последовательной и параллельной
схемах замещения совпадают, а расчёты
погрешностей проводятся по тем же
формулам, то результаты измерений будут
совпадать с итогом п.2.1.
при последовательной и параллельной
схемах замещения совпадают, а расчёты
погрешностей проводятся по тем же
формулам, то результаты измерений будут
совпадать с итогом п.2.1.
3. Измерение индуктивности и добротности катушки
3.1. Последовательная схема замещения
Расчёт погрешности:
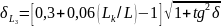
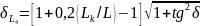 ,
где
,
где
 – конечное значение установленного
диапазона измерений; L
– измеренное значение индуктивности.
– конечное значение установленного
диапазона измерений; L
– измеренное значение индуктивности.



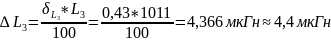





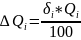


Результаты измерений:


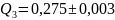

3.2. Параллельная схема замещения
Расчёт погрешности:
 ,
где
– конечное значение установленного
диапазона измерений; L
– измеренное значение индуктивности.
,
где
– конечное значение установленного
диапазона измерений; L
– измеренное значение индуктивности.


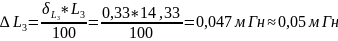

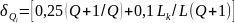



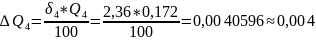
Результаты измерений:
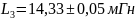
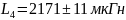
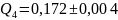
Вывод: в результате проведения лабораторной работы было установлено, что измерение сопротивления измерителем импеданса является наиболее точным, в то время как измерение при помощи универсального электронного вольтметра дало самый неточный результат. При измерении ёмкости и тангенса угла потерь конденсатора было обнаружено, что измеряемые значения не меняются при переключении с последовательной схемы замещения на параллельную. В случае индуктивности, её значение менялось при смене схемы, в отличие от значения добротности.


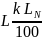
 от длины шкалы
от длины шкалы
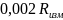 +
+
 +
+