
- •ВВЕДЕНИЕ
- •1. ВЫПОЛНЕНИЕ ЭСКИЗОВ ДЕТАЛЕЙ МАШИН
- •1.1. Общие сведения
- •1.2. Последовательность выполнения эскиза
- •2.3. Расчет и эскизирование конических зубчатых колес
- •3.2. Выполнение эскиза детали типа «вал» с натуры
- •4. СТАНДАРТИЗИРОВАННЫЕ ЭЛЕМЕНТЫ
- •4.1. Нормальные линейные и угловые размеры
- •4.2. Резьбы
- •4.3. Радиусы закруглений и фаски
- •4.4. Центровые отверстия
- •4.5. Рифления прямые и сетчатые
- •4.6. Шпоночные соединения
- •4.8. Канавки для выхода шлифовального круга
- •4.9. Штифтовые соединения
- •4.10. Лыски, квадраты, шестигранники
- •4.11. Сальниковые уплотнительные кольца
- •4.12. Материалы, применяемые для изготовления деталей
- •5. ОБОЗНАЧЕНИЕ ШЕРОХОВАТОСТИ ПОВЕРХНОСТЕЙ
- •5.1. Параметры шероховатости поверхностей
- •5.2. Правила обозначения шероховатости поверхностей
- •5.3. Правила нанесения обозначений шероховатости на чертеже
- •ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
- •ЗАКЛЮЧЕНИЕ
- •БИБЛИОГРАФИЧЕСКИЙ СПИСОК
- •ОГЛАВЛЕНИЕ

По этому приближенному значению модуля m(пр) выбирают действительное значение модуля m, как ближайшее к расчетному значение из таблицы по ГОСТ 9563–60 (табл. 1).
По выбранному из таблицы значению модуля определяют диаметр делительной окружности d, диаметр окружности вершин da и диаметр окружности впадин df по формулам.
Все остальные размеры, необходимые для вычерчивания эскиза зубчатого колеса, находят измерением элементов колеса.
2.3. Расчет и эскизирование конических зубчатых колес
Коническая передача отличается от цилиндрической тем, что катки, перекатывающиеся один по другому без скольжения, представляют собой два конуса (рис. 26).
Рис. 26. Коническая зубчатая передача
Зубья на боковых поверхностях конусов также отличаются от зубьев цилиндрических колёс. Их размеры (высота, ширина и др.) постепенно уменьшаются по мере приближения к вершине конуса. Поэтому модуль и параметры контура зуба по длине имеют переменное
31

значение, т. е. на большей и меньшей начальн х окруж ностях конуса они различны
а |
|
б |
Рис. 27. Коническо |
зубчатое колесо с элемента |
и фиксации на валу |
при помощи |
поночного (а) и шлицевого |
б) соединений |
Конические колёса бывают с пр мыми, |
ангенциальным , кру- |
|
говым и, крив линейн ыми зубьями, а также с эвольвентной и циклоидальной линией зубьев. На валу колеса фиксируются, например, при помо щи шпоночного ( ис. 27, а) или шлицевого (рис. 27, б) соединений.
2.3.1. Расчет кон ических зубчатых колес
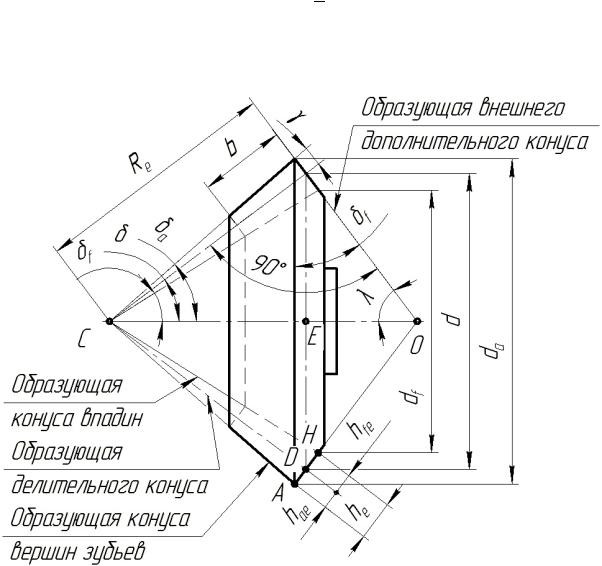
Форму и размер ы зуба к нического колеса (рис. 27) определяют следующие коническ е поверхности (рис. 28): делительный конус, конус вершин зубьев, конус впадин, а также ополни ельный внешний конус, образующие которого перп ендикулярны образующим делительного конуса.
При выполнении чертежей и эскизов (см . рис. 31) принимают, что делитель ный конус, а также конусы вершин зу ьев и впадин имеют общую вершину, как показано на рис. 28 .
Сечение зубчатого колеса внешним дополнительным конусом называется торцовым сечением. Делительная окружность – это окружность, по которой делительный конус пересекается с вн шним дополнительным кон сом, она расположена на торцовом сечении. Делительная кружность характеризуется делительным диаметром d, и ей соответствует внешний окружной делительный модуль те.
32
Значения модуля те определяются так же, как и для цилиндрического прямозубого колеса, и равно отношению диаметра делительной окружности к числу зубьев:
mе = .
Высота головки haе и ножки hfе зуба конического колеса измеряется по образующей внешнего дополнительного конуса.
Рис. 28. Параметры конического зубчатого колеса
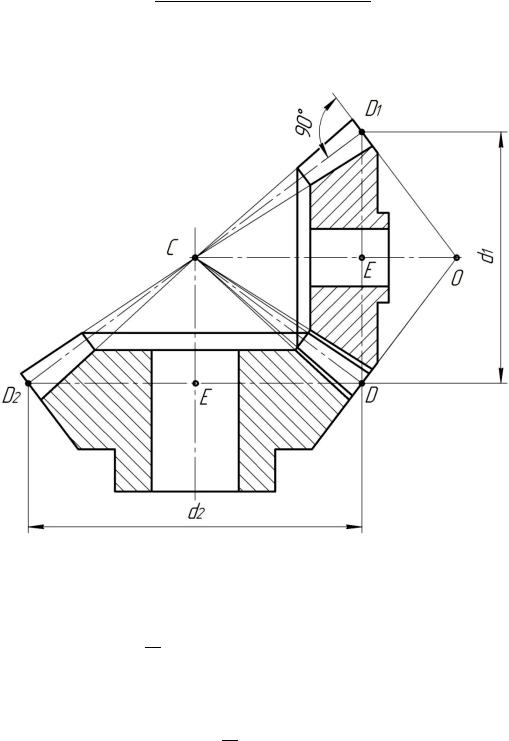
Приведем соотношения, позволяющие определить параметры зубчатого венца шестерни – зубатого колеса с меньшим числом зубьев (см. рис. 27) ортогональной конической передачи, основными параметрами которой являются внешний окружной делительный модуль передачи те, число зубьев шестерни z1, число зубьев колеса (зубчатое колесопередачисбольшимчисломзубьев) z2. Онипоказанынарис. 29:
– делительный диаметр шестерни (отрезок DD1) d1 = mez1;
– делительный диаметр колеса (отрезок DD2) d2 = mez2;
33
– высота головки зуба (отрезок AD) |
ha = те; |
|
||||||||||||
– высота ножки зуба (отрезок HD) |
hf = l,2me; |
|
||||||||||||
– высота зуба (отрезок АН) h = ha + hf = те + l,2me = 2,2me; |
|
|||||||||||||
– окружной шаг зубьев |
pt = meπ; |
|
|
|
|
|||||||||
– длина образующей делительного конуса шестерни Re (отрезок |
||||||||||||||
DC) определяется по формуле |
|
|
|
|
, |
|||||||||
Re= |
√ |
|
|
|
|
|
|
0,5 |
0,5 |
|
0,5 |
|
||
|
|
e |
|
|
|
|
|
|
|
|||||
иначе R |
|
= |
|
|
= |
|
; |
|
|
|
|
|||
Рис. 29. Изображение конической зубчатой передачи
– угол делительного конуса δ (угол наклона образующей начального конуса к его оси) определяют по формулам:
шестерни tg δ1 = ,
так как отрезок DE = 0,5DD1 = 0,5d1 = 0,5mez1,
а отрезок СЕ = 0,5d2 = 0,5mez2, то tg δ1 = ;
аналогично колеса tg δ2 = ;
34

– угол внешнего дополнительного конуса определяют по фор-
муле = 90° – δ;
– угол головки зуба tg = |
|
|
= |
|
; |
|
||
|
|
|
||||||
– угол ножки зуба tg f = |
|
|
= |
, |
|
; |
||
|
|
|||||||
–угол конуса вершин δa = δ + ;
–угол конуса впадин δf = δ – f .
Рабочие чертежи и эскизы конических зубчатых колёс выполняют в соответствии с требованиями ГОСТ 2.405–75. На изображении конического зубчатого колеса указывают:
–диаметр большего основания конуса вершин и при необходимости предельное значение радиального биения поверхности вершин;
–расстояние от большего основания конуса вершин до опорной торцовой плоскости;
–угол конуса вершин и при необходимости предельное значе-
ние радиального биения поверхности конуса вершин у большего
именьшего оснований;
–угол внешнего дополнительного конуса;
–ширину зубчатого венца (по образующей делительного конуса), за исключением случаев, когда передний торец зубчатого колеса выполняют плоскосрезанным;
–длину образующей делительного конуса и при необходимости (для колёс с круговыми зубьями) длину средней образующей делительного конуса;
–расстояние от вершины делительного конуса до опорной торцовой плоскости;
–шероховатость рабочих боковых поверхностей зубьев (по делительной окружности), поверхности конуса вершин и поверхности впадин;
–рабочий профиль зубьев зубчатых колёс (при необходимости);
–размеры фасок или радиусы закруглений на кромках зубьев, образованных конусом вершин и дополнительным конусом, а также на кромках головок и торцов зубьев.
2.3.2. Выполнение эскиза прямозубого конического колеса с натуры
Для того чтобы выполнить с натуры эскиз или чертеж конического прямозубого колеса ортогональной передачи, необходимо оп-
35
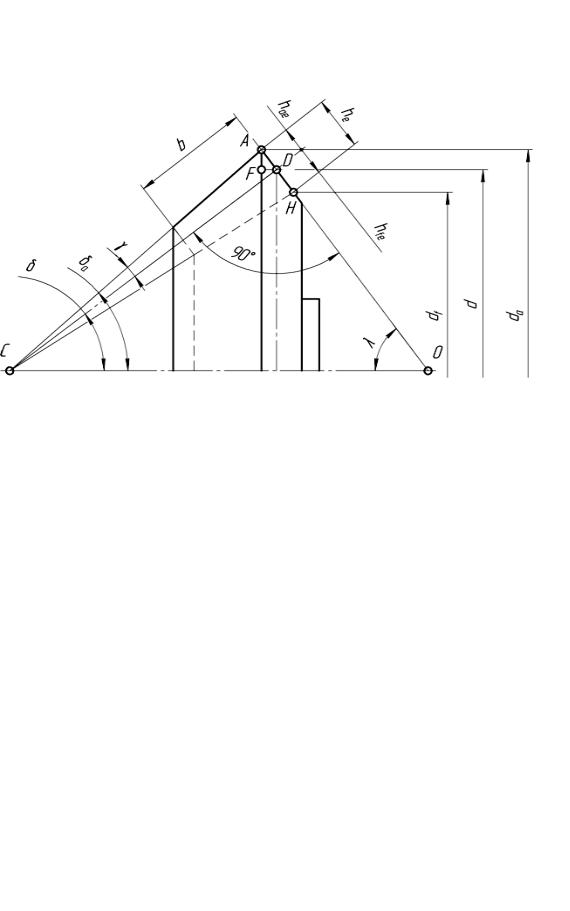
ределить его одуль т е. В первую оче едь при помощи угломе а следует змерить угол внешнего дополнительного конуса λ (рис. 28, 30), тогда λ = 90 – δ, где δ = δа – γ. 
Рис. 30. Определение параметров конического зуб чатого колеса с нат ры
Затем подсчитывают уго л делительного конуса δ: |
|
|
δ = 90° – λ. |
|
|
Измерив диаметр окружности вершин зубьев da |
и подсчитав |
|
число зубьев z , определяют модуль те. |
|
|
Для определения те ра смотри |
прямоугольный |
треугольник |
AFD на рис. 30. Гипотенуза A D равна |
высоте головки |
зуба ha = те. |
Катет AF равен половине разности диаметра окружности вер ин da зубьев и дели ельной окружности d: 
F = |
|
. |
|
|
|
|
|
||
Угол DA F равен углу δ (углы с соответс венно перпендикуляр- |
||||
ными сторонами), поэтому AF = AD cosδ = теcosδ = |
|
. |
||
|
||||
Так как делительный диаметр d = mez, то можно написать:
Отсюда |
теc osδ = |
|
|
. |
|
|
|
||||
|
е = |
|
|
. |
|
|
|
δ |
|||
Поскольку при выполнении приведенных выше расчетов произ-
водились замеры некоторых элементо , то подсчитанное значение те будет прибли женным mе(пр). 
36
37
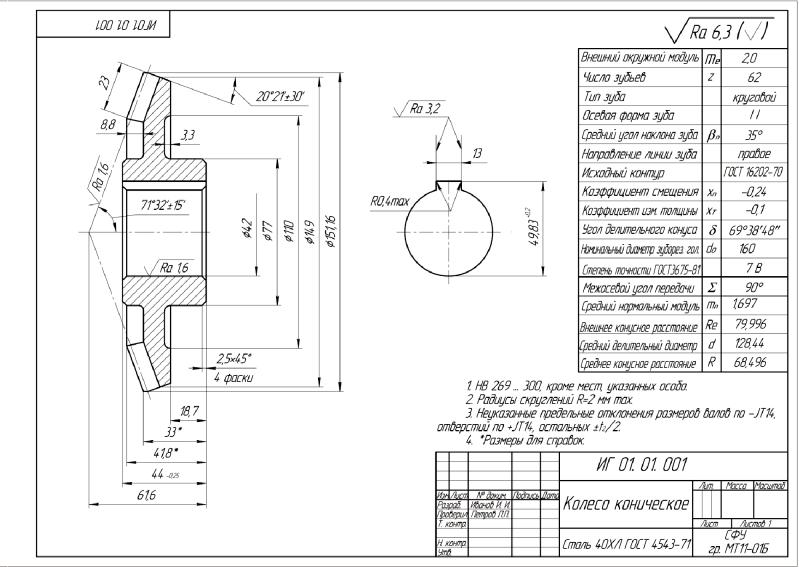
Рис. 31. Эскиз конического зубчатого колеса с прямыми зубьями
По полученному приближенному значению модуля mе(пр) выбирают действительное значение модуля mе как ближайшее к расчетному значение из таблицы по ГОСТ 9563–60 (табл. 1).
По выбранному из таблицы значению модуля рассчитывают диаметр делительной окружности d по формуле d = mez. Затем замеряют ширину венца b, как показано на рис. 28, 30, и остальные конструктивные элементы зубчатого колеса. После чего приступают к вычерчиванию эскиза или чертежа.
На рис. 31 приведен пример выполнения эскиза конического зубчатого колеса с прямыми зубьями. В правом верхнем углу чертежа помещают таблицу параметров зубчатого колеса (см. рис. 22).
38

3.ВЫПОЛНЕНИЕ ЭСКИЗА
ДЕТАЛИ ТИПА «ВАЛ»
3.1 . Конс рукти ные и технологичес ие эле менты вала
Вал – эт о подвижная деталь машины (стержень), вращающаяся в опорах (подшипниках) для передачи вращательного движения и крутящего момента с помощью зубчатых колес, шкивов и т. п.
Рис. 32. Конст руктивны и технологически элемент ы вала
Независимо от сложности, вал изображается как совокупность простейших геометри еских т л или частей.
39
