
- •Принципы построения потоковых шифров
- ••Шифр гаммирования – поточный, т.е. шифруются последовательно биты или символы открытого сообщения m.
- ••Функция расшифрования для криптопреобразования гаммирования:
- ••Перед началом работы в шифраторы гаммирования на приёме и передаче вводятся одинаковые ключевые
- •.Принцип потокового шифрования
- •Требования к шифрующей гамме
- •Структурная схема формирователя гаммы
- •Линейный рекуррентный регистр
- •Пример ЛРР
- •Свойства ЛРР
- ••Максимальность периода
- •Примитивные многочлены
- •Пример вычисления периода ЛРР
- •Алгебраические свойства ЛРР
- •3. Свойство быстрого нахождения любого
- •Свойство предсказуемости
- •Статистические свойства примитивных ЛРР
- ••3. Свойства окна. Если вдоль ЛРП перемещается "окно" шириной n символов, то в
- •5. Автокорреляционная функция выходной последовательности ЛРР
- •Назначение нелинейных узлов
- •Типовые нелинейные узлы
- •Определение Пусть задана двоичная последовательность b
- •Пояснение линейной эквивалентной
- •Пример увеличения линейной сложности последовательности с помощью нелинейных устройств
- •Расчет ЛЭС для узла перемножения
- •Другие способы построения ФШГ
- •Формирователь ШГ на нескольких ЛРР
- •Пример. Рассмотрим случай, когда имеется три ЛРР с длинами n1,n2 ,n3 , а
- •Формирователь ШГ на основе ЛРР с управляемым тактированием
- •Доказывается [9 ], что период T выходной последовательности y
- •Основные требования, предъявляемые к разработке стойкого
- •Структурная схема формирователя шифрующей гаммы по алгоритму А5
- •Анализ стойкости алгоритма A5/1
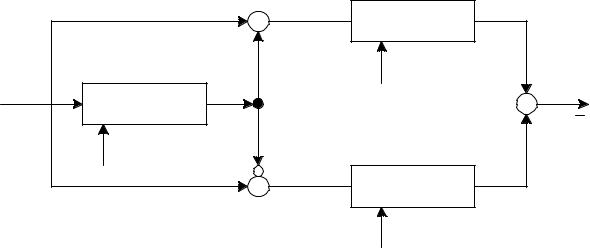
- •Структурная схема формирователя шифрующей гаммы по алгоритму А5/2
- •Преимущества потоковых шифров
- •Поточный шифр RC4
- •Алгоритм формирования гаммы
Назначение нелинейных узлов
Определение: Функция y=f(x1x2…xm) называется линейной, если она может быть представлена в виде суммы аргументов по модулю два, в противном случае функция нелинейная.
y= a1x1+ a2x2+….+ amxm, |
ai 0,1 |
Пример нелинейной функции y=1+x5+x1x2+x2x3x4
К
 ЛРР К
ЛРР К 


НУУ
ШГ
21

Типовые нелинейные узлы
X1 |
|
|
|
X1 |
1 |
|
|
& |
|
|
|
Y=X1vX2 |
|||
Y Y=X1&X2 |
|
Y |
|||||
|
|
|
|||||
|
|
|
|
||||
X2 |
|
|
|
X2 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X1 |
Дж |
|
Если Х3=1, то |
||
|
|
|
|
Y |
|
X2 |
|
||||
|
|
|
|
|
Y=Х1, |
X3 |
|
|
|||
|
|
|
|
|
если Х3=0, то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y=Х2 |
X1 |
|
|
Если Х3=1, то |
||
Ул |
|
||||
|
Y= X1&X2, |
||||
|
|
|
|
Y |
|
X2 |
|
||||
|
|
если Х3=0, то |
|||
|
|
||||
|
|
|
|
|
|
X3 |
|
|
|||
|
|
Y= X1vX2 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
n |
Дж |
Дж |
Дж |
УЛ
ШГ
Дж –элемент Джеффа |
|
УЛ – элемент управляемая логика |
22 |

Определение Пусть задана двоичная последовательность b
длины N . Тогда линейной эквивалентной сложностью
(ЛЭС) этой последовательности называется минимальная длина такого ЛРР, который, при некотором начальном заполнении и некотором выборе обратных связей, может сгенерировать в точности ту же самую последовательность b .
Очевидно, что всегда выполняются неравенства: 0 L b N
23

Пояснение линейной эквивалентной
• . |
сложности |
|
L>>n
ЛРР (n)
|
|
ШГ |
|
|
ЛРР (L) |
||
|
|||
|
|
||
|
|
|
НУУ
ШГ
24

Пример увеличения линейной сложности последовательности с помощью нелинейных устройств
h(x)=x4+x+1
b0=1, b1=0, b2=0, b3=0
|
h(x)=x10+x5+1 |
y=bi1bi2bi4 |
b7=1, b9=b8=b6=b5=b4=b3=b2=b1=b0=0 |
25

Расчет ЛЭС для узла перемножения |
L y n n 1 |
|
2 |
Расчет ЛЭС последовательности, полученной перемножением m выходов ЛРР
|
|
|
|
ЛРР |
|
|
|
|
|
2 |
|
|
m 1 |
m |
1 |
|
|
|
||
L( y) Cnk |
|
|
|
|
|
|
k 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
где Ckn n!/ k!(n k)! -число сочетаний из n элементов по k
Если все расстояния между отводами одинаковы, т.е. 1 2 m 1 и выполняется дополнительное условие gcd(2n 1, ) 1, то линейная эквивалентная сложность имеет также следующую нижнюю границу [ 9]:
L(y) Cnm |
(3.65) |
|
26 |

Другие способы построения ФШГ
• 1. Применение нескольких ЛРР
ЛРР1 (n1) |
|
|
Элемент |
|
|
|
|
||
|
|
|
Джеффе |
|
|
|
|||
|
|
|
|
|
ЛРР2 (n2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЛРР3 (n3) |
|
|
|
|
|
|
|
|
|
2. Применение нерегулярного тактирования
ЛРР1
ГТЧ
ЛРР2
27

Формирователь ШГ на нескольких ЛРР
Пусть в нашем распоряжении имеется m ЛРР. Тогда можно рассмотреть
метод формирования гаммы, показанный на Рис.3.27, где f x1, x2 , , xm – произвольная булева функция, а n1,n2 ,...nm - длины соответствующих ЛРР.
|
|
|
x1 |
|
|
|
|
ЛРР1(n |
1 |
) |
|
|
|||
x2 |
|
y |
|||||
|
|
|
|
||||
ЛРР2(n |
2 ) |
f (x1, x2, , xm ) |
|||||
|
|
|
|||||
|
|
|
|||||
|
|
|
xm |
|
|
||
|
|
|
|
|
|||
ЛРРm(n |
m |
) |
|
|
|||
|
|
|
|
||||
Утверждение 3.4 [9 ]. Если длины ЛРР n1 , n2 ,...nm все различны и больше 2, а
булева функция f (x1...xm ) представлена в алгебраически нормальной форме (АНФ) (смотри раздел 3.1.8), то ЛЭС может быть вычислена после подстановки в АНФ длин соответствующих ЛРР, то есть:
L( y) f (n1 , n2 ,..., nm ) |
(3.66) |
(Заметим, что вычисления в (3.66) должны производиться как в обычной28 арифметике, а не в поле GF(2).)
Пример. Рассмотрим случай, когда имеется три ЛРР с длинами n1,n2 ,n3 , а в качестве булевой функции используется генератор Джеффа.
Представим булеву функцию, описывающую этот генератор (смотри Рис.3.27), в АНФ: y x1 x2 x2 x3 x3 (x2 – управляющий вход).
Используя (3.66), получаем:
L(y) n1n2 n2 n3 n3 |
(3.67) |
В [9] доказано, что если длины ЛРР n1,n2 ,n3 , входящих в генератор Джеффа, являются взаимно простыми числами, то период его выходной
последовательности будет равен (2n1 1)(2n2 1)(2n3 1) .
29
Формирователь ШГ на основе ЛРР с управляемым тактированием
|
|
|
ТИ 1 |
|
|
|
|
ЛРР-1(n |
2 |
) |
|
ТИ |
|
|
k2 |
|
|
|
ЛРР-1(n 1 ) |
|
|
y |
|
|
|
|
|
|
|
|
|
k1 |
ТИ 2 |
|
|
|
|
|
|
|
|
|
|
ЛРР-1(n |
3 |
) |
k3
В этой схеме ЛРР-1 тактируется регулярно импульсами ТИ, а ЛРР-2 и ЛРР-3 тактируются нерегулярно, в зависимости от наличия или отсутствия импульсов ТИ-1, ТИ-2 соответственно, вырабатываемых псевдослучайно при помощи выходной последовательности ЛРР-1. Ключи k1, k2 , k3 вводятся как
начальные состояния ЛРР-1,2,3, имеющих длины n1,n2 , n3 , соответственно. Если выход ЛРР-1 равен 1, то ЛРР-2 продвигается, а ЛРР-3 не продвигается, и на его выходе повторяется предыдущий символ. Если выход ЛРР-1 равен 0, то ЛРР-3 продвигается, а ЛРР-2 не продвигается, и на его выходе повторяется
предыдущий символ. |
30 |
