Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Балтийский федеральный университет им. И.Канта

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Internet.Security

.pdf

Скачиваний:

Добавлен:

10.02.2015

Размер:

3.75 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 1213 / 4313 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

100 INTERNET SECURITY

Round	A			B			C	D

11	ce5ac268			4a1d83c3			42aa5994	31cdfe66
12	4a1d83c3			113537e5			31cdfe66	5db94923
13	113537e5			4b1b6674			5db94923	e3632504
14	4b1b6674			f60dd47f			e3632504	0750ccfe
15	f60dd47f			95a4e7a0			0750ccfe	b1e27064
16	95a4e7a0			442babe9			b1e27064	f229c1dc
17	442babe9			cb3a05f9			f229c1dc	fadd06ef
18	cb3a05f9			4ce5dc7b			fadd06ef	a76a5ba6
19	4ce5dc7b			3e3439e9			a76a5ba6	f105f04e
20	3e3439e9			23c61547			f105f04e	183fa47e

Final value in each register:				F
A = 2f194e52	B = 23c61547			F
A = 2f194e52	B = 23c61547			M	Y
C = 36f6511f	D = 183fa47e			M
C = 36f6511f	D = 183fa47e			L
			A
Thus, the ciphertext is computed as:
52 4e	19 2f	E				f6	36 7e a4 3f	18
52 4e	19 2f	47	15	c6 23 1f 51		f6	36 7e a4 3f	18

3.4.4 DecryptionT

RC6 decryption works with four w-bit registers A, B, C, D which contain the initial output ciphertext at the end of encryption. The ﬁrst byte of ciphertext is placed into the least signiﬁcant byte of A. The last byte of ciphertext is placed into the most signiﬁcant byte of D.

The RC6 decryption algorithm is illustrated as shown below: Decryption with RC6-w/r/b

Input: Ciphertext stored in four w-bit input registers A, B, C, D Number of rounds, r

w-bit round keys S[0, 1, . . . , 2r + 3] Output: Plaintext stored in A, B, C, D

Procedure:C = C − S[2r + 3]

A = A − S[2r + 2] for i = r down to 1 do

{

(A, B, C, D) = (D, A, B, C)

u = (D × (2D + 1)) <<< 1g w t = (B × (2B + 1)) <<< 1g w C = ((C − S[2i + 1] >>> t) u

Team-Fly®

SYMMETRIC BLOCK CIPHERS

101

A = ((A − S[2i]) >>> u) t

}

D = D − S[1]

B = B − S[0]

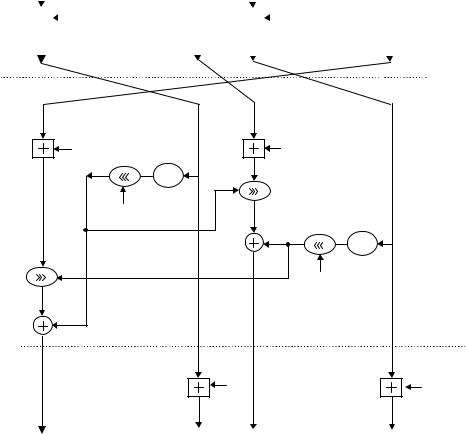
The decryption of RC6 is depicted as shown in Figure 3.13.

Example 3.18 Consider again RC6-32/20/16. Utilising Figure 3.13 for RC6 decryption, the input is the ciphertext stored in four 32-bit input registers A, B, C and D.

−S[2i + 3]

−S[2i + 2]

−S[2i]		−S[2i + 1]
f
			Repeat for
lg w			i rounds
lg w		u
t		u
t
			f
		lg w
		−S[0]	−S[1]
A	B	C	D
Figure 3.13	RC6-w/r/b decryption scheme.

102		INTERNET SECURITY
Initial value in each register:
A = 3e3439e9	B = 23c61547
C = f105f04e	D = 183fa47e
Decryption process

Round	A	B	C	D

1	4ce5dc7b	3e3439e9	a76a5ba6	f105f04e
2	cb3a05f9	4ce5dc7b	fadd06ef	a76a5ba6
3	442babe9	cb3a05f9	f229c1dc	fadd06ef
4	95a4e7a0	442babe9	b1e27064	f229c1dc
5	f60dd47f	95a4e7a0	0750ccfe	b1e27064
6	4b1b6674	f60dd47f	e3632504	0750ccfe
7	113537e5	4b1b6674	5db94923	e3632504
8	4a1d83c3	113537e5	31cdfe66	5db94923
9	ce5ac268	4a1d83c3	42aa5994	31cdfe66
10	8fde9634	ce5ac268	84ceecec	42aa5994
11	662fc8cb	8fde9634	7e9553f1	84ceecec
12	49dd0a20	662fc8cb	0035d1db	7e9553f1
13	f8754ace	49dd0a20	8cc61508	0035d1db
14	8c83dd52	f8754ace	ef7cbe5d	8cc61508
15	5013ef46	8c83dd52	53caa736	ef7cbe5d
16	9300620e	5013ef46	2d144999	53caa736
17	fd35085f	9300620e	8d81f7b9	2d144999
18	a17a48d4	fd35085f	fdbc336a	8d81f7b9
19	7eaff47e	a17a48d4	d684c550	fdbc336a
20	35241302	7eaff47e	bdac9b8a	d684c550

Final value in each register
A = 35241302	B = 79685746
C = bdac9b8a	D = f1e0dfce

Thus, the recovered plaintext is computed as:

02 13 24 35 46 57 68 79 8a 9b ac bd ce df e0 f1

Example 3.19 Consider RC6-32/20/16. Assume that the plaintext and user key are given as follows.

Plaintext: b267af31	6d8259e7	b16ac385 f2a072be
User key: de 37	a1 fd 84	92 d8 ef e7 14 f1 b7 cc 78 3a ad

			SYMMETRIC BLOCK CIPHERS				103
Converting the secret key from bytes to words:
L[0] = f2baabd4			L[1] = 73e727d4
L[2] = edc4db16			L[3] = 45c0de8b
Mixing in the secret key S:

S[0] = 62e429de			S[1] = 3bdc27f1		S[2] = daf4e1c8		S[3] = 16c26209
S[4] = b22edecc			S[5] = 509c1331		S[6] = 3487c3db		S[7] = 2b8adb1e
S[8] = 5e4c1907			S[9] = 14458ba5		S[10] = 18da3591		S[11] = 8fcdd4b5
S[12] = 5a76c846			S[13] = 2085c465		S[14] = 78c44f1a		S[15] = 344b8269
S[16] = cd810b25			S[17] = a4c787e8		S[18] = 4fcc683d		S[19] = f0d0d987
S[20] = 1d1a587a			S[21] = b55757dc		S[22] = c3d68827		S[23] = bfcc8533
S[24] = 094a038c			S[25] = 5c4b0c8e		S[26] = 4aa837e7		S[27] = ae2430af
S[28] = 2e5e3577			S[29] = 305afc61		S[30] = 3e3b932a		S[31] = 3db9bd11
S[32] = 9a891917			S[33] = 1982ee95		S[34] = eabbfb7a		S[35] = 4da6c90
S[36] = 0b0945ad			S[37] = 16059bf7		S[38] = a4fcfe21		S[39] = aa2c586f
S[40] = 3e05d045			S[41] = 5fbe7c05		S[42] = 974646ea		S[43] = d4af0053
Encryption:
Compute the ciphertext of RC6-32/20/16.
Initial values in registers:
A = b267af31	B = 6d8a59e7
C = b16ac385	D = f2a072be
Encryption process

Round			A	B		C	D

1		d06e83c5		0fbe58ad		2e7c9aaf	82122047
2		0fbe58ad		aebf8fe0		82122047	4c5209fc
3		aebf8fe0		1eea2af6		4c5209fc	671ab020
4		1eea2af6		4c0793b9		671ab020	7dcf4468
5		4c0793b9		d02f880f		7dcf4468	e1f57f20
6		d02f880f		76e50556		e1f57f20	040efeb0
7		76e50556		9226cc1b		040efeb0	6bc6f374
8		9226cc1b		06a119a3		6bc6f374	97683738
9		06a119a3		85830598		97683738	250fbfe5
10		85830598		1c28dc0a		250fbfe5	c89c019f
11		1c28dc0a		adb7d6c6		c89c019f	c28f0f4b
12		adb7d6c6		1911f356		c28f0f4b	d547cb27
13		1911f356		8a0b16e8		d547cb27	2c1d3ae4
14		8a0b16e8		08ddf156		2c1d3ae4	bed49d1e

104 INTERNET SECURITY

Round	A	B	C	D

15	08ddf156	c77d14d5	bed49d1e	4fc7085f
16	c77d14d5	474b1fd6	4fc7085f	67ffbcff
17	474b1fd6	327894f2	67ffbcff	99d3105c
18	327894f2	438277f7	99d3105c	7351c0e7
19	438277f7	ff8422c8	7351c0e7	3e0b9530
20	ff8422c8	ce15ebd7	3e0b9530	f3ca4bd4

Final value in each register:
A = 96ca69b2	B = ce15ebd7
C = 12ba9583	D = f3ca4bd4

Thus, the ciphertext is computed as: A||B||C||D =

96ca69b2 ce15ebd7 12ba9583 f3ca4bd4

Decryption:

The initial values in registers A, B, C and D are output at round 19 at the end of encryption.

Decryption process

Round	A	B	C	D

1	438277f7	ff8422c8	7351c0e7	3e0b9530
2	327894f2	438277f7	99d3105c	7351c0e7
3	474b1fd6	327894f2	67ffbcff	99d3105c
4	c77d14d5	474b1fd6	4fc7085f	67ffbcff
5	08ddf156	c77d14d5	bed49d1e	4fc7085f
6	8a0b16e8	08ddf156	2c1d3ae4	bed49d1e
7	1911f356	8a0b16e8	d547cb27	2c1d3ae4
8	adb7d6c6	1911f356	c28f0f4b	d547cb27
9	1c28dc0a	adb7d6c6	c89c019f	c28f0f4b
10	85830598	1c28dc0a	250fbfe5	c89c019f
11	06a119a3	85830598	97683738	250fbfe5
12	9226c1b	06a119a3	6bc6f374	97683738
13	76e50556	9226cc1b	040efeb0	6bc6f374
14	d02f880f	76e50556	e1f57f20	040efeb0
15	4c0793b9	d02f880f	7dcf4468	e1f57f20
16	1eea2af6	4c0793b9	671ab020	7dcf4468
17	aebf8fe0	1eea2af6	4c5209fc	671ab020
18	0fbe58ad	aebf8fe0	82122047	4c5209fc
19	d06e83c5	0fbe58ad	2e7c9aaf	82122047
20	b267af31	d06e83c5	b16ac385	2e7c9aaf

SYMMETRIC BLOCK CIPHERS

105

The ﬁnal decrypted plaintext is:

b267af31 6d8a59e7 b16ac385 f2a072be

Example 3.20 Consider RC6-32/20/24. Suppose the plaintext and user key are given as follows:

Plaintext: 35241302			79685746		bdac9b8a		f1e0dfce
User key: 01	23	45	67	89	ab	cd	ef
01	12	23	34	45	56	67	78
89	9a	ab	bc	cd	de	ef	f0

The user supplies a key of b = 24 bytes, where 0 ≤ b ≤ 255. From this key, 2r + 4 = 44 words are derived and stored in the array S[0, 1, . . . , 2r + 3]. This array is used in both encryption and decryption.

Key array

S[0] = 4d80ade	S[1] = c85296a3	S[2] = c7ca853c	S[3] = d665bea0
S[4] = 4d34492f	S[5] = e110bf65	S[6] = 9f4acf83	S[7] = ed85cb10
S[8] = f9f0f8eb	S[9] = 2275ea3f	S[10] = e5dc8714	S[11] = a1b4b8b4
S[12] = 1a28cd0a	S[13] = 618fbe87	S[14] = 6fc1ede0	S[15] = 8eaf634d
S[16] = 7d213901	S[17] = bed7ab73	S[18] = 79ba092e	S[19] = 6179bc8a
S[20] = aa35b6f6	S[21] = 0091b3ca	S[22] = 65f970e9	S[23] = 687e9e94
S[24] = f17e5188	S[25] = 7ec55cf7	S[26] = fe2c8e93	S[27] = 2e7b3dae
S[28] = 56093cb8	S[29] = ed28fa03	S[30] = ab2eaaec	S[31] = d049366f
S[32] = fcd4cbd3	S[33] = 84b3906f	S[34] = 8eced9f1	S[35] = e02a2453
S[36] = 123b6e03	S[37] = a6192a81	S[38] = 8648252c	S[39] = b29fbd04
S[40] = 735d2dc1	S[41] = 97447b58	S[42] = 362b46b2	S[43] = 7c310342

RC6 works with four 32-bit registers A, B, C and D which contain the initial input plaintext as well as the output ciphertext at the end of encryption. Both encryption and decryption using RC6-32/20/24 are processed as shown below.

Initial values in registers:

A = 35241302	B = 79685746
C = bdac9b8a	D = f1e0dfce
Encryption with RC6-32/20/24

Round	A	B	C	D

0	35241302	7e406224	bdac9b8a	ba337671
1	7e406224	bf73145b	ba337671	ae7fec22
2	bf73145b	8223f9cc	ae7fec22	d96ddcb2
3	8223f9cc	823d1be2	d96ddcb2	8ad786e7
4	823d1be2	30fa9e1e	8ad786e7	3439983d

106 INTERNET SECURITY

Round	A	B	C	D

5	30fa9e1e	69de30e7	3439983d	41340557
6	69de30e7	1e5076a4	41340557	5cbef6d9
7	1e5076a4	a3202136	5cbef6d9	90578218
8	a3202136	48cd17be	90578218	36536a30
9	48cd17be	89b9dc8a	36536a30	6f54b847
10	89b9dc8a	e21b47ad	6f54b847	4927a4a1
11	e21b47ad	51ea2335	4927a4a1	21e33ea6
12	51ea2335	f6288913	21e33ea6	8dfa1819
13	f6288913	74cc2d40	8dfa1819	23c3a852
14	74cc2d40	3cfc9386	23c3a852	99050d00
15	3cfc9386	f0cd5501	99050d00	4f93af72
16	f0cd5501	f3d82818	4f93af72	096f38cb
17	f3d82818	1e600aa7	096f38cb	13e79bec
18	1e600aa7	f3af0e5c	13e79bec	38d4defa
19	f3af0e5c	99fe3cb6	38d4defa	aeb84edc
20	99fe3cb6	0405e519	aeb84edc	d49152f9

Thus, the output ciphertext at the end of encryption is:

d0298368 0405e519 2ae9521e d49152f9.

Decryption with RC6-32/20/24

Round	A	B	C	D

1	f3af0e5c	99fe3cb6	38d4defa	aeb84edc
2	1e600aa7	f3af0e5c	13e79bec	38d4defa
3	f3d82818	1e600aa7	096f38cb	13e79bec
4	f0cd5501	f3d82818	4f93af72	096f38cb
5	3cfc9386	f0cd5501	99050d00	4f93af72
6	74cc2d40	3cfc9386	23c3a852	99050d00
7	f6288913	74cc2d40	8dfa1819	23c3a852
8	51ea2335	f6288913	21e33ea6	8dfa1819
9	e21b47ad	51ea2335	4927a4a1	21e33ea6
10	89b9dc8a	e21b47ad	6f54b847	4927a4a1
11	48cd17be	89b9dc8a	36536a30	6f54b847
12	a3202136	48cd17be	90578218	36536a30
13	1e5076a4	a3202136	5cbef6d9	90578218
14	69de30e7	1e5076a4	41340557	5cbef6d9
15	30fa9e1e	69de30e7	3439983d	41340557
16	823d1be2	30fa9e1e	8ad786e7	3439983d
17	8223f9cc	823d1be2	d96ddcb2	8ad786e7
18	bf73145b	8223f9cc	ae7fec22	d96ddcb2
19	7e406224	bf73145b	ba337671	ae7fec22
20	35241302	7e406224	bdac9b8a	ba337671

SYMMETRIC BLOCK CIPHERS

107

Thus, the ﬁnal decrypted plaintext is:

35241302 79685746 bdac9b8a f1e0dfce.

3.5 AES (Rijndael) Algorithm

The Advanced Encryption Standard (AES) speciﬁed the Rijndael algorithm which is a FIFS-approved cryptographic algorithm developed by Daemen and Rijmen as an AES candidate algorithm in 1999. The Rijndael algorithm is a symmetric block cipher that can process data blocks of 128 bits using cryptographic keys of 128, 192 and 256 bits.

In this section, we will cover the algorithm speciﬁcation such as the key expansion routine, encryption by cipher and decryption by inverse cipher.

3.5.1Notational Conventions

•The cipher key for the Rijndael algorithm is a sequence of 128, 196 or 256 bits such that the index attached to a bit falls in between the range 0 ≤ i ≤ 128, 0 ≤ i ≤ 192 or 0 ≤ i ≤ 256, respectively.

•All byte values of the AES Rijndael algorithm are presented by a vector notation (b7, b6, b5, b4, b3, b2, b1, b0) which corresponds to a polynomial representation as:

b7x7 + b6x6 + b5x5 + b4x4 + b3x3 + b2x2 + b1x + b0 = bi xi

i=0

For example, (01001011) → x6 + x3 + x + 1.

•If there is an additional bit b8 to the left of an eight-bit byte, it will appear immediately to the left of the left bracket such as 1(00101110) = 1(2e).

•Arrays of bytes, a0, a1, a2, . . . , a15 are deﬁned from the 128-bit input sequence, ip0, ip1, ip2, . . . , ip126, ip127, as follows:

a0 = (ip0, ip1, . . . , ip7) a1 = (ip8, ip9, . . . , ip15)

a15 = (ip120, ip121, . . . , ip127)

where ipk denotes inputk for k = 0, 1, 2, . . . , 127.

In general, the pattern extended to longer sequence like 192and 256-bit keys is expressed as:

an = (ip8n, ip8n+1, . . . , ip8n+7), n ≤ 16.

108	INTERNET SECURITY

•The AES algorithm’s operations are internally performed on a two-dimensional array

of bytes called the state. The state consists of four rows of bytes. The state array Sr,c has a row number r, 0 ≤ r < 4, and a column number c, 0 ≤ c < N b, where Nb bytes are the block length divided by 32.

The input-byte array (in0, in1, . . . , in15) at the cipher is copied into the state array according to the following scheme:

Sr,c = in(r + 4c) for 0 ≤ r < 4 and 0 ≤ c < N b

and at the inverse cipher, the state is copied into the output array as follows: out (r + 4c) = Sr,c for 0 ≤ r < 4 and 0 ≤ c < N b.

An individual byte of the state is referred to as either Sr,c or S(r, c). The cipher and

inverse cipher operations are conducted on the state array as illustrated in Figure 3.14. For example, if r = 0 and c = 3, then in(0 + 12) = in(12) = S0,3; if r = 3 and

c = 2, then in(3 + 8) = in(11) = S3,2.

The four bytes in each column of the state form a 32-bit word, where the row number r provides an index for the four bytes within each word, and the column number c provides an index representing the column in this array.

3.5.2 Mathematical Operations

Finite ﬁeld elements (all bytes in the AES algorithm) can be added and multiplied. The basic mathematical operations will be introduced in the following.

Addition

The addition of two elements in a ﬁnite ﬁeld is achieved by XORing the coefﬁcients for the corresponding powers in the polynomials for two elements. For example,

(x5 + x3 + x2 + 1) + (x7 + x5 + x + 1) = x7 + x3 + x2 + x	(polynomial)
(00101101) (10100011) = (10001110)	(binary)
(2d) (a3) = (8e)	(hexadecimal)

Cipher input (bytes)

State array

Cipher output (bytes)

in0

in4

in8

in12

S0,0

S0,1

S0,2

S0,3

out0

out4

out8

out12

in1

in5

in9

in13

S1,0

S1,1

S1,2

S1,3

out1

out5

out9

out13

in2

in6

in10

in14

S2,0

S2,1

S2,2

S2,3

out2

out6

out10

out14

in3

in7

in11

in15

S3,0

S3,1

S3,2

S3,3

out3

out7

out11

out15

Figure 3.14 State array input and output.

SYMMETRIC BLOCK CIPHERS

109

Multiplication

The polynomial multiplication in GF(28) corresponds to the multiplication of polynomial modulo m(x) that an irreducible (or primitive) polynomial of degree 8 for the AES algorithm:

m(x) = x8 + x4 + x3 + x + 1

Example 3.21 Prove (73) • (a5) = (e3)

(01110011) • (10100101)

(x6 + x5 + x4 + x + 1) • (x7 + x5 + x2 + 1)

= x13 + x12 + x10 + x9 + x6 + x4 + x3 + x2 + x + 1

The modular reduction by m(x) results in

x13 + x12 + x10 + x9 + x6 + x4 + x3 + x2 + x + 1 mod (x8 + x4 + x3 + x + 1)

=x7 + x6 + x5 + x + 1

=(11100011) = (e3)

Since the multiplication is associative, it holds that

a(x)(b(x) + c(x)) = a(x)b(x) + a(x)c(x)

The element (01) = (00000001) is called the multiplicative identity. For any polynomial b(x) of degree less than 8, the multiplicative inverse of b(x), denoted by b−1(x), can be found by using the extended euclidean algorithm such that

b(x)a(x) + m(x)c(x) = 1

from which b(x)a(x) mod m(x) ≡ 1. Thus, the multiplicative inverse of b(x) becomes

b−1(x) = a(x)modm(x).

The set of 256 possible byte values has the structure of the ﬁnite ﬁeld GF(28) by means of XOR used as both addition and multiplication.

Multiplication by x

Let the binary polynomial be b(x)						=	7	b	xi . Multiplying b(x) by x results in xb(x)	=
							i=0
7	b	xi	+	1				i
					, but it can be reduced by modulo m(x).
i=0	i

If b7 = 1, the reduction is achieved by XORing m(x). It follows that implication by x (i.e. (00000010)(2) = (02)(16)) can be implemented at the byte level with a left shift and bitwise XOR with (1b). This operation on bytes is denoted by xtime(). Multiplication by higher powers of x can be implemented by repeated application of xtime().

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 1213 / 4313 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
21.11.2019368.64 Кб15inf_selfwork.doc
#
27.11.2019103.94 Кб14Institut_konfiskatsii_v_zarubezhnykh_stranakh.doc
#
28.02.2020325.12 Кб0instr.doc
#
10.02.201513.28 Mб31intel_v10_full_final.pdf
#
10.02.20156.96 Mб18InterAction_Noyabr_2013.pdf
#
10.02.20153.75 Mб43Internet.Security.pdf
#
12.01.202043.75 Кб0Inzhenernye_seti_i_OTZIS (1).docx
#
10.02.201588.58 Кб76inzhiniring.doc
#
28.12.2019312.83 Кб0iogp_otvety_k_ekzamenu.doc
#
22.12.2018128.51 Кб13iogp_zachet_1.doc
#
02.03.202088.06 Кб0IP_NIR_Magistranta.doc