
Internet.Security
.pdf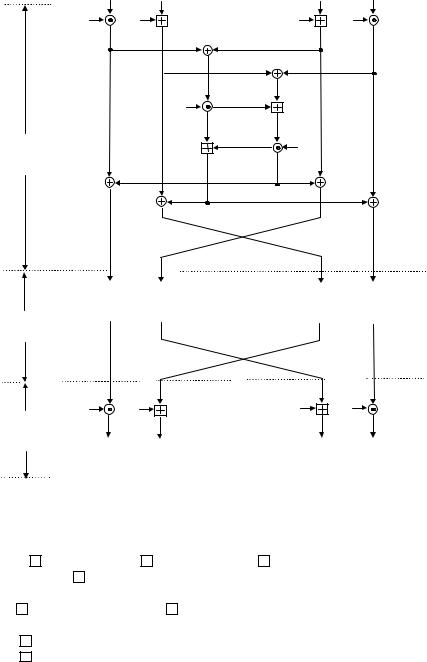
80 |
|
INTERNET SECURITY |
|
|
Plaintext X = (X1, X2, X3, X4) |
|
X1 |
X2 |
Z1 |
Z2 |
Z3 |
Z5
|
|
|
|
|
Y |
|
|
|
|
|
L |
Z6 |
|
Round 1 |
|
|
|
|
|
|
|
|
|
|
F |
|
|
|
|
|
|
M |
|
|
|
• |
A• |
|
|
||
|
T |
• |
|
|
|
|
|
• |
|
|
|
|
|
|
• |
|
• |
|
|
|
Seven more rounds |
|
E |
|
|
||
X3 X4
Z4
••
••
••
Z49 |
Z50 |
Z51 |
Z52 |
Output |
|
|
|
transformation |
|
|
|
stage |
Y2 |
Y3 |
Y4 |
Y1 |
|||
|
Ciphertext Y = (Y1, Y2, Y3, Y4) |
|
|
Figure 3.8 IDEA encryption scheme.
(8)(((X2 + Z2) (X4 Z4)) + (((X1 Z1) (X3 + Z3)) Z5)) = ((2) (4)) + (((1) (3)) Z5)
(9)(8) Z6
(10)(7) + (9) = (((1) (3)) Z5) + ((8) Z6)
(11)(X1 Z1) ((8) Z6) = (1) (9)
(12)(X3 + Z3) (9) = (3) (9)
(13)(X2 + Z2) (10) = (2) (10)
(14)(X4 Z4) (10) = (4) (10)
Team-Fly®

SYMMETRIC BLOCK CIPHERS |
81 |
The output of each round is the four sub-blocks that result from steps 11 – 14. The two inner blocks (12) and (13) are interchanged before being applied to the next round input. The final output transformation after the eighth round will involve the following steps:
(1)X1 Z49
(2)X2 + Z50
(3)X3 + Z51
(4)X4 Z52
where Xi, 1 ≤ i ≤ 4, represents the output of the eighth round. As you see, the final ninth stage requires only four subkeys, Z49, Z50, Z51 and Z52, compared to six subkeys for each of the first eight rounds. Note also that no swap is required for the two inner blocks at the output transformation stage.
Example 3.9 Assume that the 64-bit plaintext X is given as
X = (X1, X2, X3, X4) = (7fa9 1c37 ffb3 df05)
In the IDEA encryption, the plaintext is 64 bits in length and the encryption key consists of the 52 subkeys as computed in Example 3.8.
As shown in Figure 3.8, the four 16-bit input sub-blocks, X1, X2, X3 and X4, are XORed, added and multiplied with one another and with six 16-bit subkeys. Following the sequential operation starting from the first round through to the final transformation stage, the ciphertext Y = (Y1, Y2, Y3, Y4) is computed as shown in Table 3.11.
Table 3.11 Ciphertext computation through IDEA encryption rounds
|
|
|
Plaintext Input X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7fa9 |
1c37 |
ffb3 |
df05 |
|
|
(X1) |
(X2) |
(X3) |
(X4) |
|
|
|
|
|
|
|
Round |
Round output |
|
|
|
|
|
|
|
|
|
|
1 |
C579 |
F2ff |
0fbd |
0ffc |
|
2 |
D7a2 |
80cb |
9a61 |
27c5 |
|
3 |
ab6c |
e2f9 |
f3be |
36bd |
|
4 |
ef5b |
9cd2 |
6808 |
3019 |
|
5 |
7e09 |
2445 |
d223 |
d639 |
|
6 |
4a6e |
d7ac |
ac8c |
8b09 |
|
7 |
244d |
6f5c |
4459 |
3a9c |
|
8 |
0f86 |
7b0b |
54df |
759f |
← Ciphertext Y |
9 (final |
106b |
dbfd |
f323 |
0876 |
|
transformation) |
(Y1) |
(Y2) |
(Y3) |
(Y4) |
|

82 |
INTERNET SECURITY |
The ciphertext Y represents the output of the final transformation stage:
Y = (Y1, Y2, Y3, Y4) = (106b dbfd f323 0876)
3.2.3IDEA Decryption
IDEA decryption is exactly the same as the encryption process, except that the key subblocks are reversed and a different selection of subkeys is used. The decryption subkeys are either the additive or multiplicative inverse of the encryption subkeys. The decryption key sub-blocks are derived from the encryption key sub-blocks shown in Table 3.12.
Looking at the decryption key sub-blocks in Table 3.12, we see that the first four decryption subkeys at round i are derived from the first four subkeys at encryption round (10 − i), where the output transformation stage is counted as round 9. For example, the first four decryption subkeys at round 2 are derived from the first four encryption subkeys of round 8, as shown in Table 3.13.
Note that the first and fourth decryption subkeys are equal to the multiplicative inverse modulo (216 + 1) of the corresponding first and fourth encryption subkeys. For rounds 2 to 8, the second and third decryption subkeys are equal to the additive inverse modulo 216 of the corresponding subkeys’ third and second encryption subkeys. For rounds 1 and 9, the second and third decryption subkeys are equal to the additive inverse modulo 216 of
Table 3.12 IDEA encryption and decryption subkeys
|
Round |
Encryption subkeys |
Decryption subkeys |
|||||||
|
|
|
|
|
|
|||||
1 |
Z1 Z2 Z3 Z4 Z5 Z6 |
|
Z49−1 − Z50 − Z51Z52−1 Z47 Z48 |
|||||||
2 |
Z7 Z8 Z9 Z10 Z11 Z12 |
|
Z43−1 − Z45 − Z44Z46−1 Z41 Z42 |
|||||||
3 |
Z13 Z14 Z15 Z16 Z17 Z18 |
Z37−1 |
− |
Z39 |
− |
Z38Z40−1 Z35 Z36 |
||||
4 |
Z19 Z20 Z21 Z22 Z23 Z24 |
1 |
|
1 |
Z29 Z30 |
|||||
Z31− |
− Z33 |
− Z32Z34− |
||||||||
5 |
Z25 Z26 Z27 Z28 Z29 Z30 |
Z25−1 − Z27 |
− Z26Z28−1 Z23 Z24 |
|||||||
6 |
Z31 Z32 Z33 Z34 Z35 Z36 |
Z19−1 − Z21 |
− Z20Z22−1 Z17 Z18 |
|||||||
7 |
Z37 Z38 Z39 Z40 Z41 Z42 |
Z13−1 − Z15 |
− Z14Z16−1 Z11 Z12 |
|||||||
8 |
Z43 Z44 Z45 Z46 Z47 Z48 |
Z7−1 − Z9 − Z8 Z10−1Z5Z6 |
||||||||
|
9 |
Z49 Z50 Z51 Z52 |
|
Z1−1 − Z2 − Z3 Z4−1 |
|
|
||||
Table 3.13 Decryption subkeys derived from encryption subkeys |
|
|
||||||||
|
|
|
|
|
|
|||||
Round i |
First four decryption |
Round (10 − i) |
|
|
First four encryption |
|||||
|
|
subkeys at i |
|
|
|
|
|
subkeys at (10 − i) |
||
1 |
|
Z49−1 − Z50 − Z51 Z52−1 |
|
9 |
|
|
|
Z49 Z50 Z51 Z52 |
||
2 |
|
Z43−1 − Z45 − Z44 Z46−1 |
|
8 |
|
|
|
Z43 Z44 Z45 Z46 |
||
· |
|
|
|
· |
|
|
|
|
|
|
· |
|
|
|
· |
|
|
|
|
|
|
· |
|
Z7−1 − Z9 − Z8Z10−1 |
|
· |
|
|
|
|
|
|
8 |
|
|
2 |
|
|
|
Z7 Z8 Z9 Z10 |
|||
9 |
|
Z1−1 − Z2 − Z3Z4−1 |
|
1 |
|
|
|
Z1 Z2 Z3 Z4 |
||

SYMMETRIC BLOCK CIPHERS |
83 |
the corresponding second and third encryption subkeys. Note also that, for the first eight rounds, the last two subkeys of decryption round i are equal to the last two subkeys of encryption round (9 − i) (see Table 3.12).
Example 3.10 Using Table 3.12, compute the decryption subkeys corresponding to the encryption key sub-blocks obtained in Table 3.10. The IDEA decryption key is computed as shown in Table 3.14.
IDEA decryption is exactly the same as the encryption process, but the decryption subkeys are composed of either the additive or multiplicative inverse of the encryption subkeys, as indicated in Table 3.12.
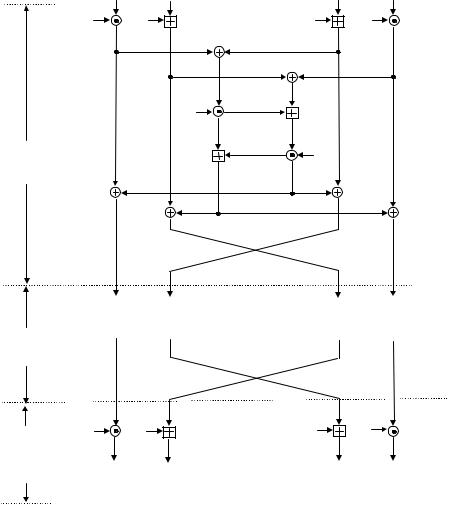
The IDEA decryption scheme for recovering plaintext is shown in Figure 3.9.
Example 3.11 Restore the plaintext X = (7fa9 1c37 ffb3 df05) using the ciphertext Y = (106b dbfd f323 0876) that was computed in Example 3.9.
The recovering steps are shown by the round-after-round process as indicated in Table 3.15.
Thus, the recovered plaintext is X = (X1, X2, X3, X4) = (7fa9 1c37 ffb3 df05).
Table 3.14 Subkey blocks for decryption
Z49−1 |
= |
9194 |
−Z26 |
= ff75 |
|
−Z50 = 78e2 |
Z28−1 = 24f6 |
||||
−Z51 |
= |
87e8 |
Z23 |
= ecf8 |
|
Z52−1 |
= |
712a |
Z24 |
= |
0871 |
Z47 |
= |
022f |
Z19−1 |
= |
4396 |
Z48 = 7fe0 |
−Z21 = 03f3 |
||||
Z43−1 |
= a24c |
−Z20 |
= ba11 |
||
−Z45 |
= f3f0 |
Z22−1 |
= dfa7 |
||
−Z44 |
= |
70c4 |
Z17 |
= e781 |
|
Z−1 |
= |
3305 |
Z18 |
= |
8205 |
46 |
|
1 |
|
||
Z41 = 6b42 |
Z13− |
= 18a7 |
|||
Z42 = 9f67 |
−Z15 = f94c |
||||
Z37−1 |
= c579 |
−Z14 |
= |
0802 |
|
−Z39 = f7ec |
Z16−1 = 9a13 |
||||
−Z38 = 61fa |
Z11 = c0c1 |
||||
Z40−1 |
= bf28 |
Z12 |
= |
028d |
|
Z35 = a14f |
Z7−1 = 55ed |
||||
1 |
= |
b3e0 |
− 9 |
= |
83fc |
Z36 |
|
Z |
|
||
Z31− |
= c53c |
−Z8 = 00fd |
|||
−Z33 |
= e841 |
Z10−1 |
= |
2cd9 |
|
−Z32 |
= fcfc |
Z5 |
= |
6081 |
|
Z34−1 |
= 3703 |
Z6 |
= |
46a0 |
|
Z29 = a7d9 |
Z1−1 = 0dd8 |
||||
Z30 |
= f010 |
−Z2 |
= 04c2 |
||
Z25−1 |
= cc14 |
−Z3 |
= fde4 |
||
Z |
= |
2008 |
Z−1 |
= |
4fd0 |
− 27 |
|
4 |
|
||
84 |
INTERNET SECURITY |
|
|
|
Ciphertext Y = (Y1, Y2, Y3, Y4) |
|
|
Y1 |
Y2 |
Y3 |
Y4 |
Z49−1 |
−Z50 |
−Z51 |
Z52−1 |
Z47
Z48
Round 1
• |
• |
• |
• |
• |
• |
• |
• |
• |
• |
• |
• |
Seven more rounds
Z1−1 |
−Z2 |
−Z3 |
Z4−1 |
Output |
|
|
|
transformation |
|
|
|
stage |
|
X3 |
X4 |
X1 |
X2 |
Plaintext X = (X1, X2, X3, X4)
Figure 3.9 IDEA decryption scheme.
3.3 RC5 Algorithm
The RC5 encryption algorithm was designed by Ronald Rivest of Massachusetts Institute of Technology (MIT) and it first appeared in December 1994. RSA Data Security, Inc. estimates that RC5 and its successor, RC6, are strong candidates for potential successors to DES. RC5 analysis (RSA Laboratories) is still in progress and is periodically updated to reflect any additional findings.

|
|
SYMMETRIC BLOCK CIPHERS |
85 |
|||
Table 3.15 Plaintext computation through IDEA decryption steps |
|
|
||||
|
|
Ciphertext Input Y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
106b |
dbfd |
f323 |
0876 |
|
|
|
(Y1) |
(Y2) |
(Y3) |
(Y4) |
|
|
|
|
|
|
|
|
|
Round |
|
Round output |
|
|
|
|
|
|
|
|
|
|
|
1 |
24e4 |
5069 |
fe98 |
dfd8 |
|
|
2 |
ffb1 |
b4a0 |
75b2 |
0b77 |
|
|
3 |
7420 |
e9e2 |
2749 |
00cc |
|
|
4 |
124c |
4800 |
9d5d |
9947 |
|
|
5 |
9c42 |
efcb |
28e8 |
70f9 |
|
|
6 |
ed80 |
a415 |
78c9 |
bdca |
|
|
7 |
dca8 |
8bc1 |
f202 |
48a6 |
|
|
8 |
3649 |
01cf |
1775 |
1734 |
→ Recovered |
|
9 (final |
7fa9 |
1c37 |
ffb3 |
df05 |
||
transformation) |
(X1) |
(X2) |
(X3) |
(X4) |
Plaintext X |
|
3.3.1Description of RC5
RC5 is a symmetric block cipher designed to be suitable for both software and hardware implementation. It is a parameterised algorithm, with a variable block size, a variable number of rounds and a variable-length key. This provides the opportunity for great flexibility in both performance characteristics and the level of security.
A particular RC5 algorithm is designated as RC5-w/r/b. The number of bits in a word, w, is a parameter of RC5. Different choices of this parameter result in different RC5 algorithms. RC5 is iterative in structure, with a variable number of rounds. The number of rounds, r, is a second parameter of RC5. RC5 uses a variable-length secret key. The key length b (in bytes) is a third parameter of RC5. These parameters are summarised as follows:
w: The word size, in bits. The standard value is 32bits; allowable values are 16, 32 and 64. RC5 encrypts two-word blocks so that the plaintext and ciphertext blocks are each 2w bits long.
r: The number of rounds. Allowable values of r are 0, 1, . . . , 255. Also, the expanded key table S contains t = 2 (r + 1) words.
b: The number of bytes in the secret key K. Allowable values of b are 0, 1, . . . , 255.
K: The b-byte secret key; K[0], K[1], . . . , K[b − 1]
RC5 consists of three components: a key expansion algorithm, an encryption algorithm and a decryption algorithm. These algorithms use the following three primitive operations:
1. + Addition of words modulo 2w
86 |
INTERNET SECURITY |
2.Bit-wise exclusive-OR of words
3.<<< Rotation symbol: the rotation of x to the left by y bits is denoted by x <<< y.
One design feature of RC5 is its simplicity, which makes RC5 easy to implement. Another feature of RC5 is its heavy use of data-dependent rotations in encryption; this feature is very useful in preventing both differential or linear cryptanalysis.
Example 3.12 Given RC5-32/16/10. This particular RC5 algorithm has 32-bit words, 16 rounds, a 10-byte (80-bit) secret key variable and an expanded key table S of t = 2(r + 1) = 2(16 + 1) = 34 words. Rivest proposed RC5-32/12/16 as a block cipher providing a normal choice of parameters, i.e. 32-bit words, 12 rounds, 16-byte (128-bit) secret key variable and an expanded key table of 26 words.
3.3.2 Key Expansion
The key-expansion algorithm expands the user’s key K to fill the expanded key table S, so that S resembles an array of t = 2(r + 1) random binary words determined by K. It uses two word-size magic constants Pw and Qw defined for arbitrary w as shown below:
Pw = Odd ((e − 2)2w )
Qw = Odd ((φ − 1)2w )
where
e = 2.71828 . . . (base of natural logarithms)
√
φ = (1 + 5)/2 = 1.61803 . . . (golden ratio) Odd(x) is the odd integer nearest to x.
First algorithmic step of key expansion: This step is to copy the secret key K[0, 1, . . . , b − 1] into an array L[0, 1, . . . , c − 1] of c = b/u words, where u = w/8 is the number of bytes/word.
This first step will be achieved by the following pseudocode operation: for i = b − 1 down to 0 do L[i/u] = (L[i/u] <<< 8) + K[i]; where all bytes are unsigned and the array L is initially zeroes.
Second algorithmic step of key expansion: This step is to initialise array S to a particular fixed pseudo-random bit pattern, using an arithmetic progression modulo 2w determined by two constants Pw and Qw.
S[0] = Pw:
for i = 1 to t − 1 do S[i] = S[i − 1] + Qw.
Third algorithmic step of key expansion: This step is to mix in the user’s secret key in three passes over the arrays S and L. More precisely, due to the potentially different sizes
SYMMETRIC BLOCK CIPHERS |
87 |
of S and L, the larger array is processed three times, and the other array will be handled more after.
i = j = 0;
A = B = 0;
do 3 max (t, c) times:
A = S[i] = (S[i] + A + B) <<< 3
B= L[j ] = (L[j ] + A + B) <<< (A + B); i = (i + 1) (mod t);
j = (j + 1) (mod c).
Note that with the key-expansion function it is not so easy to determine K from S, due to the one-wayness.
Example 3.13 Consider RC5-32/12/16. Since w = 32, r = 12 and b = 16, we have
u = w/8 = 32/8 = 4 bytes/word c = b/u = 16/4 = 4 words
t = 2(r + 1) = 2(12 + 1) = 26 words
The plaintext and the user’s secret key are given as follows:
Plaintext = eedba521 6d8f4b15
Key = 91 5f 46 19 be 41 b2 51 63 55 a5 01 10 a9 ce 91
1. Key expansion Two magic constants
P32 = 3084996963 = 0xb7e15163
Q32 = 2654435769 = 0x9e3779b9
Step 1
For i = b − 1 down to 0 do L[i/u] = (L[i/u] <<< 8) + K[i] where b = 16, u = 4 and L is initially 0.
L[i/4] = L[3] for i = 15, 14, 13 and 12.
L[3] = (L[3] <<< 8) + K[15] = 00 + 91 = 91
L[3] = (L[3] <<< 8) + K[14] = 9100 + ce = 91ce
L[3] = (L[3] <<< 8) + K[13] = 91ce00 + a9 = 91cea9
L[3] = (L[3] <<< 8) + K[12] = 91cea900 + 10 = 91cea910 L[i/4] = L[2] for i = 11, 10, 9 and 8.
L[2] = (L[2] <<< 8) + K[11] = 00 + 01 = 01
88 |
INTERNET SECURITY |
L[2] = (L[2] <<< 8) + K[10] = 0100 + a5 = 01a5
L[2] = (L[2] <<< 8) + K[9] = 01a500 + 55 = 01a555
L[2] = (L[2] <<< 8) + K[8] = 01a55500 + 63 = 01a55563 L[i/4] = L[1] for i = 7, 6, 5 and 4.
L[1] = (L[1] <<< 8) + K[7] = 00 + 51 = 51 L[1] = (L[1] <<< 8) + K[6] = 5100 + b2 = 51b2
L[1] = (L[1] <<< 8) + K[5] = 51b200 + 41 = 51b241
L[1] = (L[1] <<< 8) + K[4] = 51b24100 + be = 51b241be L[i/4] = L[0] for i = 3, 2, 1 and 0.
L[0] = (L[0] <<< 8) + K[3] = 00 + 19 = 19 L[0] = (L[0] <<< 8) + K[2] = 1900 + 46 = 1946
L[0] = (L[0] <<< 8) + K[1] = 194600 + 5f = 19465f
L[0] = (L[0] <<< 8) + K[0] = 19465f00 + 91 = 19465f91
Thus, converting the secret key from bytes to words (*) yields:
L[0] = 19465f91
L[1] = 51b241be
L[2] = 01a55563
L[3] = 91cea910
Step 2
S[0] = P32. For i = 1 to 25, do S[i] = S[i − 1] + Q32:
S[0] = b7e15163 |
|
S[1] = S[0] + Q32 |
= b7e15163 + 9e3779b9 = 5618cb1c |
S[2] = S[1] + Q32 |
= 5618cb1c + 9e3779b9 = f45044d5 |
S[3] = S[2] + Q32 |
= f45044d5 + 9e3779b9 = 9287be8e |
. |
. |
. |
. |
. |
. |
S[25] = S[24] + Q32 = 8f14babb + 9e3779b9 = 2b4c3474
When the iterative processes continue up to t − 1 = 2(r + 1) − 1 = 25, we can obtain the expanded key table S as shown below:
S[0] = b7e15163 |
S[09] = 47d498e4 |
S[18] = d7c7e065 |
S[1] = 5618cb1c |
S[10] = e60c129d |
S[19] = 75ff5a1e |
S[2] = f45044d5 |
S[11] = 84438c56 |
S[20] = 1436d3d7 |
S[3] = 9287be8e |
S[12] = 227b060f |
S[21] = b26e4d90 |
S[4] = 30bf3847 |
S[13] = c0b27fc8 |
S[22] = 50a5c749 |
S[5] = cef6b200 |
S[14] = 5ee9f981 |
S[23] = eedd4102 |
SYMMETRIC BLOCK CIPHERS |
89 |
||
S[6] = 6d2e2bb9 |
S[15] = fd21733a |
S[24] = 8d14babb |
|
S[7] = 0b65a572 |
S[16] = 9b58ecf3 |
S[25] = 2b4c3474 |
|
S[8] = a99d1f2b |
S[17] = 399066ac |
|
|
Step 3
i = j = 0; A = B = 0;
3 × max(t, c) = 3 × 26 = 78 times A = S[i] = (S[i] + A + B) <<< 3
B = L[j ] = (L[j ] + A + B) <<< (A + B) i = i + 1(mod 26)
j = j + 1(mod 4)
A = S[0] = (b7e15163 + 0 + 0) <<< 3
= b7e15163 <<< 3 = bf0a8b1d
B= L[0] = (19465f91 + bf0a8b1d) <<< (A + B)
=d850eaae <<< bf0a8b1d = db0a1d55
A= S[1] = (5618cb1c + bf0a8b1d + db0a1d55) <<< 3
=f02d738e <<< 3 = 816b9c77
B = L[1] = (51b241be + 816b9c77 + db0a1d55) <<< (A + B)
= ae27fb8a <<< 5c75b9cc = 7fb8aae2
A = S[2] = (f45044d5 + 816b9c77 + 7fb8aae2) <<< 3
= f5748c2e <<< 3 = aba46177
B= L[2] = (01a55563 + aba46177 + 7fb8aae2) <<< (A + B)
=2d0261bc <<< 2b5d0c59 = 785a04c3
A = S[3] = (9287be8e + aba46177 + 785a04c3) <<< 3
= b68624c8 <<< 3 = b4312645
B = L[3] = (91cea910 + b4312645 + 785a04c3) <<< (A + B)
= be59d418 <<< 2c8b2b08 = 59d418be
. . .
A= S[25] = (4e0d4c36 + f66a1aaf + 6d7f672f) <<< 3
=b1f6ce14, <<< 3 = 8fb670a5,
B= L[1] = (cdfc2657 + 8fb670a5 + 6d7f672f) <<< (A + B)
=cb31fe2b <<< fd35d7d4 = e2bcb31f
