Расчетно-графическая работа №6 Тема: «Расчет числовых характеристик графов».

1. Теоретическая часть

Пусть задан граф G (рисунок 6.1).

Рисунок 6.1 ― ГрафG

Расчет количества вершин n(G) графа G

Расчет выполняется методом визуального анализа графа G. В итоге расчета имеем:

Расчет количества ребер m(G) графа G

Расчет выполняется методом визуального анализа графа G. В итоге расчета имеем:

Расчет степеней вершин δ_i графа G.

Расчет выполняется методом визуального анализа графа G с целью определения количества ребер (дуг) инцидентных вершине x_i. Результаты расчета сведены в таблицу 6.1.

Таблица 6.1 - Результаты расчета степеней вершин графа G

xi	δi
1	2
2	2
3	2
4	2
5	3
6	2
7	5
8	2
9	2

Расчет числа компонент связности æ(G)

Д

ля расчета числа компонент связности графаG вычисляют матрицу достижимости ||Q^p|| и определяют полные подграфы графа. Для построения матрицы достижимости удобно воспользоваться матрицей смежности графа G:

где ||1|| - единичная матрица (рисунок 6.2),

||H(x_i)|| - матрица смежности графа G,

||H^p(x_i)|| - матрица смежности графа G, возведенная в p-ую степень.

1	1	2	3	4	5	6	7	8	9
1	1	0	0	0	0	0	0	0	0
2	0	1	0	0	0	0	0	0	0
3	0	0	1	0	0	0	0	0	0
4	0	0	0	1	0	0	0	0	0
5	0	0	0	0	1	0	0	0	0
6	0	0	0	0	0	1	0	0	0
7	0	0	0	0	0	0	1	0	0
8	0	0	0	0	0	0	0	1	0
9	0	0	0	0	0	0	0	0	1

Рисунок 6.2 ― Единичная матрица для графа G

Для возведения в степень матрицы смежности используют правило умножения булевых матриц.

На рисунке 6.3 правило умножения булевых матриц прокомментировано графически.

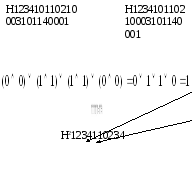
Первая строка на второй столбец

Обозначения: - дизъюнкция (см. таблицу истинности в [1] );- конъюнкция (см. таблицу истинности в [1])

Рисунок 6.3 ― Пример умножения булевых матриц 4х4

Построим матрицы смежности графа G (рисунок 6.4).

H	1	2	3	4	5	6	7	8	9
1	0	1	1	0	0	0	0	0	0
2	1	0	1	0	0	0	0	0	0
3	1	1	0	0	0	0	0	0	0
4	0	0	0	0	1	0	1	0	0
5	0	0	0	1	0	1	1	0	0
6	0	0	0	0	1	0	1	0	0
7	0	0	0	1	1	1	0	1	1
8	0	0	0	0	0	0	1	0	1
9	0	0	0	0	0	0	1	1	0

Рисунок 6.4 ― Матрица смежности ||H|| графа G

Возведем матрицу смежности ||H|| в квадрат, т.е. умножим ее саму на себя. Получим ||H²|| (рисунок 6.5).

H2	1	2	3	4	5	6	7	8	9
1	1	1	1	0	0	0	0	0	0
2	1	1	1	0	0	0	0	0	0
3	1	1	1	0	0	0	0	0	0
4	0	0	0	1	1	1	1	1	1
5	0	0	0	1	1	1	1	1	1
6	0	0	0	1	1	1	1	1	1
7	0	0	0	1	1	1	1	1	1
8	0	0	0	1	1	1	1	1	1
9	0	0	0	1	1	1	1	1	1

Рисунок 6.5 ― Матрица ||H²|| графа G

Возведем матрицу смежности ||H|| в третью степень. Получим ||H³|| (рисунок 6.6).

H3	1	2	3	4	5	6	7	8	9
1	1	1	1	0	0	0	0	0	0
2	1	1	1	0	0	0	0	0	0
3	1	1	1	0	0	0	0	0	0
4	0	0	0	1	1	1	1	1	1
5	0	0	0	1	1	1	1	1	1
6	0	0	0	1	1	1	1	1	1
7	0	0	0	1	1	1	1	1	1
8	0	0	0	1	1	1	1	1	1
9	0	0	0	1	1	1	1	1	1

Рисунок 6.6 ― Матрица ||H³|| графа G

Анализ матриц ||H²|| и ||H³|| показывает, что никаких изменений в ||H³|| по сравнению ||H²|| нет. Значит процесс вычислений завершен.

Матрица достижимости ||Q³|| (рисунок 6.7) рассчитывается следующим образом:

Q2	1	2	3	4	5	6	7	8	9
1	1	1	1	0	0	0	0	0	0
2	1	1	1	0	0	0	0	0	0
3	1	1	1	0	0	0	0	0	0
4	0	0	0	1	1	1	1	1	1
5	0	0	0	1	1	1	1	1	1
6	0	0	0	1	1	1	1	1	1
7	0	0	0	1	1	1	1	1	1
8	0	0	0	1	1	1	1	1	1
9	0	0	0	1	1	1	1	1	1

Рисунок 6.7 ― Матрица ||Q²|| графа G

Поскольку матрица ||Q²|| содержит два блока: один – 3х3 элемента, другой – 6х6 элементов, то граф G содержит два связных подграфа:

G₁=<X₁, H₁>, G₂=<X₂, H₂>,

где X₁={x₁,x₂,x₃}, X₂={x₄,x₅,x₆,x₇,x₈,x₉}.

Таким образом, для исходного графа G=<X,H> число компонент связности равно æ(G)=2.

Расчет цикломатического числа λ(G) графа G

Рассчитаем цикломатическое число графа G, т.е. наименьшее число ребер, удаление которых приведет к графу без циклов и петель.

Расчет выполним по формуле:

.

В качестве примера удалим на графе G четыре ребра (1,3), (4,5), (5,6), (8,9). Получим граф на рисунке 6.8.

Рисунок 6.8 ― Граф без циклов и петель

Расчет хроматического числа γ(G) графа G

Рассчитаем хроматическое число графа G, т.е. наименьшее число красок при применении которых для раскраски вершин графа две любые смежные вершины графа G, не будут окрашены в один цвет.

Для выполнения расчета воспользуемся двумя оценочными соотношениями. Одно из них задает левую границу для γ(G), min возможное значение γ(G), т.е. γ_min(G):

1. полный n-вершинный граф имеет γ_min(G)=n;

2. пустой граф имеет γ_min(G)=1;

3. граф с циклом (т.е. хотя бы одним) четной длины имеет γ_min(G)=2;

4. граф с циклом нечетной длины имеет γ_min(G)=3;

5. граф-дерево имеет γ_min(G)=2.

Другое оценочное соотношение задает правую границу для γ(G), max необходимое значение γ(G), т.е. γ_max(G):

.

Начинаем проверку с вычисления γ_min(G). Поскольку в графе G есть цикл нечетной длины пробуем раскрасить граф тремя красками (рисунок 6.9).

Рисунок 6.9 ― Раскраска графа G синей, желтой и красной красками

Вывод: трех красок, т.е. γ_min(G)=3 оказалось достаточно:

.

Если бы трех красок оказалось недостаточно, следовало бы γ_min(G) увеличить на единицу и повторить раскраску заново. И так далее, до получения желаемого результата. Однако таких красок не должно быть больше чем γ_max(G).

Расчет плотности (G) графа G

Рассчитаем плотность графа G, т.е. наибольшее число вершин подграфа графа G, между всеми вершинами которого задано отношение смежности.

Получим матрицы смежности ||H|| и достижимости ||Q|| графа G (рисунок 6.10).

H	4	5	6	7	8	9
4	0	1	0	1	0	0
5	1	0	1	1	0	0
6	0	1	0	1	0	0
7	1	1	1	0	1	1
8	0	0	0	1	0	1
9	0	0	0	1	1	0

Q	4	5	6	7	8	9
4	1	1	0	1	0	0
5	1	1	1	1	0	0
6	0	1	1	1	0	0
7	1	1	1	1	1	1
8	0	0	0	1	1	1
9	0	0	0	1	1	1

Рисунок 6.10 ― Матрицы ||H|| и ||Q|| графа G

В матрице || Q|| сформируем блоки, используя метод визуального анализа и перестановок строк (т.е. стоки меняются местами) и перестановок столбцов (т.е. столбцы меняются местами). В итоге получим матрицу ||Q|| на рисунке 6.11.

Q	8	9	7	4	5	6
8	1	1	1	0	0	0
9	1	1	1	0	0	0
7	1	1	1	1	1	1
4	0	0	1	1	1	0
5	0	0	1	1	1	1
6	0	0	1	0	1	1

Рисунок 6.11 ― Матрица || Q || с тремя выделенными блоками

Анализ матрицы || Q || на рисунке 6.11 показывает, что поскольку число блоков равно трем, то имеем три полных подграфа G с тремя вершинами в каждом (1-ый блок: 3х3, 2-ой блок: 3х3, 3-ий блок: 2х2). Иными словами, |Х`<sub>1</sub>|=3, |Х`₂|=3, |Х`₃|=2 (рисунок 6.12).

Рисунок 6.12 ― Три подграфа графа G

Обозначения: пунктиром выделены полные подграфы графа G.

Таким образом имеем:

.

Расчет неплотности ε(G) графа G

Рассмотрим плотность графа G, т.е. наибольшее число вершин пустого подграфа графа G между всеми вершинами которого нет отношений смежности.

Построим обратный граф ┐G для графа G. Для этого получим матрицу || H || и обратную ей матрицу || ┐H || (рисунок 6.13).

H	4	5	6	7	8	9
4	0	1	0	1	0	0
5	1	0	1	1	0	0
6	0	1	0	1	0	0
7	1	1	1	0	1	1
8	0	0	0	1	0	1
9	0	0	0	1	1	0

┐H	4	5	6	7	8	9
4	1	0	1	0	1	1
5	0	1	0	0	1	1
6	1	0	1	0	1	1
7	0	0	0	1	0	0
8	1	1	1	0	1	0
9	1	1	1	0	0	1

Рисунок 6.13 ― Матрицы смежности (слева-направо) графа G и графа ┐G

Строим матрицу достижимости графа ┐G и выполняем операцию перестановки строк и столбцов. Результаты показаны на рисунке 6.14.

┐Qp	9	6	4	8	5	7
9	1	1	1	0	1	0
6	1	1	1	1	0	0
4	1	1	1	1	0	0
8	0	1	1	1	1	0
5	1	0	0	1	1	0
7	0	0	0	0	0	1

┐Qp	4	5	6	7	8	9
4	1	0	1	0	1	1
5	0	1	0	0	1	1
6	1	0	1	0	1	1
7	0	0	0	1	0	0
8	1	1	1	0	1	0
9	1	1	1	0	0	1

Рисунок 6.14 ― Матрицы достижимости ┐Q^p графа ┐G

Примечание: матрица на рисунке справа имеет блочную структуру.

На рисунке 6.15 показан обратный граф ┐G.

Рисунок 6.15 - Обратный граф ┐G

Анализ матрицы ┐Q^p с блочной структурой на рисунке 6.14 показывает, что поскольку число блоков – три, то имеем три пустых подграфа графа G (рисунок 6.16):

|Х`<sub>1</sub>|=3, |Х`₂|=3, |Х`₃|=2.

Рисунок 6.16 - Три пустых подграфа графа G

Таким образом имеем:

.

Расчет внешней устойчивости ψ(G) графа G

Рассчитаем внешнюю устойчивость графа G, т.е. наименьшее число вершин графа G смежных со всеми остальными вершинами графа.

Составим таблицу 6.2 отображений для графа G и дополним ее столбцом несмежных вершин.

Таблица 6.2 ― Таблица отображений графа G

xi	Hi	┐Hi
4	5,7	6,8,9
5	4,6,7	8,9
6	5,7	4,8,9
7	4,5,6,8,9
8	7,9	4,5,6
9	7,8	4,5,6

Анализ таблицы 6.2 показывает, что в столбце ┐H_i есть несмежные вершины. В этом случае необходимо построить еще одну таблицу – таблицу 6.3 следующим образом.

Таблица 6.3 строится на базе строк таблицы 6.2, в которых нет знака в столбце ┐H_i. В нашем случае таких строк – пять. В строках первого столбца таблицы 6.3 пары вершин, образованные полным перебором вершин из первого и второго столбцов таблицы 6.2. В строках второго и третьего столбцов таблицы 6.3 указываются смежные и несмежные вершины, соответственно, для {х_i,х_j}, перечисляемых в строках первого столбца таблицы 6.3.

Таблица 6.3 ― Таблица отображений и несмежных вершин для двухэлементных подмножеств

{xi,xj}	H(xi,xj)	┐H(xi,xj)
x4,x5	x6,x7	x8,x9
x4,x7	x5,x6,x8,x9
x5,x6	x4x7	x8,x9
x5,x7	x4,x6,x8,x9
x7,x6	x5,x8,x9	x4
x7,x8	x4,x5,x6,x9
x7,x9	x4,x5,x6,x8
x8,x9	x7	x4,x5,x6

Если в таблице 6.3 найдется , т.е. хотя бы в одной строке столбца 3 таблицы 6.3 будет стоять знак, то расчеты завершены. В противном случае необходимо перейти к формированию новых таблиц отображений и несмежных вершин для трех элементных подмножеств, т.е.H(x_i,x_j,x_k) и ┐H(x_i,x_j,x_k) и т.д.

В нашем примере во второй, четвертой, шестой и седьмой строках стоят знаки . Значит расчеты закончены и можно приступать к анализу таблицы 6.2 и таблицы 6.3.

По итогам анализа таблицы 6.3 можно сформировать множество T потенциальных ядер графа G, т.е.

Т= {{ x₄,x₅},{ x₄,x₇},{x₇,x₈},{x₇, x₄}},

где T₁={ x₄,x₅}, T₂={x₅,x₇}, T₃={x₇,x₈}, T₄={x_7, x₄}.

Тогда ψ(G)={||}=||}|_i=1;4=2.

Расчет числа внутренней устойчивости (G) графа G

Составим таблицу 6.2 отображений и несмежных вершин графа G. Анализ таблицы 6.2 показывает, что в столбце ┐H_i есть несмежные вершины. В этом случае построим таблицу 6.4 двухэлементных множеств из несмежных вершин, найдем им образ и ┐.

Таблица 6.4 - Таблица образов и ┐

{xi,xj}		┐
4,6	5,7	8,9
4,8	5,7,9	6,9
4,9	5,7,8	6
5,8	4,6,7,9
5,9	4,6,7,8
6,8	5,7,9	4
6,9	5,7,8	4

Поскольку не во всех строках столбца ┐таблицы 6.4 указаны знаки, сформируем таблицу 6.5 трехэлементных множеств {x_i,x_j,x_k} и найдем им образи ┐.

Таблица 6.5 - Таблица образов и┐

{xi,xj,xk}		┐
4,6,8	5,7,9
4,6,9	5,8,7

Поскольку во всех строках таблицы 5.5 указаны знаки процесс вычислений закончен и можно перейти к анализу таблицы 6.4 и таблицы 6.5.

По итогам анализа можно сформировать множество S ядер графа G, т.е.

S={{x₅,x₈},{x₅,x₄},{x₄,x₆,x_8,},{x₄,x₆,x₉}},

где S₁={x₅,x₈}, S₂={x₅,x₉}, S₃={x₄,x₆,x₈}, S₄={x₄x₆,x₆}.

Тогда

(G)={|S_i|}={||}|_i=1;4=3.

На этом расчеты числовых характеристик графа G закончены.

2. Решение задач

Тема: «Графы. Основные понятия. Способы задания. Части графа»

Задачи для решения в аудитории

1. На рис. изображены графы с четырьмя вершинами в каждом. Сравнить графы.

2. Задать различными способами графы , представленные на рисунке ниже. Вычислить степени и полустепени вершин.

3. Для графов из задачи 2 построить полный граф, пустой граф, частичный граф, суграф, подграф, остов графа. Являются ли графыпланарными?

4. Пусть неориентированный и ориентированный графы ина рисунке ниже. задают отношение, т.е.и. Каковы свойства отношения?

Домашнее задание

1. Какие графы в задаче 10 являются деревьями? Какие графы в задаче 10 являются полными? Постройте остов для каждого графа из задачи10.

2. Построить мультиграф и полный граф для графов, заданных в задаче 5.

3. Изобразите неориентиованный, ориентированный и смешанный графы.

4. Определить степени и полустепени вершин для графов, заданных в задаче 5.

5. Задать графы множествами их вершин и ребер. Сравнить графы.

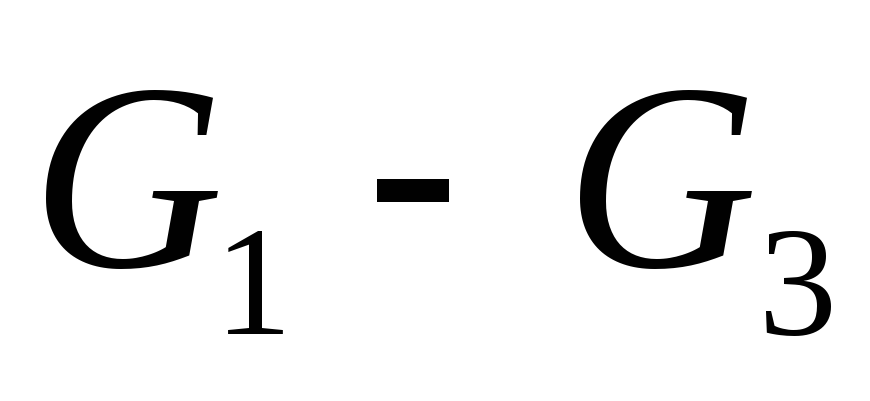6. Равны ли графына рисунке ниже. Задать графымножествами их вершин и ребер. Сравнить графы.

7. Определить дополнение графа, если: 1) граф- пятиугольник, 2) граф- треугольник.

8. Для графа на рисунке ниже построить: частичный граф, подграф и суграф.

9. Когда граф называется полностью заданным? Задайте граф в форме отображений.

10. Построить матрицы смежности и инциденции графов, изображенных на рисунке ниже. Чему равны степени вершин?

3. Задание

Задание на РГР формулируется следующим образом: «Найти основные числа графа G по данным, приведенным в таблице 6.6 для модели графа, представленной на рисунке 6.17: число вершин, число ребер, степени всех вершин, число компонент связности, цикломатическое число, хроматическое число, плотность и неплотность графа, числа внешней и внутренней устойчивости».

Рисунок 6.17 - Модель графа G

Таблица 6.6 - Данные для формирования графа G по вариантам

Номер варианта	Удалить в модели графа вершины {i}	Удалить в модели графа ребра {(i,j)}
1	{1,2}	{(4,7),(6,7),(7,8),(7,10),(10,11),(10,13)}
2	{1,2}	{(6,7),(7,10),(7,12),(10,11),(10,13),(11,12)}
3	{1,2}	{(6,7),(4,7),(4,8),(7,10),(10,11),(10,13)}
4	{1,2}	{(6,7),(7,10),(7,12),(8,12),(10,11),(10,13)}
5	{1,2}	{(4,8),(6,7),(7,8),(7,10),(10,11),(10,13)}
6	{2,5}	{(3,7),(4,7),(4,8),(4,9),(7,10),(7,11)}
7	{2,5}	{(3,7),(4,7),(4,8),(4,9),(7,12),(8,12)}
8	{2,5}	{(3,7),(4,7),(4,8),(4,9),(7,10),(10,11)}
9	{2,5}	{(3,7),(4,7),(4,8),(4,9),(7,12),(11,12)}
10	{2,5}	{(3,7),(4,7),(4,8),(4,9),(7,11),(10,11)}
11	{5,10}	{(2,7),(3,7),(7,11),(7,12),(8,12),(9,12)}
12	{5,10}	{(4,7),(4,8),(7,11),(7,12),(8,12),(9,12)}
13	{5,10}	{(2,3),(2,7),(7,11),(7,12),(8,12),(9,12)}
14	{5,10}	{(3,4),(4,7),(7,10),(7,12),(8,12),(9,12)}
15	{5,10}	{(2,3),(3,7),(7,10),(7,12),(8,12),(9,12)}

Таблица 6.6 - Продолжение

Номер варианта	Удалить в модели графа вершины {i}	Удалить в модели графа ребра {(i,j)}
16	{10,13}	{(1,2),(2,3),(2,7),(6,7),(7,8),(7,12)}
17	{10,13}	{(1,2),(2,3),(2,7),(3,4),(4,7),(6,7)}
18	{10,13}	{(1,2),(2,3),(2,7),(6,7),(7,12),(8,12)}
19	{10,13}	{(1,2),(2,3),(2,7),(4,7),(4,8),(6,7)}
20	{10,13}	{(1,2),(2,3),(2,7),(6,7),(7,8),(8,12)}
34	{1,4}	{(6,10),(7,8),(7,10),(7,12),(11,12),(12,13)}
35	{1,4}	{(2,6),(6,7),(7,8),(7,12),(11,12),(12,13)}
36	{12,13}	{(1,4),(3,4),(4,7),(6,7),(7,8),(7,10)}
37	{12,13}	{(1,4),(2,3),(2,7),(3,4),(4,7),(7,8)}
38	{12,13}	{(1,4),(3,4),(4,7),(6,10),(7,8),(7,10)}
39	{12,13}	{(1,4),(2,6),(2,7),(3,4),(4,7),(7,8)}
40	{12,13}	{(1,4),(3,4),(4,7),(6,7),(6,10),(7,8)}
41	{6,8}	{(3,7),(5,10),(7,10),(7,11),(7,12),(9,12)}
42	{6,8}	{(2,3),(5,10),(7,10),(7,11),(7,12),(9,12)}
43	{6,8}	{(1,3),(5,10),(7,10),(7,11),(7,12),(9,12)}
44	{6,8}	{(3,4),(5,10),(7,10),(7,11),(7,12),(9,12)}
45	{6,8}	{(5,10),(7,10),(7,11),(7,12),(9,12),(11,13)}
46	{3,11}	{(1,2),(2,7),(4,8),(6,7),(7,10),(10,13)}
47	{3,11}	{(1,2),(2,7),(6,7),(7,8),(7,10),(10,13)}
48	{3,11}	{(1,2),(2,7),(6,7),(7,10),(8,12),(10,13)}
49	{3,11}	{(1,2),(2,7),(6,7),(7,10),(8,9),(10,13)}
50	{3,11}	{(1,2),(2,7),(5,6),(6,7),(7,10),(10,13)}
51	{2,9}	{(6,7),(7,10),(7,12),(10,11),(10,13),(11,12)}
52	{2,9}	{(6,7),(7,8),(7,10),(7,12),(10,11),(10,13)}
53	{2,9}	{(6,7),(7,8),(7,10),(10,11),(10,13),(11,13)}
54	{2,9}	{(3,4),(4,7),(6,7),(7,10),(10,11),(10,13)}
55	{2,9}	{(4,7),(6,7),(7,8),(7,10),(10,11),(10,13)}
56	{9,10}	{(1,2),(2,3),(2,7),(3,4),(4,7),(6,7)}
57	{9,10}	{(1,2),(2,3),(2,7),(4,7),(6,7),(7,8)}
58	{9,10}	{(1,2),(2,3),(2,7),(6,7),(7,8),(7,12)}
59	{9,10}	{(1,2),(2,3),(2,7),(6,7),(7,12),(11,12)}
60	{9,10}	{(1,2),(2,3),(2,7),(3,4),(6,7),(7,8)}

4. Содержание отчета

1. Условие задачи в соответствии с вариантом.

2. Определение числа вершин.

3. Определение числа ребер.

4. Определение степени всех вершин.

5. Определение числа компонент связности.

6. Определение цикломатического числа.

7. Определение хроматического числа.

8. Определение плотности и неплотность графа.

9. Определение числа внешней и внутренней устойчивости.

Вычисление всех числовых характеристик графа расписать подробно по этапам.

5. Список литературы

1. Пономарев В.Ф. Дискретная математика для инженеров.- Калининград: ФГОУ ВПО КГТУ, 2010.- 351 с.