Практикум 1 по математическому анализу

Задание 3.

Найти частные производные второго порядка функции многих переменных.

Первые производные:

Вторые производные:

Задание 4.

Найти экстремумы функции двух переменных.

В соответствии с достаточным условием экстремума функции двух переменных найдем точки, удовлетворяющие условию:

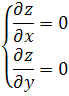
Частные производные первого порядка от функции z:

Приравняем их к нулю:

Решим систему уравнений:

Получаем 2 точки

Установим наличие экстремума функции z в точке . Для этого вычислим значения вторых производных и определим знак дискриминанта ∆ в точке .

Так как дискриминант равен нулю, вопрос о наличии экстремума в точке остается открытым.

Вычислим значения вторых производных и определим знак дискриминанта ∆ в точке :

Так как дискриминант равен нулю, вопрос о наличии экстремума в точке остается открытым.