Министерство транспорта РФ
Росморречфлот
ФГБОУ ВО «Сибирский Государственный
Университет
Водного Транспорта
»
Кафедра Теоретической и Прикладной Механики
КУРСОВАЯ РАБОТА
«Применение методов теоретической механики
к анализу движения и взаимодействия
материальных тел»
Вариант №4
Выполнил: Вафеев И.М
студент гр.З-ЭСЭУ-21
Проверил: Ратничкин А.А
К.ф.-м.н., доцент
Новосибирск 2019г.
Введение
Механика имеет отношение практически ко всем явлениям природы и творе-ниям техники, ко всем естественным научным дисциплинам. По существу, ни одно явление природы невозможно понять без уяснения его механической стороны и ни одно творение техники нельзя создать, не принимая в расчет те или иные закономерности. И в этом нет ничего удивительного, так как любое явление в окружающем нас мире связано с движением.
Теоретическая механика является одной из важнейших изучаемых в техни-ческих вузах физико-математических дисциплин, которой отводится важная роль в подготовке инженеров любых специальностей.
Значимость теоретической механики в инженерном образовании определя-ется тем, что эта дисциплина является фундаментом, на котором строится преподавание всех инженерных дисциплин, изучаемых в вузе. На основных законах, теоремах, принципах теоретической механики строятся выводы, доказательства во многих общеинженерных дисциплинах, например, таких, как сопротивление материалов, строительная механика, гидравлика, теория механизмов и машин, детали машин и т. п., они лежат в основе решения многих инженерных задач и с их помощью осуществляется проектирование новых машин, конструкций и сооружений.
Усвоение курса теоретической механики требует не только глубокого изучения теории, но и приобретения навыков решения задач.
1. Равновесие системы тел с учетом трения.
1.1 Основные сведения и теории: условия равновесия; трения сцепления; метод расчленения.
Равновесие системы сил с учетом трения
При стремлении сдвинуть одно тело по поверхности другого в касательной плоскости поверхностей этих тел возникают силы, препятствующие движению. Это явление называется трение. Различают трение покоя, трение движения и трение качения.
При трении покоя величина силы трения зависит от действующих на тело активных сил и может изменяться от нуля до некоторого своего наибольшего значения. Сила трения покоя, любое превышение которой ведет к возник-новению движения, называется наибольшей силой трения покоя.
Величина этой силы, имеющей место в предельном положении покоя тела, определяется по формуле, FТР.MAX=f·N
где f– коэффициент сцепления; N– сила нормального давления, прижимаю-щая тела друг к другу.
Трение двух тел, находящихся в относительном движении, называется трением движения.
Метод решения задач.
Существуют два случая решения задач на равновесие системы тел методом расчленения:
а) Конструкцию расчленяют на отдельные тела и составляют условия рав-новесия каждого тела в отдельности;
б) Сначала рассматривают равновесие всей конструкции целиком, а затем равновесие какой-нибудь одной или нескольких частей конструкции.
1.2 Задача С2 из (3).
Метод расчленения
Определить минимальное значение силы Р и реакцию опор системы, находя-щейся в покое.
Определить минимальное значение силы Р и реакции опор О и А. Весом рычага АВ, колодку и нити пренебречь. Коэффициент трения между колодкой и ступенчатым барабаном равен f=0,25; размеры : a=0,10m; b=0,40m; e=0,06m. Минимальное значение силы P соответствует предель-ному состоянию равновесия. Q=15kH; G=1,8kH, где G - вес барабана,
е - толщина колодки, Q – вес груза.
Решение:
Рассмотрим в равновесии по отдельности части конструкции и приложенные к ним силы
Расчетная схема 1.
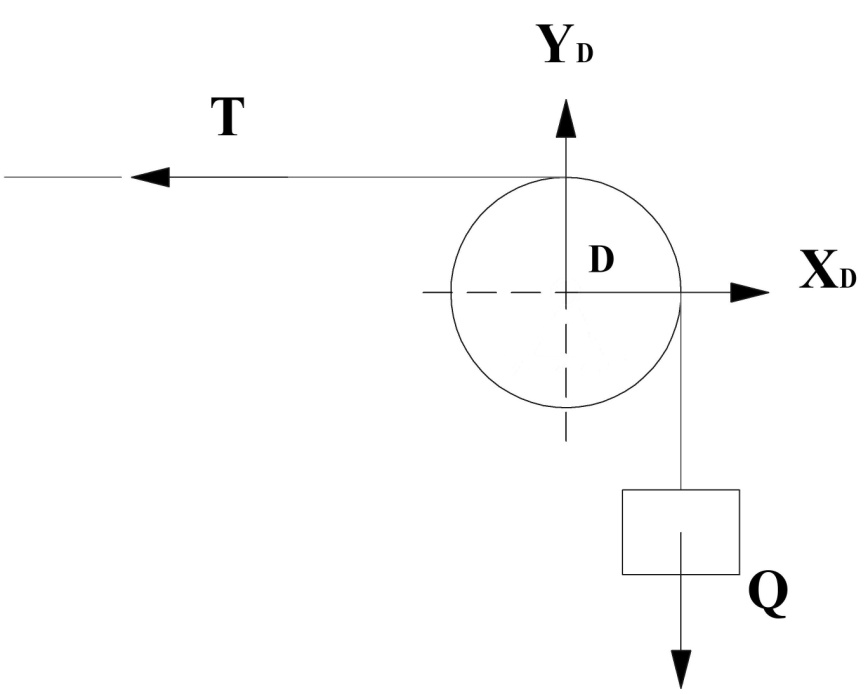
1.
а) ∑Xn =0
б) ∑Yn =0
в) ∑MO(Fn) =0
Из уравнения «в» находим T и Q
T=Q=15kH
XD=T=15kH
YD=15kH
Расчетная схема 2.
2.
а) ∑XO =0
б) ∑YO =0
в) ∑ MO(Fn) =0
Из уравнения «в» находим силу трения
FТР.MAX=T/2=7,5kH
После чего находим нормальную реакцию N:
FТР.MAX=f·N откуда: N= FТР.MAX/f=7,5/0,25=30kH
XO=30-7,5=22,5kH
YO=30+1,8=31,8kH
Расчетная схема 3.
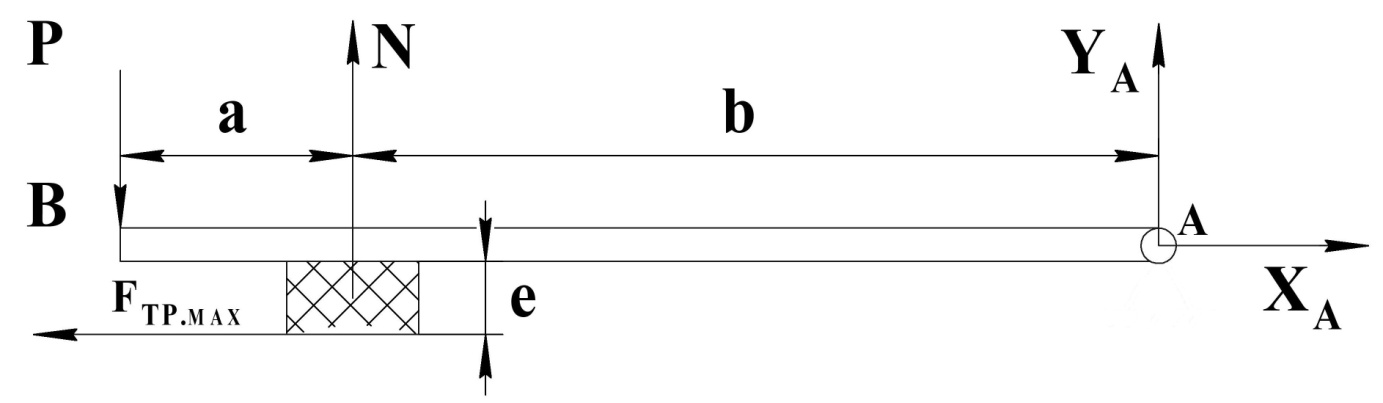
3.
а) ∑XA= XA- FТР.MAX=0
б) ∑YA= YA-Pmin+N=0
в) ∑ MO(Fn)=-N·B·Pmin(a+b)-FТР.MAX·e=0
Из уравнения «а»: XA=- FТР.MAX=7,5kH
Из уравнения «в» находим минимальное значение силы Р
Pmin=(N·b+ FТР.MAX·e)/(a+b)=(30·0,4+7,5·0,06)/0,5=24,9kH
После чего из уравнения «б» находим YA:
YA=30-24,9=5,1kH
Ответ: Pmin=24,9kH; XA=7,5kH; XO=22,5kH; YO=31,8kH; YA=5,1kH; FТР.MAX=7,5kH; N=30kH.
2. Определение положения центра тяжести однородного тела.
2.1 Основные сведения о методах нахождения ЦТ тел.
Силы
тяжести частей тела с некоторым допущением
можно считать параллельными, а их
совокупность принимать за систему
параллельных сил тяжести, эквивалентную
равнодействующей
,
называемой
силой
тяжести тела. {P̅i,..
.,P̅n}~P̅,
P̅=
Центр тяжести – геометрическая точка, в которой прикладывается сила тяжести, и которая зафиксирована относительно тела при любом его положе-нии в пространстве.
Координаты центра тяжести тела
Положение центров тяжести однородных тел зависит только от их формы, поэтому предыдущие формулы можно заменить в виде
Метод разбиения – тело разбивается на конечное число частей с известны-ми центрами тяжести. Координаты центра тяжести всего тела можно непос-редственно вычислить по выше приведённым формулам. При этом число слогаемых в каждой из сумм будет равно числу частей, на которое разбито тело.
2.2 Задача С3 из (3)
Определить положение центра тяжести однородного тела.
Решение:
1) Находим координаты центров фигур.
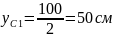
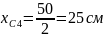
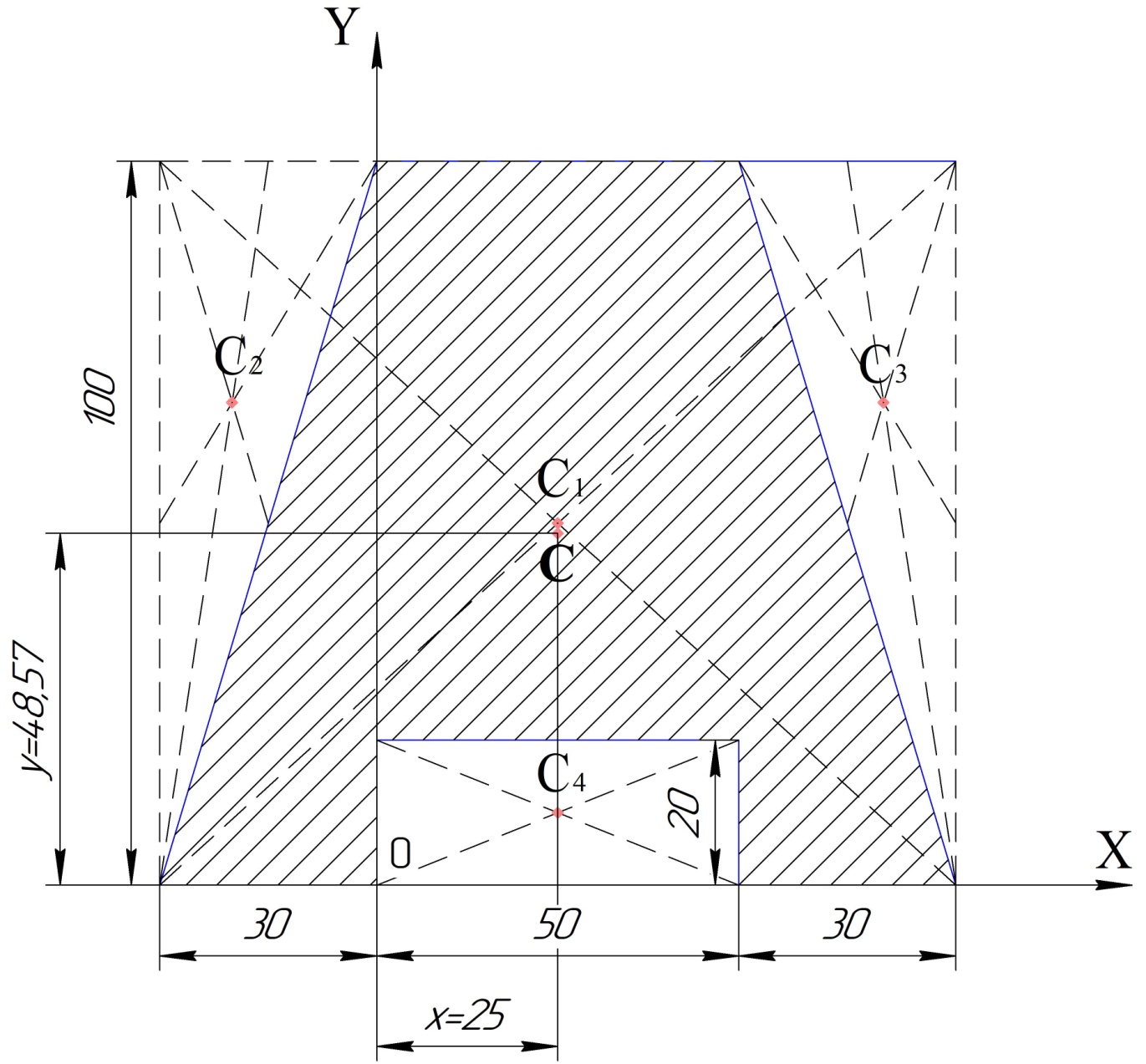
2) Находим площади фигур.
SC1=(50+30+30)·100=11000см2
SC2=-30·100/2=-1500см2
SC3=-30·100/2=-1500см2
SC4=-20·50=-1000см2
3) Находим координаты:
Ответ: XC=25 см
yC=48,57