
Курсовая работа по термеху курс2 шифр4
.pdf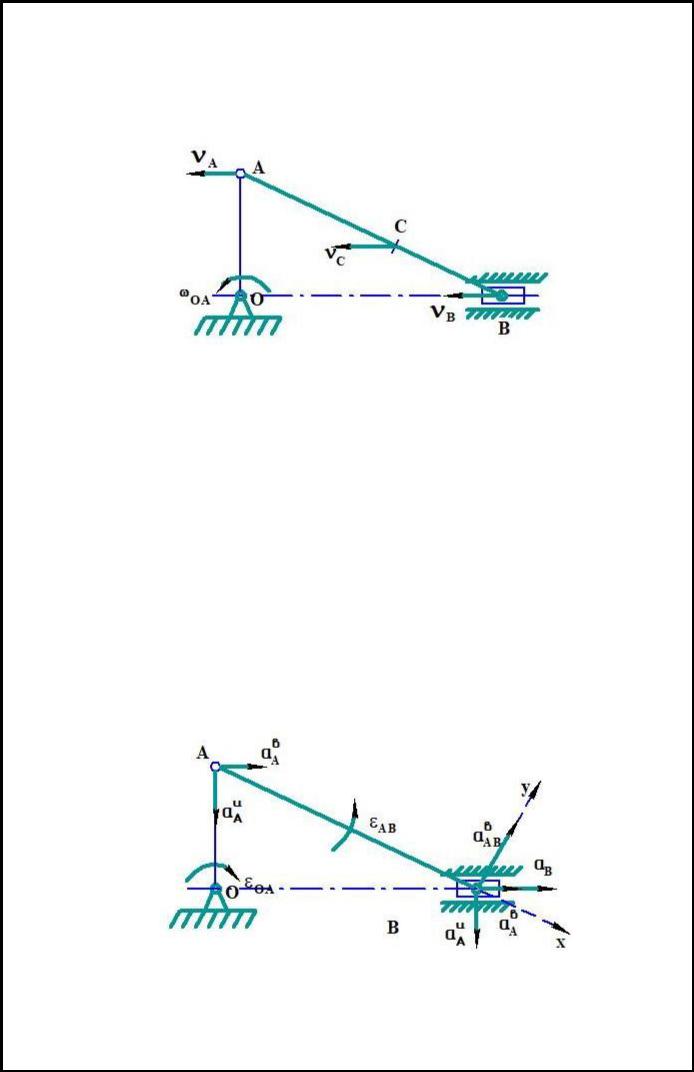
РЕШЕНИЕ:
1) Определение скоростей точек В и С и угловой скорости звена АВ.
Вычислим модуль скорости пальца А кривошипа ОА при заданном положении механизма
vA OA OA = 4 35=140 (см/с)
Вектор скорости т.А перпендикулярен ОА, направлен в сторону вращения
механизма.
Мгновенный центр скоростей находится в «бесконечности» и звено АВ
совершает |
в |
данный момент поступательное движение ( АВ 0 ), |
||
следовательно, скорости всех его точек одинаковы: |
||||
|
|
|
и |
vA vB vC 140 см/с. |
vA vB vC |
||||
2) |
Определение ускорений точек В и С и звена АВ. |
|||
Ускорение т.А складывается из вращательного и центростремительного
в ц
аА аА аА ;

Находим:
авА ОА ОА 8 35 280 (см/с)
ацА ОА2 ОА 42 35 560 (см/с)
Согласно теореме об ускорениях точек плоской фигуры
|
|
в |
ц |
или |
|
в |
ц |
в |
ц |
аВ аА аАВ аАВ |
аВ аА аА аАВ аАВ |
||||||||
Центростремительное ускорение т В во вращательном движении шатуна
АВ вокруг полюса А: |
|
|
|
|
|
|||
ацАВ АВ2 |
АВ 0 , |
так как АВ 0 . |
|
|
|
|
||
Вектор |
ц |
направлен от А к О. |
|
|
|
|
||
а |
А |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
Вектор |
в |
|
|
ц |
|
|
|
|
а А перпендикулярен вектору |
а А и направлен противоположно |
v A |
||||||
(вращение кривошипа ОА – замедленное). |
|
|
|
|||||
|
|
|
|
т.В и вращательного ускорения |
в |
шатуна известны |
||
Для ускорения аВ |
аАВ |
|||||||
только линии их действия: аВ - по горизонталь вдоль направляющих ползуна,
в - перпендикулярно АВ. Зададимся произвольно их направлениями по
аАВ
указанным линиям.
Проекции векторного равенства на оси координат:
аВ cos30 aвA cos30 aцA sin 30 ,
аВ sin 30 aвA sin 30 aцA cos30 aвAB .
Отсюда получаем
аВ авА ацА tg30 280 560  33 603,3 (см/с2),
33 603,3 (см/с2),
авАВ (аВ авА ) sin 30 ацА cos30 (603,3 280) 0,5 560 0,866 646,7 (см/с2).
|
|
|
|
|
|
|
|
Ускорения |
аВ |
и |
аАВв положительны, т.е их истинные направления |
||||
соответствуют принятым. |
|
|
|
|
|||
Угловое ускорение шатуна АВ определяется по формуле: АВ |
|
авАВ |
|
. |
|||
|
|
||||||
|
|
|
|||||
|
АВ |
|
|||||
|
|
|
|
|
|
|
|
Вначале определим длину шатуна АВ:
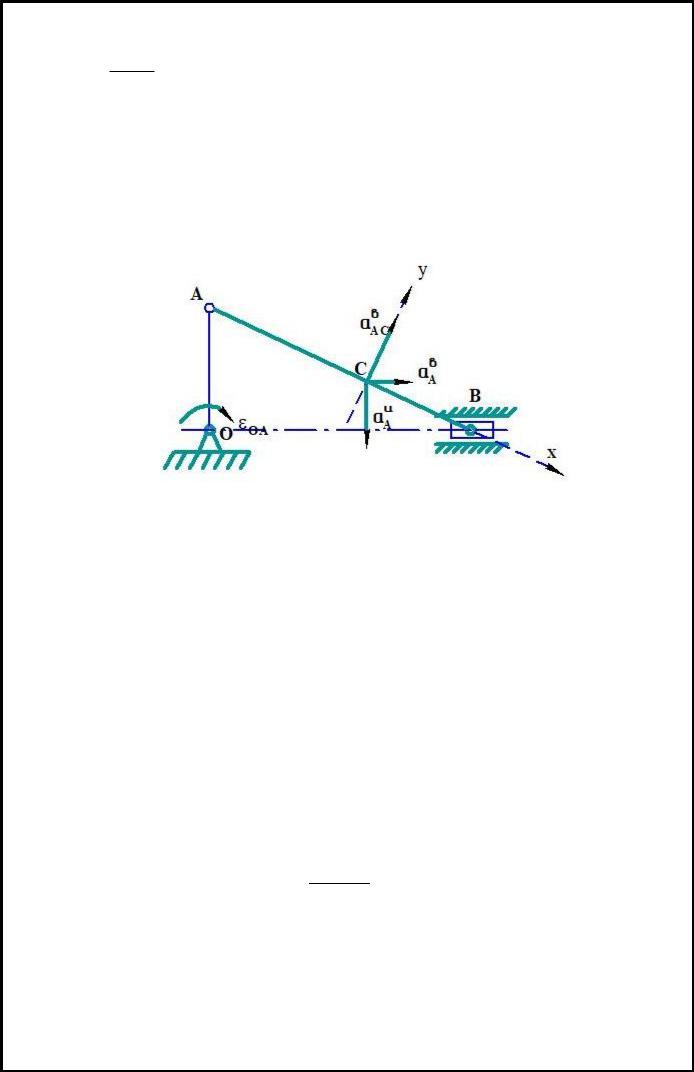
ОА |
|
АВ sin 30 |
2 OA 70 (см) |
Тогда АВ 646,7 / 70 9,24 (рад/с2)
Ускорение т.С определяем аналогично, как и для т.В:
|
|
в |
|
ц |
|
в |
|
ц |
а |
а |
а |
а |
а |
||||
С |
|
А |
|
А |
|
АС |
|
АС |
Вращательное и центростремительное ускорения т.С во вращательном
движении АВ вокруг полюса А
авАС АВ АС авАС 415,7 (см/с2) |
|
||
ац |
2 |
АС 0 |
|
АС |
АВ |
|
|
|
|
|
АВ |
Вектор |
аАСв направлен в соответствии с угловым ускорением |
||
перпендикулярно АС.
Ускорение т.С находим способом проекций, используя те же направления осей координат, что и для т.В:
аСх авА cos30 ацА sin 30 522,5 см/с2
аСy aвАC aвA sin 30 aцA cos30 70,7 см/с2
аС 
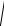 аСх2 аС2y 527,3 см/с2
аСх2 аС2y 527,3 см/с2
4. Определение кинематических характеристик точки в
сложном движении.
4.1 Основные сведения из теории кинематики сложного движения точки.
Движение точки по отношению к двум системам отсчета, из которых одна неподвижна (условно), а другая перемещается по отношению к неподвижной.
Такое движение точки называется сложным.
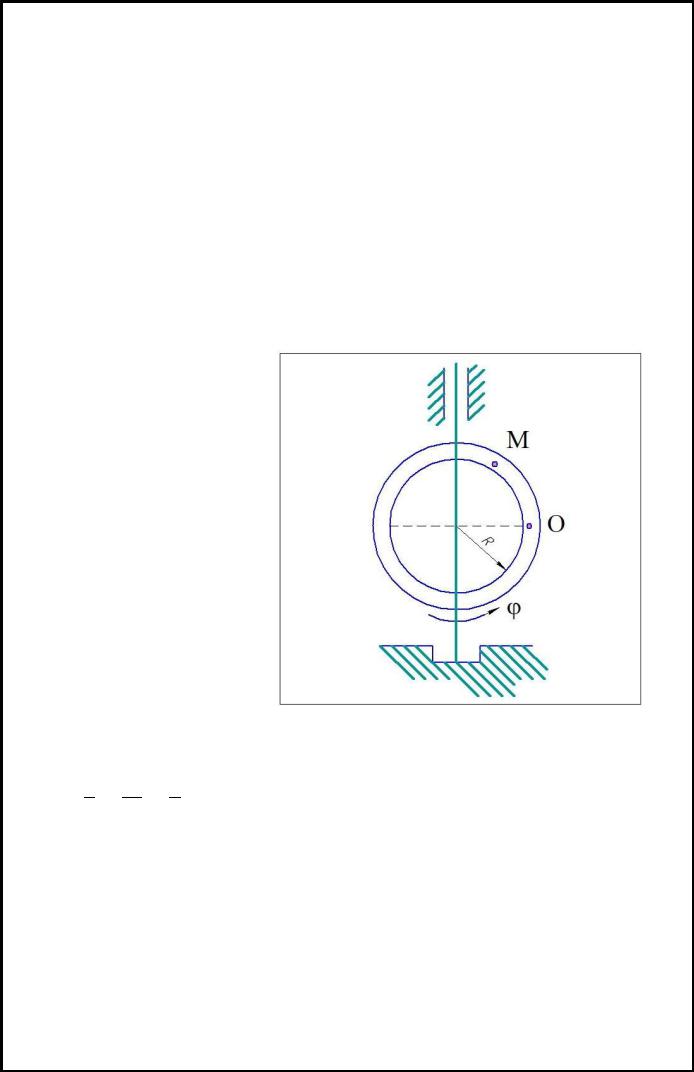
4.2 Задача К3 из (3).
Дано: Sr=OM(t)=5π(t2-3)см; φe=φ(t)=3t2-8tрад; R=20см; t=2с
Определить абсолютную скорость и абсолютное ускорение точки М в
Решение:
Точка М совершает слож-
ное движение, состоящее из переносного вращения вместе с кольцом и относи-
тельного движения по кольцу.
При t=2c имеем S=5π(t2-3)=5π (м), найдем центральный угол
Согласно теореме о сложении скоростей абсолютная скорость точки М равна векторной сумме относительной и переносной скоростей: = r+ e
Определяем r и e
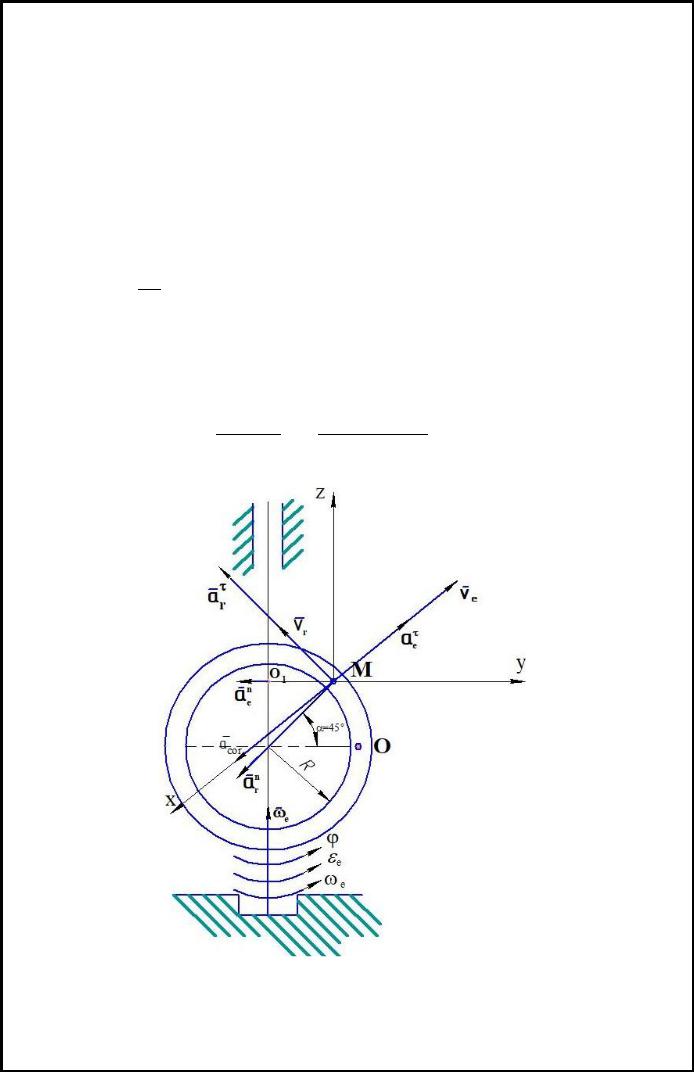
Относительная скорость:
Вектор r направлен по касательной к дуге.
Переносная скорость: e=ωe×MO1; MO1=Rcos α=20×0,707=14,1м
где
e=4×14,1=56,6м/с вектор e направлен перпендикулярно МО1
параллельно оси Х. Так как вектора r и e взаимно перпендикулярны, то

Абсолютное ускорение точки равно геометрической сумме относительного,
переносного и кориолисова ускорений: аа=аr+ae+acor
или в развернутом виде: аа=arτ+ arn+ aeτ+ aen acor
Модуль относительного касательного ускорения:
arτ =
Положительный знак у arτ показывает, что вектор ускорения arτ направлен в сторону положительных значений Sr.
Относительное нормальное ускорение:
Модуль переносного вращательного ускорения:
где εe – модуль углового ускорения кольца.
Вектор aeτ направлен перпендикулярно OM, параллельно оси Х.
Переносное центростремительное ускорение:
aеn=ωe2×MO1=42×14,1=225,6м/с2 аеn параллельно MO1
Ускорение Кориолиса: аcor=2ωe× r,

модуль acor=2ωeVr sin45˚=2×4×62,8×0,707=355,2м/с2
Направление определяем по правилу векторного произведения.
Проектируем на оси координат:
ax=acor-aeτ =335,2-84,6=270,6м/с2
ay= -aen-arn cos45˚-arτ cos45˚=-225,6-(197,2×0,707)-(31,4×0,707)=-387,2м/с2
az= -arn sin45˚+arτ sin45˚=-197,2×0,707+31,4×0,707=-117,2м/с2
aa=
5. Исследование динамики поступательного и вращательного
движения тел.
5.1 Основные сведения из теории: теоремы о движении центра масс и об изменении кинетического момента механической системы.
Теорема о движении центра масс звучит следующим образом: центр масс механической системы движется как материальная точка с массой равной массе всей системы, к которой приложены все внешние силы, действующие на систему.
Используя вышеописанные уравнения можно определять движение центра масс системы, не определяя движения отдельных ее точек.
Если в качестве механической системы рассматривать твердое тело,
то полученные выражения будут являться дифференциальными уравнениями поступательного движения данного тела. Поэтому поступательно движущееся тело можно рассматривать как материальную точку с массой, равной массе всего тела.
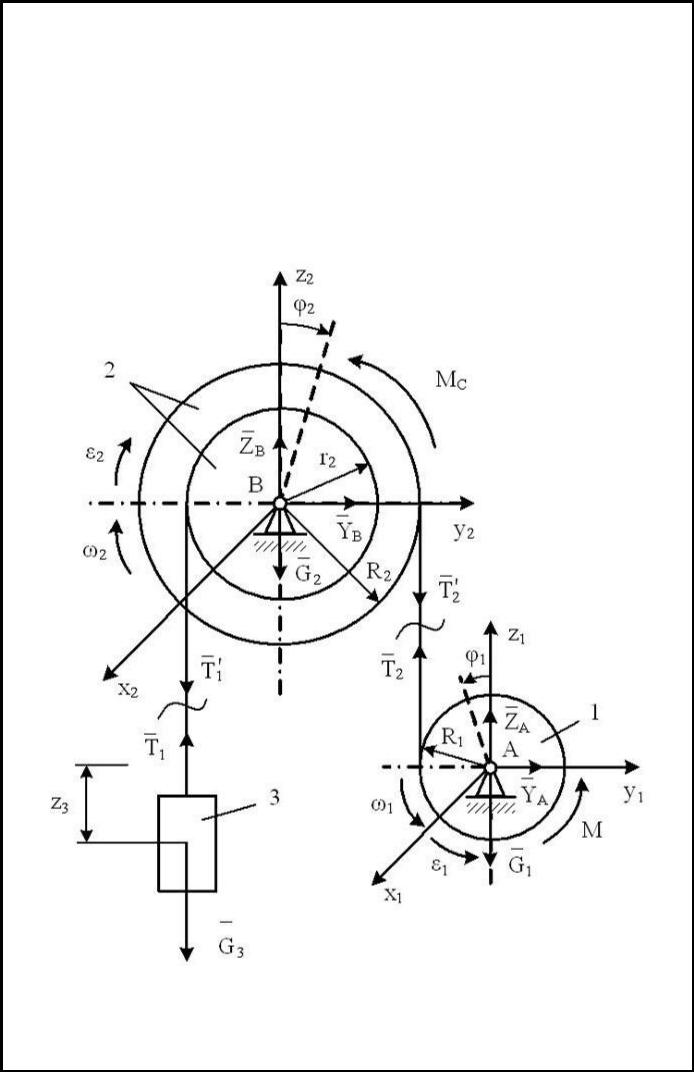
5.2. Задача Д 3 из (3). |
|
|
|
|
|
|
|
|
|
|||
Дано: m1 100 |
кг, m2 250 |
кг, m3 300 кг, |
R1 20 |
см 0,2 м, |
R2 50 |
см 0,5 м, |
||||||
r 30 см 0,3 |
м, i |
x2 |
40 |
см 0,4 м, M 1000 40t Нм, M |
C |
1400 Нм, |
|
1,5 с-1, |
||||
2 |
|
|
|
|
|
|
|
|
10 |
|
||
t1 2 с |
|
|
|
|
|
|
|
|
|
|
|
|
Найти: 1 (t) , T1 , T2 Решение:

В данной механической системе колеса 1 и 2 механизма вращаются вокруг неподвижных осей, а поднимаемый груз 3 совершает поступательное движение.
Напишем дифференциальные уравнения движения каждого из этих трех тел,
для чего отделим их друг от друга, разрезав соединительные нити.
На колесо 1 механизма действуют сила тяжести G1 , движущий момент М,
составляющие реакции опоры (YA и Z A ), сила натяжения нити T2 .
На колесо 2 действуют сила тяжести G2 , составляющие реакции опоры (YB и
Z B ), силы натяжения нитей (T1 и T2 ), момент сопротивления МС.
На груз 3 действуют сила тяжести G3 , сила натяжения нити T1 .
Очевидно, что T1 T1 и T2 T2 .
Составим дифференциальное уравнение вращения колеса 1 вокруг оси х1:
J x 1 М T2 R1 |
(1) |
1
Составим дифференциальное уравнение вращения колеса 2 вокруг оси х2:
J x2 2 T2 R2 T1r2 M C |
(2) |
Составим дифференциальное уравнение поступательного движения груза 3:
m3 z3 T1 G3 |
|
|
|
|
(3) |
|||
Колеса 1 и 2 связаны нитью, значит 1 R1 2 R2 |
||||||||
|
R1 |
|
|
0,2 |
|
|
|
|
Отсюда 2 1 R2 |
1 0,5 |
|||||||
0,4 1 , а значит 2 |
0,4 |
|||||||
Скорость груза 3: |
|
|
|
|
|
|||
v3 2 r2 0,4 1 0,3 0,12 1 |
, а значит z3 0,12 1 |
|||||||
|
|
|
|
|
|
|
|
|
Моменты инерции колес 1 и 2:

|
|
|
|
m R2 |
|
100 0,22 |
2 кг·м |
2 |
|
|
|
||||
J |
|
|
|
1 1 |
|
|
|
|
|
|
|||||
x1 |
|
|
2 |
2 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
J x2 |
m2i22x |
250 0,42 |
40 кг·м2 |
|
|
|
|||||||||
Из уравнения (3): |
|
|
|
|
|
|
|||||||||
T1 m3 z3 G3 300 0,12 1 300 9,8 36 1 2940 |
|
|
|||||||||||||
Из уравнения (2), с учетом того, что T1 T1 и T2 |
T2 : |
||||||||||||||
T2 |
|
J x |
2 |
T1r2 M C |
|
40 0,4 |
(36 2940) 0,3 1400 |
53,6 1 |
|||||||
|
|
|
2 |
|
|
|
|
1 |
1 |
|
|||||
|
|
|
|
R2 |
|
|
0,5 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
Подставим известные в уравнение (1):
(4)
4564 |
(5) |
21 1000 40t (53,61 4564) 0,2
21 1000 40t 10,721 912,8
12,721 87,2 40t
1 3,15t 6,86
Дважды интегрируем:
1 1,575t 2 6,86t C1
1 0,525t 3 3,43t 2 C1t C2
Используем начальные условия: при t0 0 10 0 и 10 10 1,5 рад/с
Тогда
C1 10 1,575t02 6,86t0 1,5 1,575 02 6,86 0 1,5 рад/с
C2 10 0,525t03 3,43t02 C1t0 0 0,525 03 3,43 02 1,5 0 0
Уравнение угловой скорости колеса 1 принимает вид:
1 1,575t 2 6,86t 1,5 (рад/с)
