Курсовая / Отчет по курсовику

-15.0000 -10.0000 -5.0000 -4.0000 -3.0000 -2.0000 -1.0000

Замкнутая линейная система с динамическим регулятором устойчива и имеет желаемые собственные значения системы и наблюдателя.

Таким образом, неустойчивый объект и неустойчивый регулятор образуют устойчивую систему с отрицательной обратной связью.

3.4. Оценка области притяжения положения равновесия

Устойчивость линейной модели означает устойчивость «в малом» положения равновесия нелинейной системы (первый метод Ляпунова). Другими словами, существует область притяжения положения равновесия.

Подключим динамический регулятор к нелинейному объекту (рис.

3.1).

21

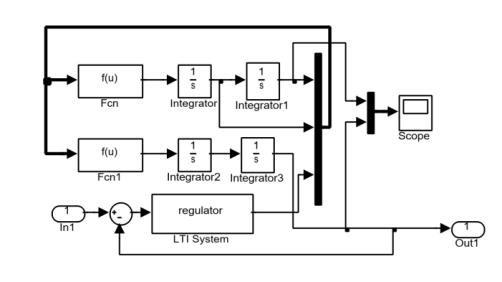
Рис 3.1. Система «нелинейный объект + динамический регулятор»

Для нелинейной системы (см. рис. 3.1) проведем проверку выполнения условия устойчивости «в малом». Линеаризуем замкнутую систему и вычислим собственные значения:

>>[Ac,Bc,Cc,Dc]=linmod2('pendulum');

>>eig(Ac)

ans = -20.0000 -15.0000 -10.0000 -1.0000 -5.0000 -2.0000 -4.0000 -3.0000

22

Получены те же собственные значения. Таким образом, существует область устойчивости — положение равновесия нелинейной системы управления устойчиво «в малом».

Вместе с тем, для практики важно знание размеров области притяжения положения равновесия (устойчивость «в большом»).

Для нелинейных моделей нет расчетных методов оценки размеров области притяжения. Единственным способом приближенной оценки является многократное компьютерное моделирование при различных начальных условиях.

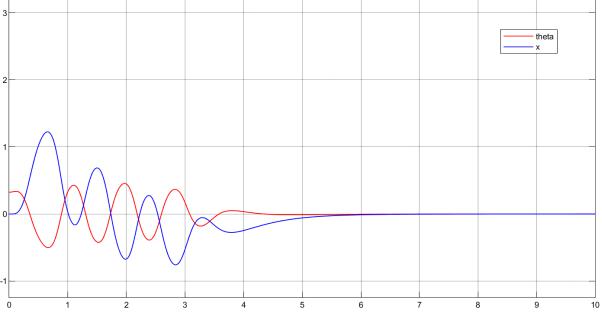
Для примера на рис. 3.2. приведен результат такого поиска — процессы при максимальном отклонении маятника на 0.3246 радиана от положения равновесия. Линейный динамический регулятор способен стабилизировать нелинейный объект.

Рис. 3.2. Поведение системы при максимальном начальном отклонении маятника на 0.3246 рад

На рис. 3.3. приведен результат при максимальном отклонении каретки на 0.0123 радиана от положения равновесия. Линейный динамический регулятор способен стабилизировать нелинейный объект.

23

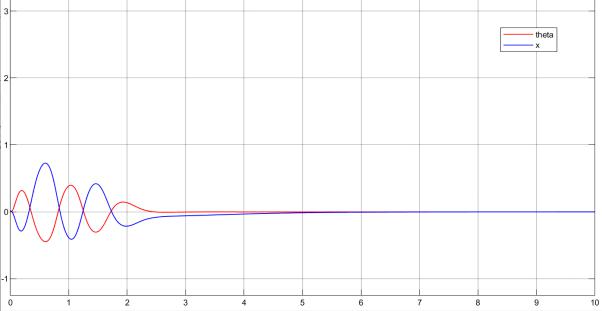
Рис. 3.3. Поведение системы при максимальном начальном отклонении

каретки на 0.0123 рад

24

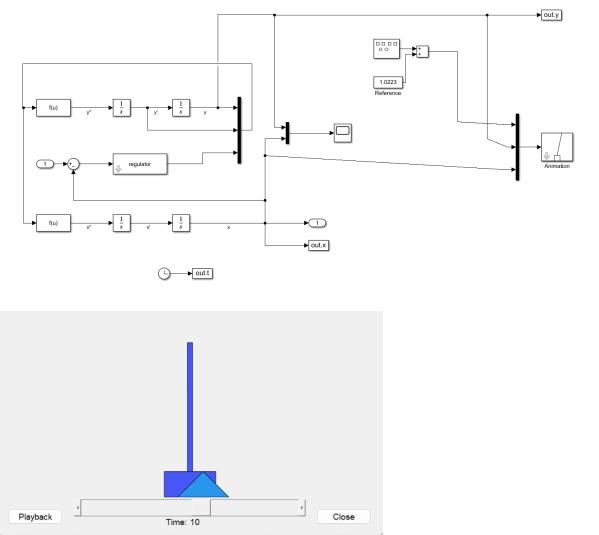
3.5. Упрощенная анимация системы управления

Рис. 3.4. Упрощенная анимация системы управления

25

4. СИНТЕЗ СИСТЕМ РЕГУЛИРОВАНИЯ ОПЕРАТОРНЫМ МЕТОДОМ

4.1. Операторный метод размещения корней характеристического полинома системы

Допустим, что требования к системе представлены в форме желаемого множества корней характеристического полинома (ХП). Необходимо найти алгоритм регулятора, размещающего корни в назначенных местах комплексной плоскости.

Запишем дифференциальное уравнение объекта в операторной форме:

Положим, что степень 0 полинома 0 выше степени 0 полинома

0. Кроме того, допустим, что полиномы 0 и 0 взаимно просты, т.е.

описание вход-выход объекта (4.1) является полным.

Искомое дифференциальное уравнение регулятора также запишем в операторной форме

где:

( ) = + + 1 + 0 ;

( ) = + + 1 + 0 ;

Дифференциальное уравнение замкнутой системы получим, если исключим переменную u(t) из уравнений (4.1) и (4.2):

( ) ( ) = [ ( ) ( ) + ( ) ( )] ( ) = 0 (4. 3)

3 0 0

, где выражение в квадратных скобках — ХП системы.

26

Назначим желаемые корни ХП системы * ; = 1,..., : и построим желаемый полином:

Из тождества (4.5) необходимо найти операторные полиномы регулятора ( ) и ( ).

Без потери общности примем, что коэффициенты при старших степенях полиномов 0( ) и 0( ) равны единице; следовательно,

старший коэффициент полинома 3 также равен единице.

Задача решается в два этапа.

1. Находятся степени и операторных полиномов (структура регулятора). Для упрощения примем = . Тогда число неизвестных параметров регулятора равно 2 + 1.

Степень полинома 3 равна сумме степеней полиномов 0 и , т. е.

порядок системы равен сумме порядков объекта и регулятора. Такой же

должна быть и степень желаемого характеристического полинома * . Таким образом, из тождества (4.5) следует 0 + уравнений.

Число неизвестных параметров регулятора должно равняться числу уравнений:

2 + 1 = 0 + ;

откуда получим порядок регулятора:

27

2. Вычисляются коэффициенты полиномов (параметры регулятора). Порядок дифференциального уравнения системы регулирования равен:

= 0 + = 2 0 − 1;

таково же и число искомых параметров регулятора.

Записывается система уравнений относительно искомых параметров.

4.2. Пример стабилизации перевернутого маятника на закрепленной каретке

Малые отклонения маятника от верхнего положения равновесия описываются дифференциальным уравнением второго порядка:

( 2 − 1) ( ) = ( ),

где: u — управляющее воздействие. Для простоты принято, что значение l

— длины маятника численно равно значению g — ускорения силы тяжести.

Один из корней 1,2 =± 1 ХП дифференциального уравнения объекта положителен.

Порядок объекта равняется двум ( 0 = 2). Из (4.6) найдем порядок дифференциального уравнения регулятора: = 1. Следовательно,

необходимо определить три коэффициента дифференциального уравнения первого порядка:

( + ) ( ) =− ( + ) ( ).

0 1 0

Порядок системы равен трем. Назначим три желаемых корня:

*1 =− 1; *2 =− 2; *3 =− 4 (один из корней ХП объекта оставляем на месте).

28

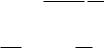
ХП замкнутой системы в соответствии с (4.3) имеет вид:

3( ) ≡ ( 2 − 1)( + 0) + 1 · ( 1 + 0) =

= 3 + 0 2 + ( 1 − 1) + ( 0 − 0)

Сформируем в соответствии с (4.4) желаемый ХП

*( ) = ( + 1)( + 2)( + 4) = 3 + 7 2 + 14 + 8

Из тождества 3( ) и *( ) получим систему уравнений:

0 = 71 − 1 = 14

0 − 0 = 8

решая которую получим искомые коэффициенты регулятора, обеспечивающего заданное расположение корней:

0 = 7; 1 = 15; 0 = 15

4.3. Пример маятника на подвижной каретке

Ранее получены полиномы знаменателя (2.5) и числителя (2.6) ПФ объекта от управляющего воздействия f до положения каретки x. Запишем дифференциальное уравнение объекта в операторной форме:

0( ) ( ) = 0( ) ( ),

. где:

0( ) = 1 ( 2 − 1 ).

Численные значения коэффициентов полиномов ПФ для заданных параметров объекта (l = 1; m = 0.1; M = 0.5) равны:

29

0( ) = 4 − 11. 76 2; 0( ) = 2( 2 − 9. 8) = 2 2 − 19. 6

Структурный синтез — определение порядка регулятора — сводится к анализу степеней операторных полиномов. Степени полиномов объекта0, 0 равны соответственно: 0 = 4, 0 = 2 . Порядок регулятора равен

трем = = 0 − 1 = 4 − 1 = 3. Таким образом, порядок системы равен семи = 0 + = 4 + 3 = 7 .

Искомое дифференциальное уравнение стабилизирующей отрицательной обратной связи (регулятора) также запишем в операторной форме:

( ) ( ) = − ( ) ( )

В раскрытом виде с учетом степеней полиномов , получим:

( 3 + 2 + + ) ( ) = ( 3 + 2 + + ) ( )

2 1 0 3 2 1 0

Параметрический синтез сводится к вычислению семи коэффициентов дифференциального уравнения регулятора.

Поскольку порядок системы равен семи, назначим семь желаемых корней в левой полуплоскости:

* = − 1; − 2; − 3; − 5; − 10; − 15; − 20.

Ориентируемся на корни ХП объекта, причем, устойчивый корень ХП объекта оставляем на месте.

Желаемый ХП построим с помощью команд MATLAB. Вводим желаемые корни:

>> r = [− 1; − 2; − 3; − 4; − 10; − 15; − 20];

и вычисляем коэффициенты полинома по команде

>> poly(r) ans =

30