Курсовая / Отчет по курсовику

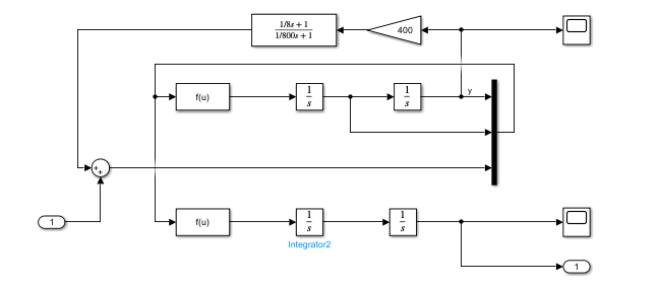
следствие высокой частоты среза система оказывается быстродействующей).

Создадим simulink-модель нелинейной системы с замкнутым контуром стабилизации маятника с именем 'linear_pend_1' (рис. 5.2).

Рис. 5.2. Модель нелинейной системы стабилизации маятника

Проведем анализ устойчивости системы стабилизации положения маятника — преобразуем модель к форме пространства состояний

>> [A1,B1,C1,D1]=linmodv5('linear_pend_1' ');

и вычислим собственные значения

>> eig(A1) ans =

0

0 -8.6183 -106.8944 -684.4873

41

Два нулевых собственных значения остались на месте. Они принадлежат неуправляемой части объекта — состоянию каретки.

2. Второй этап синтеза ― стабилизация положения каретки (с маятником). Управляемым объектом (второго уровня) синтеза оказывается система, синтезированная на первом этапе (рис. 5.2). Ее входом, как и на первом этапе, является сила f, действующая на каретку, а выходом ― положение каретки x.

Вычислим ПФ объекта второго уровня: >> plant1=ss(A1,B1,C1,D1);

или в факторизованном виде

>> zpk(plant1)

2 (s+800) (s+3.132) (s-3.132)

---------------------------------

s^2 (s+8.618) (s+106.9) (s+684.5)

ПФ не имеет одинаковых нулей и полюсов (объект является полностью управляемым и наблюдаемым).

ПФ имеет положительный нуль 2 = 3. 132, т. е. является

неминимально-фазовой. Это свидетельствует о том, что объект второго уровня имеет отрицательный коэффициент усиления (точнее, добротность).

Известно, что корни ХП замкнутой системы стремятся к нулям разомкнутой системы, модули которых принадлежат диапазону частот, где велико усиление контура. Наличие у ПФ правого нуля требует, чтобы на этой частоте усиление контура было малым. Следовательно, на частоте2 3. 132 рад/с усиление желаемого контура должно быть не более

42

–16…–20 дБ. Тогда замкнутая система не будет иметь собственных значений, близких к правому нулю ПФ объекта второго уровня.

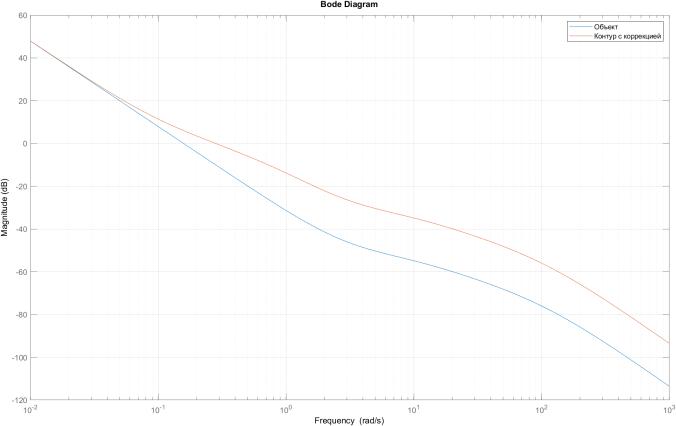
Частотная характеристика объекта второго уровня приведена на рис. 5.3 (синяя кривая “Объект”). Низкочастотная асимптота ЛАЧХ с наклоном –40 дБ/дек пересекает ось 0 дБ на частоте среза, примерно равной 0.2 рад/с.

Рис. 5.3. ЛАЧХ второго этапа синтеза: объекта (синяя); контура после коррекции (оранжевая)

Дополнительным условием, накладываемым на желаемую ЛАЧХ контура второй подсистемы, является малое усиление на частотах корней, сформированных на первом этапе. Усиление контура должно быть менее –16…–20 дБ на определенных частотах. Таким образом, желаемая ЛАЧХ типового вида должна проходить ниже этих контрольных точек, что обеспечивает соблюдение обоих ранее оговоренных условий.

43

Очевидно, достаточно контролировать только низшую из перечисленных частот. Это требование автономности подсистем также ограничивает полосу пропускания частот контура, а соответственно и быстродействие системы стабилизации каретки.

Далее действуем аналогично процедуре синтеза первого контура. Включим активную последовательную коррекцию с ПФ: >>corr1=tf([11.24 1],[1.12 1])

т. е. введем в контур действительный нуль 3 = –11. 24 и полюс

3 = –1. 12, что дает типовую ЛАЧХ с отрезком асимптоты с наклоном

−20 дБ/дек в окрестности частоты среза на рис. 5.3 (оранжевая кривая “Контур с коррекцией”).

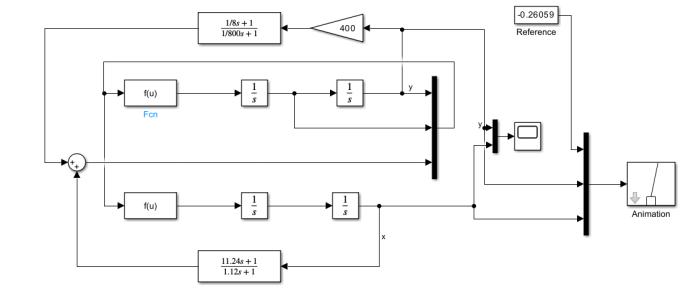
Создадим simulink-модель системы с замкнутым контуром стабилизации каретки 'pend_2' (рис. 5.4). Обратим внимание на сумматоры, в которых сигналы обратных связей суммируются со знаком «+». Это следствие неминимально-фазовой ПФ объекта.

Рис. 5.4. Структурная схема системы стабилизации 'pend_2', образованная двумя регуляторами

44

Для анализа устойчивости системы преобразуем модель к форме пространства состояний:

>> [A2,B2,C2,D2]=linmod2(‘pend_2');

и вычислим собственные значения:

>>eig(A2) ans =

1.0e+02 *

-6.8448 -1.0714 -0.0839

-0.0035 + 0.0007i -0.0035 - 0.0007i -0.0018

Получилась устойчивая «в малом» система шестого порядка. Большой разброс собственных значений приводит к сильно различающимся по темпу процессам стабилизации маятника и каретки.

Ввиду относительной малости постоянных времени знаменателей ПФ можно полагать, что для стабилизации приняты ПД-регуляторы:

- для маятника 400*(0.125 s + 1)/(0.00125 s + 1), -для каретки (11.24 s + 1)/(1.12 s + 1).

Свойство неполной наблюдаемости маятника на каретке по выходу ― угловому положению маятника — позволило реализовать декомпозицию процедуры синтеза. Вначале синтезируется стабилизирующая обратная связь для маятника, после чего находится регулятор положения каретки. Ограничения, обеспечивающие условия приближенной автономности подсистем стабилизации маятника и

45

каретки, естественным образом учитываются благодаря частотному подходу. Важнейшей особенностью частотного подхода является учет динамики объекта (нескорректированного контура) при выборе желаемого поведения, т. е. желаемой частотной характеристики.

Посмотрим на работу полученного контура.

Рис 5.5. Максимальный начальный угол отклонения маятника

0 = 1. 565 рад = 89. 67 градусов;

46

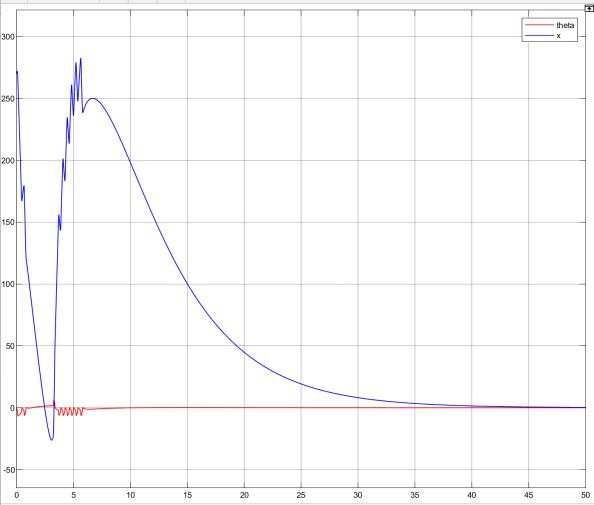
Рис 5.6. Максимальное отклонение маятника на 0 = 269. 89 м;

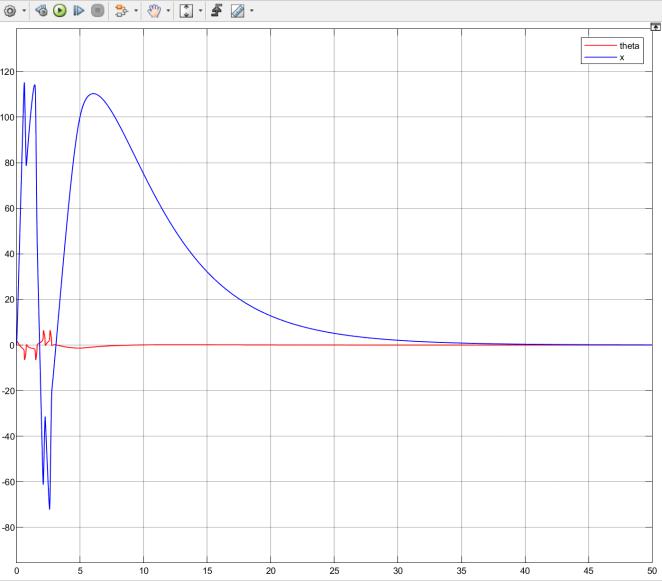
Теперь посмотрим на систему в работе при реальных начальных условиях ( 0 = 0. 15, 0 = 0. 1) рис 5. 7:

47

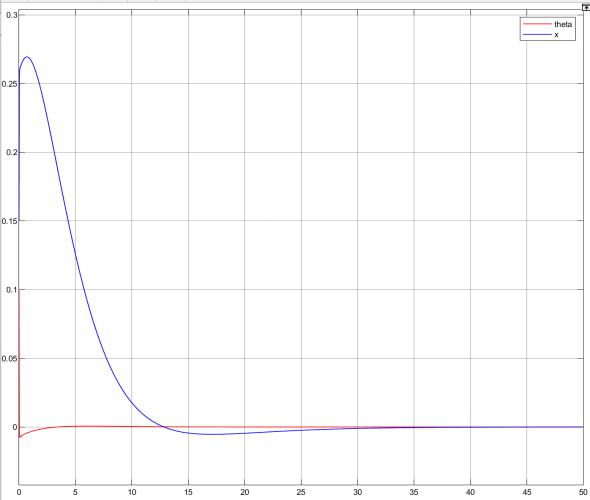
Рис 5.7. Система в работе при 0 = 0. 15, 0 = 0. 1

. 6. СИСТЕМЫ С ЦИФРОВЫМИ УПРАВЛЯЮЩИМИ

УСТРОЙСТВАМИ

6.1. Модели систем цифрового управления непрерывными объектами

Дискретизация времени и квантование уровней сигналов в большинстве современных систем управления обусловлена применением цифровых управляющих устройств. Принципиальная схема системы цифрового управления непрерывным объектом изображена на рис. 6.1.

48

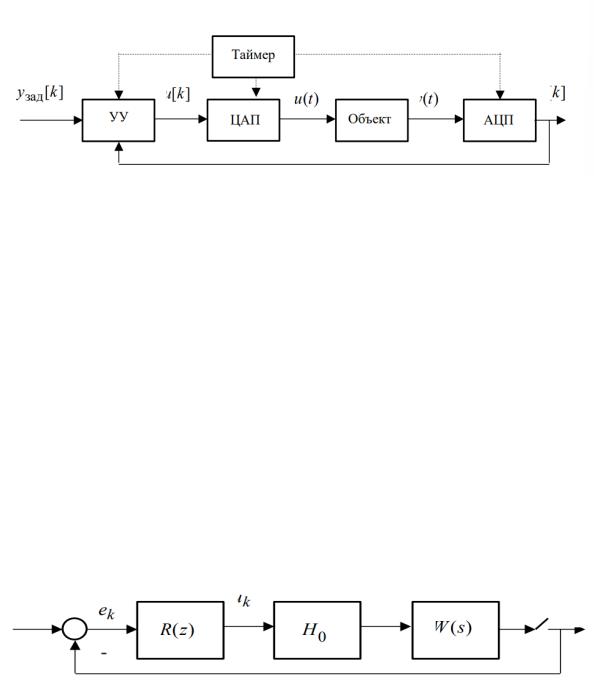
Рис.6.1. Система цифрового управления непрерывным объектом

Динамика непрерывного объекта описывается дифференциальными уравнениями и/или ПФ ( ) .

Цифровое управляющее устройство (УУ) описывается разностными уравнениями и/или дискретной ПФ ( ), равной отношению Z-изображений ( ) и ( ), где ( )- изображение ошибки системы.

Модель системы (рис. 6.2) оказывается неоднородной (гибридной), так как она образована разнородными элементами, а переносимая между ними информация кодируется различными типами сигналов:

аналоговыми , и с дискретным временем − , , .

Рис. 6.2. Структурная схема системы цифрового управления

Разнородные компоненты системы взаимодействуют с помощью интерфейса, роль которого играют аналого-цифровой и цифроаналоговый преобразователи (АЦП и ЦАП). Как правило, АЦП выполняет измерительные, а ЦАП — исполнительные функции.

49

Работа АЦП и ЦАП должна быть синхронизирована; они имеют дополнительные входы для сигнала таймера (см. рис. 6.1).

АЦП содержат квантизаторы уровня, в которых число уровней определяется длиной машинного слова. Если мощность множества значений сигнала велика, как это бывает в современных компьютерах, то квантованием уровня в большинстве случаев моделирования можно пренебречь.

Примем, что моделью АЦП является так называемый «ключ», который периодически замыкается на пренебрежимо малое (по сравнению со скоростью изменения переменной) время. Ключ позволяет получать информацию о переменной ошибки в равноотстоящие моменты времени:

= [ ] = ( ); = 0, , 2 , ... ;

T - период дискретизации времени (англ. Ts - Sampling Time - время выборки).

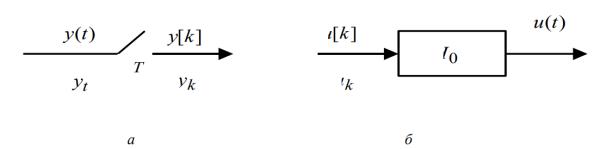
Рис. 6.3. Примеры графических изображений: дискретизатор времени непрерывного сигнала («ключ»)(а); фиксирующее устройство (б)

ЦАП - другая часть интерфейса между непрерывной и цифровой частями - до поступления новой информации от УУ экстраполирует значения управляющего воздействия на объект ( ) .

Простейший и часто применяют экстраполятор нулевого порядка 0

(фиксатор) сохраняет предыдущее значение сигнала управления:

50